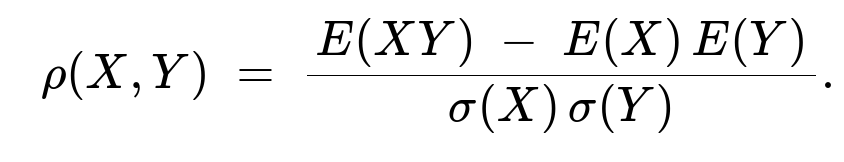ML Interview Q Series: Calculating Correlation Coefficient Using a Joint Probability Density Function
Browse all the Probability Interview Questions here.
The continuous random variables (X) and (Y) have the joint density function
[ \huge f(x, y) ;=; 6,\bigl(x - y\bigr) \quad\text{for }0 < y < x < 1, ] and (f(x,y) = 0) otherwise. Determine the correlation coefficient of (X) and (Y).
Short Compact solution
From the given joint pdf (f(x,y) = 6,\bigl(x - y\bigr)) on the region (0 < y < x < 1), one finds the marginal density of (X) by integrating out (y):
(f_X(x) = 6 \int_{y=0}^{x} (x - y),dy = 3,x^2 \quad\text{for }0 < x < 1.)
Similarly, the marginal density of (Y) is obtained by integrating out (x):
(f_Y(y) = 6 \int_{x=y}^{1} (x - y),dx = 3y^2 ;-;6y ;+;3 \quad\text{for }0 < y < 1.)
These lead to:
(E(X) = 3/4.)
(\sigma(X) = \tfrac{1}{4}\sqrt{3}.)
(E(Y) = 1/4.)
(\sigma(Y) = \sqrt{3/80}.)
Furthermore,
(E(XY) = 6 \int_{x=0}^{1} \int_{y=0}^{x} x,y,(x - y),dy,dx = 1/5.)
Hence, using the standard formula for the correlation coefficient,
we substitute the values:
Numerator: (E(XY) - E(X)E(Y) = \tfrac{1}{5} ;-; \bigl(\tfrac{3}{4}\bigr)\bigl(\tfrac{1}{4}\bigr) = \tfrac{1}{5} - \tfrac{3}{16}.)
Denominator: (\bigl(\tfrac{1}{4}\sqrt{3}\bigr),\sqrt{\tfrac{3}{80}}.)
The result is approximately (0.1491.)
Comprehensive Explanation
Joint PDF and Region of Support
The joint pdf is given by (f(x,y) = 6,(x - y)) on the region (0 < y < x < 1). Geometrically, this corresponds to the triangular region in the unit square where the vertical coordinate (y) is less than the horizontal coordinate (x). Outside this region, the density is zero.
To find expectations such as (E(X), E(Y),) and (E(XY)), one integrates over this triangular domain:
[
\huge 0 ;<; y ;<; x ;<; 1. ]
Marginal Distributions
Marginal of (X)
We integrate out (y): [ \huge f_X(x) ;=; \int_{y=0}^{x} 6,(x - y),dy \quad\text{for};0 < x < 1. ] Carrying out the integral yields [ \huge f_X(x) ;=; 3,x^2,\quad 0 < x < 1. ]
Marginal of (Y)
We integrate out (x): [ \huge f_Y(y) ;=; \int_{x=y}^{1} 6,(x - y),dx \quad\text{for};0 < y < 1. ] This evaluates to [ \huge f_Y(y) ;=; 3y^2 - 6y + 3,\quad 0 < y < 1. ]
Means and Standard Deviations
Once we have (f_X(x)) and (f_Y(y)), we can compute:
(E(X) = \int_{0}^{1} x,f_X(x),dx.)
(E(Y) = \int_{0}^{1} y,f_Y(y),dy.)
(\sigma(X)) comes from (\sqrt{,E(X^2) - \bigl(E(X)\bigr)^2,}).
(\sigma(Y)) comes from (\sqrt{,E(Y^2) - \bigl(E(Y)\bigr)^2,}).
In the short solution above, these are quoted as
(E(X) = 3/4,\quad \sigma(X) = (1/4)\sqrt{3}.)
(E(Y) = 1/4,\quad \sigma(Y) = \sqrt{3/80}.)
Computing (E(XY))
To find (E(XY)), we do the double integral of (x y f(x,y)) over the region:
[
\huge E(XY) ;=; \int_{0}^{1} !!!\int_{0}^{x} x,y,[6,(x - y)],dy,dx. ]
It simplifies to (1/5) (i.e., (0.2)) after careful integration, as stated in the short solution.
Correlation Coefficient
With
(E(XY) = 1/5,)
(E(X) = 3/4,)
(E(Y) = 1/4,)
(\sigma(X) = \tfrac{1}{4}\sqrt{3},)
(\sigma(Y) = \sqrt{\tfrac{3}{80}},)
the correlation coefficient (\rho(X,Y)) is given by
Substituting:
Numerator = (0.2 ;-; \bigl(0.75 \times 0.25\bigr) = 0.2 - 0.1875 = 0.0125.)
Denominator = (\Bigl(\tfrac{1}{4}\sqrt{3}\Bigr),\sqrt{\tfrac{3}{80}} \approx 0.0839.)
Hence,
[ \huge \rho(X,Y) ;\approx; 0.0125 ;\Big/; 0.0839 ;\approx; 0.149. ]
Potential Follow-up Questions
How does one interpret a correlation of around 0.15?
A correlation coefficient near 0.15 indicates a weak positive linear relationship between (X) and (Y). In practical data-analysis terms, while (X) and (Y) do tend to increase together slightly, the linear association is not very strong.
Could the sign of the correlation have been negative?
Yes, in principle. If the joint distribution had placed higher probability mass where (x) and (y) moved in opposite directions, we could have ended up with a negative covariance and hence a negative correlation. The sign and magnitude come directly from the integrals of (xy) and from how the density (f(x,y)) is arranged over the region.
Why do we use (E(XY)) instead of (\int x,dx,\int y,dy) for covariance?
Covariance (and correlation) crucially depends on the combined relationship of (X) and (Y). Simply multiplying the separate expectations (E(X)) and (E(Y)) would ignore how (X) and (Y) jointly vary in the same region of the sample space. The term (E(XY)) is precisely what captures the interaction of the two variables together.
How might one compute this in a programming language like Python?
A direct approach in Python might use symbolic integration tools (e.g., Sympy) for the continuous case. For a rough numerical check, one could do:
import numpy as np
N = 10_000_000
xs = np.random.rand(N)
ys = np.random.rand(N)
# Keep only those samples where y < x
mask = (ys < xs)
xs, ys = xs[mask], ys[mask]
# Weight factor, since we only want region 0<y<x<1 with pdf = 6(x-y)
# The uniform random draws in [0,1]^2 that satisfy y<x is half the square,
# so we scale the samples by the pdf 6(x-y) / Probability_of_region
# Probability_of_region is 1/2 for y<x in the unit square.
weights = 6*(xs - ys) / 0.5 # i.e. multiply by 2
# Estimate E(X) numerically
E_X = np.average(xs, weights=weights)
# Similarly E(Y)
E_Y = np.average(ys, weights=weights)
# Then E(XY)
E_XY = np.average(xs*ys, weights=weights)
# Then compute correlation:
cov_XY = E_XY - E_X*E_Y
# We can also approximate E(X^2), E(Y^2) to get Var(X), Var(Y).
Though one must be careful with weighting and normalizing for a proper Monte Carlo estimate. In practice, for large N, the results should approximate the true integrals.
How does correlation help in modeling or machine learning tasks?
In many ML problems, correlation is an initial indicator of linear association, helpful for feature selection or exploratory data analysis. However, it does not capture nonlinear relationships. For more complex dependencies, one often looks at mutual information or more sophisticated measures. But correlation remains a fundamental statistic for quickly summarizing linear dependence in data.
Could we have a different measure of dependence aside from correlation?
Yes. Correlation only captures linear dependence. For nonlinear relationships, measures like Spearman’s rank correlation or mutual information can capture broader forms of dependence. In higher-dimensional problems or where the relationship is not linear, relying solely on correlation can be misleading.
Would the correlation change if we shifted or scaled the random variables?
Scaling (X) or (Y) (multiplying by a positive constant) affects covariance but also affects each variable’s standard deviation in the same proportion, so the correlation coefficient (which is dimensionless) remains unchanged. Shifting (X) or (Y) (adding a constant) does not change correlation either, because correlation depends on centered variations around the mean.
Below are additional follow-up questions
If X and Y had a different support, say 0 < x < y < 1, how would we modify the analysis?
In this situation, the region of integration would flip, and the joint pdf would have to be appropriately defined on the new domain 0 < x < y < 1. This means:
The condition y < x would become x < y.
The integrals for the marginals would reflect the fact that for each y, x runs from 0 to y (instead of for each x, y runs from 0 to x).
If we retained the exact same formula 6(x - y) in that domain, we would see it could produce negative values where x < y, which is not permissible for a pdf. Hence, the form of the density would typically need changing.
A critical pitfall is that one must check whether the pdf remains nonnegative everywhere in the intended region. If x - y is negative whenever x < y, the density 6(x - y) would become invalid unless carefully adjusted (e.g., 6(y - x)). Also, the normalizing constant could differ. So the primary steps are:
Confirm positivity of the pdf on the new region.
Recompute all integrals (marginals, expectations) on the modified domain 0 < x < y < 1.
Ensure the integral of the pdf over that region is 1.
This highlights the subtlety that flipping the domain is not merely a matter of swapping x and y in the integration limits; it can invalidate the pdf if we don’t adjust the function accordingly.
What if we suspect a nonlinear dependence between X and Y despite the given correlation being small?
Correlation measures only the linear association between two variables. A small correlation (like 0.15) can obscure a nonlinear dependence. For instance, if the relationship were shaped like a parabola, the correlation might misleadingly be near zero even though there is a strong curvilinear trend.
In practice, to detect nonlinearities:
One might plot X vs Y (if it is feasible) to look for patterns that are curved, U-shaped, or otherwise non-linear.
Calculate higher-order statistics or use nonparametric measures like Spearman’s rank correlation or Kendall’s tau, which can detect monotonic relationships even if they’re nonlinear.
Employ kernel-based tests or mutual information estimates to capture broader dependencies.
A key pitfall is assuming near-zero correlation implies independence. In fact, X and Y can be very much dependent in a nonlinear sense while still having near-zero correlation.
How would you verify that 6(x - y) is a valid pdf on 0 < y < x < 1?
To confirm validity of any candidate joint pdf on a region, you must check two things:
Nonnegativity: 6(x - y) must be >= 0 on the domain. Since 0 < y < x < 1, we have x - y > 0, so 6(x - y) is indeed positive in that region.
Proper normalization: The integral of 6(x - y) over 0 < y < x < 1 must be 1. Concretely,
Integrate with respect to y from 0 to x, then integrate with respect to x from 0 to 1: [ \huge \int_{x=0}^1 \int_{y=0}^x 6 (x - y), dy , dx ;=; 1. ] By explicitly doing the calculation, you confirm the total integral is 1.
A common pitfall is forgetting to check these conditions when given a formula. A pdf that integrates to something different from 1 is not valid unless you rescale by the appropriate constant. Similarly, if part of the region yields negative values, that invalidates it as a pdf.
Could the correlation become undefined if the variance of X or Y were 0?
Yes. The correlation coefficient formula, E(XY) - E(X)E(Y)
sigma(X)*sigma(Y) becomes undefined if either sigma(X) = 0 or sigma(Y) = 0. A variance of zero implies that the variable takes on a single value with probability 1 (i.e., it is almost surely constant). In such a case, the correlation is mathematically undefined, because you would be dividing by zero.
Pitfalls include:
In real data scenarios, if one variable has negligible variance (for instance, a sensor that saturates or never changes), correlation computations can break down or produce NaN values.
A more general best practice is to always check the variance of your features before computing correlation to avoid meaningless outputs.
How would you handle the scenario if part of the domain yields negative values for x - y under the same formula?
If the pdf is stated as 6(x - y) but the region inadvertently extends to areas where x < y, you get negative pdf values, which is invalid. You would then need to:
Either restrict the domain strictly to ensure x > y, which the problem does (0 < y < x < 1).
Or modify the function so that it is nonnegative throughout the intended region, for example using an absolute value 6|x - y|, but that changes the integral and requires a different normalization factor.
A subtle but common error in constructing such problems is failing to align the piecewise definition of the pdf with the sign constraints. If you see a negative region, you might have missed a crucial piece in the domain specification or the pdf’s piecewise structure.
In practice, how might floating-point precision issues affect numerical estimates of correlation for such a distribution?
When computing the integrals numerically (e.g., via Monte Carlo or other quadrature methods), floating-point precision can introduce biases or round-off errors. For example:
Very small differences x - y might lead to a small product 6(x - y), which gets lost when added to larger sums, causing underflow or a near-zero contribution.
If the region is highly concentrated in an area with small x - y, you might need a specialized adaptive quadrature that focuses more samples where x - y is small to reduce variance in the estimate.
Numerical stability can also be an issue if sums of positive and negative floating-point numbers occur; in this particular distribution, it’s less of a problem because the pdf is positive in the region. But when dealing with large-scale integrals, standard double precision might be insufficient if we want extremely high accuracy for correlation.
A common pitfall is to rely blindly on numerical estimates without checking convergence or exploring whether the final correlation value is stable over repeated runs and increasing sample sizes.
If we replaced X and Y with transformations (e.g., U = X^2, V = log(Y)), how would we find corr(U, V)?
To find corr(U, V), you need E(U), E(V), E(UV), var(U), and var(V). Specifically:
Express U and V in terms of X and Y: U(X) = X^2, V(Y) = log(Y).
Compute E(U) = E(X^2) by integrating x^2 f(x,y) over the region.
Compute E(V) = E(log(Y)) by integrating log(y) f(x,y) over the region.
Compute E(UV) = E(X^2 * log(Y)) similarly.
Then find var(U) = E(U^2) - [E(U)]^2, var(V) = E(V^2) - [E(V)]^2.
Finally, correlation = [E(UV) - E(U)E(V)] / sqrt(var(U)*var(V)).
Each of these expectations demands new integrals with the joint pdf. A potential pitfall is that log(Y) can go to negative infinity near Y=0, so one must confirm the integral for E(log(Y)) is well-defined and finite over 0 < y < 1. Indeed, log(Y) diverges as Y -> 0, so you must ensure the probability of Y being extremely close to 0 is sufficiently small for the integral to converge. Here, Y can get as small as 0, which might create challenges in the integration if the pdf near y=0 doesn’t sufficiently suppress that region.
How would the correlation change if we artificially clipped the domain at a point less than 1?
Sometimes, in real-world datasets, variables are truncated due to measurement constraints. For instance, if we originally have 0 < y < x < 1 but we decide to only keep data up to x <= c < 1. That effectively changes the region of integration from 0 < y < x < 1 to 0 < y < x < c. Consequently:
The integrals defining E(X), E(Y), and E(XY) would be restricted to 0 < y < x < c.
The pdf might need to be re-normalized to ensure the total probability becomes 1 again over the smaller domain.
This can affect the correlation in unpredictable ways: the truncated domain might emphasize or de-emphasize portions of (x, y) space where X and Y are more or less linearly related.
A pitfall is performing such domain restrictions (data cleaning, outlier removal, or censoring) in real-world analyses without recognizing that it can fundamentally change correlation estimates. You must explicitly re-normalize and re-derive the statistics if the domain is truncated.