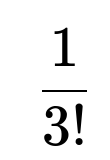ML Interview Q Series: Calculating Ascending Card Sequence Probability via Permutations
Browse all the Probability Interview Questions here.
Suppose you have a deck of 500 cards, each labeled from 1 up to 500, thoroughly mixed. You draw three cards in sequence. What is the probability that each drawn card is strictly greater than the one drawn previously?
Comprehensive Explanation
One way to see the reasoning is to note that whenever you pick 3 distinct cards from a shuffled deck, there are 3! total ways to arrange these three numbers. Only one of these permutations is strictly increasing. Therefore, the probability that you pick three cards in an increasing order is:
Here, 3! is the number of ways to permute 3 distinct items (cards in this case). Because only one of these permutations is strictly increasing, the fraction is 1 divided by 3!, which equals 1/6.
To break it down further:
You first draw any card from the deck. No restriction yet, because there's no previous card to compare with.
For the second card to be larger than the first, and the third card to be larger than the second, it effectively means you are imposing a single strict ordering on the three distinct values you have drawn.
Since the deck is randomly shuffled, every distinct 3-card combination is equally likely to appear in any of its possible 3! permutations. Only one permutation of each 3 distinct cards will be strictly ascending, leading to the probability of 1/6.
Deeper Reasoning and Edge Cases
When dealing with large decks (in this case, 500 cards), each subset of 3 distinct cards can appear in 3! ways with equal probability. The deck size being 500 does not actually affect the probability, since the question focuses on the relative order within those three draws, and each three-card subset is equally likely to appear in any order. Even if the deck had a different number of cards (say 100, 1000, or any n where n >= 3), as long as the cards are distinct and shuffled uniformly, the probability of three draws being strictly increasing remains the same, 1/6.
Example in Python
Below is a brief Python snippet to illustrate a simulation approach (although entirely unnecessary for the final mathematical answer, it helps confirm our understanding):
import random
def simulate_increasing_draws(num_cards=500, trials=10_000_00):
count_increasing = 0
deck = list(range(1, num_cards+1))
for _ in range(trials):
random.shuffle(deck)
draw = deck[:3] # pick the top 3 after shuffle
if draw[0] < draw[1] < draw[2]:
count_increasing += 1
return count_increasing / trials
prob_estimate = simulate_increasing_draws()
print(prob_estimate) # should be close to 1/6
This simulation confirms that the probability approaches 1/6 as the number of trials grows.
Follow-up Questions
Why is the probability the same no matter how many cards are in the deck, as long as we draw only three?
When selecting any 3 distinct cards from a larger set, the internal ordering of those cards is uniformly distributed among all 3! permutations. That means each distinct set of 3 cards is equally likely to be in any order, so only 1 out of 3! orders is strictly increasing, giving 1/6 regardless of the size of the entire deck.
What if we extended the question to drawing 4 cards in sequence? What would be the probability then?
Extending to 4 distinct draws, the probability that they appear in strictly increasing order is 1/4!. In general, if we draw k distinct cards, the probability is 1/k!.
How would the answer change if there were duplicate card values in the deck?
If the deck contains duplicates, then the permutations are not all equally likely to be strictly increasing because some subsets might have repeated values that cannot form a strict ordering. In that scenario, the probability depends on the exact distribution of duplicates. The combinatorial argument of “1 out of k! permutations” only holds for distinct values. For repeated values, one would have to handle the probabilities of drawing certain multisets and the number of strictly increasing permutations of those multisets, which is more complex.
If we needed a non-decreasing sequence instead of a strictly increasing one, how would that change the probability?
For a non-decreasing sequence, each draw can be greater than or equal to the previous. If all cards are distinct, then “greater than or equal to” simply becomes “greater than” because there are no duplicates to make the ‘equal’ part possible. However, if duplicates exist, the probability for a non-decreasing order would be higher. One would need to calculate or simulate the chance that any duplicates appear and contribute to an order that is not strictly ascending but still non-decreasing.
How does this concept generalize for large sequences?
For a sequence of k draws from n distinct, uniformly shuffled elements, the probability of a strictly increasing sequence is 1/k!. This result holds whenever the draws are from a uniformly random permutation of distinct items. The deck size matters only insofar as it must be at least k to avoid repeated values and to ensure distinct draws.
What is the best way to quickly verify this probability in an interview setting?
A quick mental or verbal explanation is to note that for any chosen set of k distinct cards, all k! permutations are equally likely, so the chance of encountering the single sorted arrangement is 1/k!. For k=3, that is 1/6. This logic is easy to convey and typically satisfies interviewers that you grasp the underlying combinatorial principle.
Below are additional follow-up questions
What if the deck is partially ordered or not uniformly shuffled?
If the shuffling process is biased, the assumption that every arrangement of the deck is equally likely is no longer valid. For instance, if some external factor ensures that lower-numbered cards are more likely to appear on top, the probability of drawing cards in strictly ascending order will be higher than 1/6 for a three-card draw. Conversely, if the shuffle tends to cluster larger cards near the bottom, the probability will be lower. To analyze such scenarios, you must quantify or model the bias. Instead of relying on the uniform permutation assumption, you might use probability distributions that describe the likelihood of each card’s position in the deck.
One common approach is to model each card's position as an independent random variable with some distribution that deviates from uniform, then compute the probability of each card i ending up in positions j. However, if dependencies exist between cards, this becomes more complicated. In real-world scenarios like card games with imperfect shuffles, domain knowledge or experimental measurements can help approximate how "random" the shuffle truly is.
How does the probability change if we are drawing with replacement?
When drawing with replacement, after drawing a card, you place it back into the deck, shuffle, and draw the next card. In that scenario, you can draw the same number more than once, which means the event of getting a strictly increasing sequence depends on comparing independently sampled values from a uniform distribution over {1, 2, ..., 500}.
The probability each time you draw is 1/500 for each distinct card value, so for three draws X1, X2, X3 (each in {1,...,500}), you calculate P(X1 < X2 < X3). You can approach this by counting the number of strictly increasing triplets (a, b, c) with 1 <= a < b < c <= 500 and dividing by the total number of possible triplets (500^3). The result turns out to be the same as picking 3 distinct numbers from {1,...,500} in strictly increasing order, because each distinct triple is equally likely. The final probability again is 1/6 that three distinct draws come out in ascending order. The potential difference here is that you might draw duplicates, but those draws automatically fail the strictly increasing condition if a duplicate occurs. Factoring that in still yields the same 1/6 result for the strictly increasing portion among all distinct outcomes, but you must include the draws that repeat values, which further lowers the probability of an ascending sequence.
Specifically, the probability of all three numbers being distinct in draws with replacement is (500/500) * (499/500) * (498/500). Among those distinct draws, 1/6 is in ascending order. If you multiply the fraction of distinct triplets by 1/6, you get the overall chance of a strictly increasing sequence in a draw-with-replacement scenario.
Could this question be extended to ask about the probability of any “peak” or “valley” pattern?
Yes. Instead of focusing on strictly increasing patterns, an interviewer might ask: “What is the probability of drawing three cards that form a peak (first card < second card > third card)?” or a valley (first card > second card < third card)? Analyzing these patterns follows similar combinatorial arguments. Each triplet of distinct cards has 3! permutations, and you can identify how many permutations fit the pattern.
For example, a “peak” pattern among three distinct numbers a, b, c is any ordering where the second is the largest. Among a, b, and c, there are exactly two permutations that produce a peak: a < c < b or c < a < b, provided b is the largest number. Similarly, for a valley pattern, the second card is the smallest. Enumerating these permutations leads to probabilities of 2/6 = 1/3 for a peak pattern (given distinct numbers) or a valley pattern if you define it in a precise manner.
However, if duplicates are allowed, the reasoning changes because for a strict peak, you need the middle card to be strictly greater than both sides, which cannot happen if two or more draws are the same value.
What if we only know the rank order of the cards instead of their absolute values?
Sometimes, you might not care about the actual face values but only the relative ordering. If you only know that a card is, for example, the 10th lowest in the deck, or the 10th after sorting the deck, you can still compute the probability of a strictly ascending pattern. As long as each rank is equally likely and distinct, the probability remains the same: 1/6 for three draws to be in ascending rank order. This highlights that it’s the combinatorial positions that matter rather than absolute numeric labels.
This viewpoint can be extended to any scenario in which you draw 3 items, each with a distinct rank from 1 through N. As soon as you fix the draws, you get a unique triple of ranks, each triple equally likely to appear in any order, so the single ascending permutation has probability 1/6.
Could we estimate confidence intervals around this probability for smaller sample sizes?
If you are running a small-scale experiment, such as physically drawing cards or simulating only a limited number of draws, your estimated probability might deviate from 1/6. If the sample size is small, the proportion of ascending sequences might be noticeably different from 1/6. In such cases, you use statistical techniques (e.g., a binomial proportion confidence interval) to determine how sure you are that the true probability is near 1/6.
For each draw trial, the event “draw is strictly ascending” is like a Bernoulli trial with true probability p = 1/6. Over n trials, the number of successful ascending draws follows a Binomial(n, p). You can compute confidence intervals using standard formulas or methods like the Wilson or Clopper-Pearson intervals.
Does changing the order of draws or indexing them differently affect the probability of ascending order?
If the question were rephrased so that you pick three cards but reveal them in a random order, you might ask: “What’s the probability that the order in which cards are revealed is strictly ascending?” As long as each permutation of the three chosen cards is equally likely, you again get 1/6. The indexing or labeling of the draws does not matter; it only matters that we are comparing three random picks (or the same three picks revealed in random permutations). Each arrangement is equally likely, so the chance one arrangement is strictly ascending is 1 out of the 3! permutations.
What if we draw more than three cards but only check consecutive triplets?
One could ask: if we draw many cards in sequence, how many sets of consecutive triplets are strictly ascending? For a long sequence X1, X2, ..., Xn, there are (n-2) triplets: (X1, X2, X3), (X2, X3, X4), and so on. If n is large and the cards are randomly permuted, the expected number of strictly ascending triplets is (n-2)*(1/6), because each consecutive triplet is equally likely to be in any of the 3! orders (assuming all distinct values). In practice, you can see fluctuations around that mean due to random variation. This observation connects to runs tests and other measures of randomness in sequences.
How might we generalize to the case where we sample an unknown number of cards until a certain event happens?
If the problem is extended to: “We will keep drawing cards one by one until we see three consecutive draws in strictly ascending order,” then we’re dealing with a stopping-time problem. One approach is to treat the state of “how many consecutive ascending draws so far” as part of a Markov chain. The states might be:
0: no consecutive ascending pattern started
1: first card drawn (or we currently have exactly 1 ascending step)
2: two consecutive ascending cards in a row
3: success state (three consecutive ascending draws)
You can then calculate the expected number of draws to reach state 3. However, the transitions depend on comparing the newly drawn card to the previous one, so the exact probabilities need a more nuanced approach because each new draw can either continue the ascending streak or reset it.
In practical card game settings, how do external rules or constraints affect this probability?
Real card games often have special rules like dealing out multiple cards in repeated cycles to different players. In some card games, the deck might be partially seen or known because certain cards have been exposed. All these factors break the assumption of complete randomness or identical distribution for each card. You might need to condition on known cards and recalculate the probability for the next draw. For example, if you already know the highest 50 cards have been removed, the probability distribution over the remaining cards changes. Adjusting for these constraints typically involves conditional probabilities and combinatorial adjustments to the original 1/6 result for three ascending draws.
Without knowledge of which cards were removed or played, you revert to the uniform assumption on whatever remains of the deck. In each step, you update your probability based on the new state of the deck. These real-world complexities make exact calculations more intricate but the fundamental combinatorial principles remain, and you adapt them to partial information and smaller effective deck sizes.