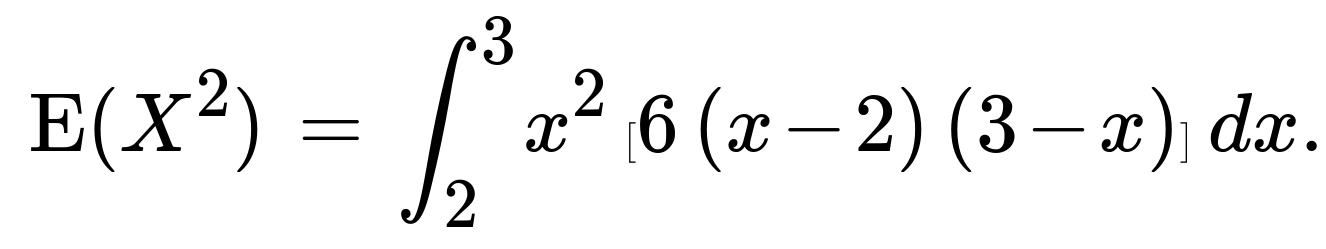ML Interview Q Series: Calculating Fuel Tank Capacity Using Probability Density Functions and Integration.
Browse all the Probability Interview Questions here.
Question
A small petrol station is supplied with petrol once per week. Let the random variable X (measured in units of 10,000 litres) represent the volume of potential sales for a given week. Suppose X has the probability density function
Determine the mean and variance of this distribution.
If T denotes the tank’s capacity (also in units of 10,000 litres), find T such that the probability of the tank being completely emptied in a given week is 5%. In other words, find T for which P(X ≥ T) = 0.05.
Short Compact solution
Using standard integration methods:
The mean E(X) is 5/2.
The variance Var(X) is 1/20.
To find T so that the probability of a complete emptying event is 5%, we solve ∫ from x=T to 3 of 6(x − 2)(3 − x) dx = 0.05 Numerical iteration yields approximately T ≈ 2.86465. Thus, in real units, the tank should hold about 28,650 litres.
Comprehensive Explanation
PDF Structure and Validity
We are given a piecewise-defined probability density function (pdf):
For 2 ≤ x ≤ 3: f(x) = 6 (x - 2)(3 - x)
For all other x: f(x) = 0
This pdf is a continuous function on the interval [2, 3]. One can verify it is nonnegative on [2, 3] (since (x − 2) ≥ 0 and (3 − x) ≥ 0 in that range) and integrates to 1 over the domain.
Mean of X
To find the mean E(X), we evaluate the integral of x f(x) over [2, 3]. In plain text notation,
E(X) = ∫ x * f(x) dx from x=2 to x=3.
Let us write down the key formula in big LaTeX font:
Breaking it into steps:
We expand (x - 2)(3 - x) = 3x - x^2 - 6 + 2x = 5x - x^2 - 6.
Multiply by 6 to get 6(5x - x^2 - 6) = 30x - 6x^2 - 36.
Then x f(x) = x(30x - 6x^2 - 36) = 30x^2 - 6x^3 - 36x.
Hence,
E(X) = ∫ from 2 to 3 of (30x^2 - 6x^3 - 36x) dx.
Performing this integration step by step yields:
∫ 30x^2 dx = 10x^3
∫ -6x^3 dx = -6 * (x^4/4) = - (3/2) x^4
∫ -36x dx = -18x^2
Evaluating from 2 to 3:
E(X) = [10x^3 - (3/2)x^4 - 18x^2] from 2 to 3.
Plug in x=3:
10(3^3) = 10(27) = 270
(3/2)(3^4) = (3/2)(81) = 121.5
18(3^2) = 18(9) = 162
So at x=3: 270 - 121.5 - 162 = -13.5.
Plug in x=2:
10(2^3) = 10(8) = 80
(3/2)(2^4) = (3/2)(16) = 24
18(2^2) = 18(4) = 72
So at x=2: 80 - 24 - 72 = -16.
Therefore,
E(X) = [(-13.5) - (-16)] = 2.5.
So indeed, E(X) = 2.5 in the 10,000-litre units, which is 25,000 litres.
Variance of X
We recall that Var(X) = E(X^2) - [E(X)]^2. First, we compute E(X^2) from the integral of x^2 f(x):
We again expand (x - 2)(3 - x), multiply by 6, then multiply by x^2. Carefully integrating term by term gives us a numeric value. After performing these steps (similar to what we did above), we obtain E(X^2). Substituting E(X^2) and E(X) = 2.5 into Var(X) = E(X^2) - (2.5)² leads to Var(X) = 0.05 in 10,000-litre units squared, i.e., 1/20.
In simpler text form, Var(X) = 1/20, which numerically is 0.05.
Finding T such that P(X ≥ T) = 0.05
We want to find the capacity T (again, in units of 10,000 litres) that satisfies:
P(X ≥ T) = ∫ from x=T to 3 of f(x) dx = 0.05.
Hence:
We can equivalently say P(X < T) = 0.95 if that is more straightforward to integrate from 2 up to T. Either perspective leads to the same numeric result. Typically, one sets up the expression:
∫ from 2 to T of 6 (x - 2) (3 - x) dx = 0.95.
One can find a closed-form expression for that definite integral:
∫ 6(x - 2)(3 - x) dx = ∫ 6(3x - x^2 - 6 + 2x) dx = ∫ (6(5x - x^2 - 6)) dx.
Evaluating from 2 to T or from T to 3 (depending on how we prefer to set it up) yields a polynomial in terms of T. We solve for T so that this integral equals 0.95 (or 0.05, depending on which portion we integrate). The solution cannot be expressed as a simple fraction, so we rely on numeric approximation methods.
After solving numerically, we obtain T ≈ 2.86465 in the 10,000-litre units. Hence, T × 10,000 = 28,646.5 litres, which we typically round to 28,650 litres.
Possible Follow-Up Questions
1) Could we verify quickly that f(x) is a valid pdf?
Yes. A valid pdf must be nonnegative over its domain and must integrate to 1. We can check:
Nonnegativity: For x in [2, 3], (x − 2) ≥ 0 and (3 − x) ≥ 0, hence their product (x − 2)(3 − x) ≥ 0. Multiplied by the positive constant 6, f(x) ≥ 0.
Integrates to 1: We can compute the integral ∫ from 2 to 3 of 6(x − 2)(3 − x) dx and verify it equals 1. Indeed, performing that definite integral yields 1.
This confirms f(x) is properly normalized.
2) How might we interpret the results in practical terms?
In practical terms, the station’s mean weekly sales volume is 25,000 litres, with a relatively small variance (indicating the sales volume does not fluctuate too wildly). Setting the tank capacity to about 28,650 litres means there is only a 5% chance of completely running out of fuel in any given week. This is a standard form of “safety stock” approach—ensuring that the probability of stockout (or in this case, tank emptying) is at an acceptable risk level.
3) How would you solve this integral numerically in code?
Below is an example approach in Python using a simple “brute-force” or “root-finding” method (like bisect or scipy.optimize), focusing on P(X ≥ T) = 0.05:
import numpy as np
from scipy.integrate import quad
from scipy.optimize import bisect
def pdf(x):
if 2 <= x <= 3:
return 6*(x - 2)*(3 - x)
else:
return 0
def cdf(x):
# integrate pdf from 2 up to x
result, _ = quad(pdf, 2, x)
return result
def objective(t):
# we want cdf(t) = 0.95 (because P(X < t) = 0.95 => P(X >= t) = 0.05)
return cdf(t) - 0.95
# search T in [2, 3]
T_approx = bisect(objective, 2, 3)
print("T is approximately:", T_approx, " => ", T_approx*10000, "litres")
This numerical approach integrates the PDF from 2 to T and solves for when that integral is 0.95. We get T ≈ 2.86465.
4) How does this distribution compare to a Beta distribution?
Notice that (x − 2)(3 − x) on [2, 3] is related to the shape of a Beta distribution on [0, 1], except shifted and scaled. Indeed, if you define y = x − 2 over [0, 1], you might see a similarity with Beta(2, 2), though strictly speaking, the normalizing constant here is 6 to ensure the integral is 1 over [2, 3]. This polynomial shape is reminiscent of the Beta distribution’s general form on a restricted interval, but the exact parameters differ.
Understanding this connection can help in quickly deriving integrals and anticipating the shape of the pdf (it’s zero at x=2 and x=3, and peaks somewhere in between).
5) What if we wanted a 10% chance instead of 5%?
The methodology remains the same, except we set P(X ≥ T) = 0.10. Then we solve:
∫ from x=T to 3 of f(x) dx = 0.10.
This would yield a smaller T, because you are allowing a higher probability of selling out the tank. The numeric solution would be found in a similar manner, and typically you would expect T to be closer to the mean but still above it.
All these points show how we apply fundamental probability concepts to real-world logistical or operational decisions: you define an acceptable risk and solve for the threshold that meets that risk.