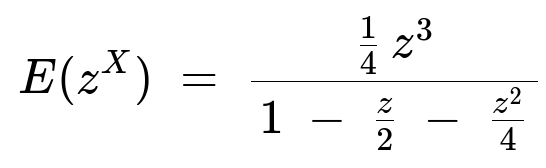ML Interview Q Series: Calculating Stopping Time PGF for Consecutive Bernoulli Trial Runs
Browse all the Probability Interview Questions here.
14E-3. You perform a sequence of independent Bernoulli trials with success probability p. Let the random variable X be the number of trials needed to obtain three successes in a row or three failures in a row. Determine the generating function of X. Hint: let X1 (X2) be the additional number of trials to obtain three successes in a row or three failures in a row when the first trial results in a success (failure).
Short Compact solution
We begin by conditioning on the result of the first trial. If the first trial is a success (which occurs with probability p), then X is 1 + X1. If it is a failure (with probability 1 - p), then X is 1 + X2. Hence:
E(z^X) = p E(z^(1 + X1)) + (1 - p) E(z^(1 + X2)) = p z E(z^(X1)) + (1 - p) z E(z^(X2)).
Next, we characterize X1. The random variable X1 equals 2 if the next two trials are both successes (which happens with probability p^2). Otherwise, after one more trial, we either move into the regime corresponding to X2 or continue similarly. A similar argument applies to X2 (if the initial trial is a failure). Solving the resulting two linear equations in E(z^(X1)) and E(z^(X2)) yields expressions for each of those generating functions. Substituting these back into the expression for E(z^X) then gives the probability generating function of X.
For the special (and simpler) case p = 1/2, we arrive at
This compact form is obtained after considerable algebraic simplification and captures the probability generating function for the number of Bernoulli coin tosses needed to get either three heads in a row or three tails in a row.
Comprehensive Explanation
Overview of the Problem
We have a sequence of independent Bernoulli trials, each trial having a probability p of yielding a “success” (S) and probability 1 - p of yielding a “failure” (F). We stop as soon as we observe either three consecutive successes (SSS) or three consecutive failures (FFF). Our goal is to find the probability generating function (PGF) of X, where X is the total number of trials up to and including the stopping trial.
The PGF of a discrete random variable X taking values in {1, 2, 3, …} is defined as:
E(z^X) = sum_{k >= 1} P(X = k) z^k.
Conditional Approach
Conditioning on the first trial Let the first trial outcome be S with probability p. In that event, we know X = 1 + X1, where X1 denotes the additional number of trials from that point onward until we get three identical outcomes in a row. If the first trial was F with probability 1 - p, we have X = 1 + X2, where X2 is similarly the additional number of trials needed, given that we started with F.
Relation for E(z^X) From the above reasoning,
E(z^X) = p E(z^(1 + X1)) + (1 - p) E(z^(1 + X2)).
Because E(z^(1 + Y)) = z E(z^Y) for any random variable Y,
E(z^X) = p z E(z^(X1)) + (1 - p) z E(z^(X2)).
Equations for E(z^(X1)) We define X1 to be the count of additional trials until we reach either SSS or FFF, knowing that the first trial is S. Now we look at a few more trials:
If the next two trials are both successes (which happens with probability p^2), then we have SSS and stop after exactly 2 additional trials.
Otherwise, we may slip into a situation that effectively looks like “starting with F” or remain in the “starting with S” regime but with partial progress. By carefully enumerating these possibilities (or by focusing on the immediate next trials after the initial S), we get a linear equation in E(z^(X1)) and E(z^(X2)).
Equations for E(z^(X2)) Analogously, X2 is the count of additional trials needed, given the first trial is F. By looking at the next trials:
If the next two are both failures with probability (1 - p)^2, then we have FFF immediately and X2 = 2.
Otherwise, X2 transitions into a scenario that might be effectively “starting with S” or “starting with F” with partial progress, leading again to a second linear equation in E(z^(X1)) and E(z^(X2)).
Solving the Coupled Equations We end up with two linear equations:
E(z^(X1)) = [some expression involving z, p, E(z^(X2))], E(z^(X2)) = [some expression involving z, p, E(z^(X1))].
Solving this system simultaneously for E(z^(X1)) and E(z^(X2)) yields explicit rational functions in z and p.
Substitute Back into E(z^X) Recall E(z^X) = p z E(z^(X1)) + (1 - p) z E(z^(X2)). Plug in the solved forms of E(z^(X1)) and E(z^(X2)). The result is a rather involved rational function in terms of p and z.
Simplification for p = 1/2 When p = 1/2, many terms collapse and the expression simplifies drastically to
This is a neat closed form that can be expanded in a power series to extract probabilities P(X = k) or used to obtain various moments (e.g. E(X), higher moments) by taking derivatives of E(z^X) and then setting z = 1.
Why This Approach Works (Markov Reasoning)
Another (equivalent) way to see this is to define a Markov chain whose states encode the “progress” toward either SSS or FFF. For example:
State 0: No consecutive outcomes yet or just starting.
State S1: Exactly one S in a row so far.
State S2: Exactly two S in a row so far.
State F1: Exactly one F in a row so far.
State F2: Exactly two F in a row so far.
State END: Absorbing state, where we have either three S or three F in a row.
You can write down the transition probabilities between these states and then derive the generating function or distribution of hitting times for the absorbing state. This is mathematically equivalent to the conditioning argument but often clarifies the underlying structure.
Computing E(X) from the Generating Function
One common reason for seeking the probability generating function is to derive the expected stopping time. We know:
E(X) = d/dz [E(z^X)] evaluated at z = 1.
By performing that derivative (and carefully taking the limit as z -> 1), one obtains E(X). In the provided notes, a rather involved algebraic expression emerges for general p, but it is still systematically derivable from:
E(X) = (d/dz) E(z^X) |(z=1).
For p = 1/2, the simplification is more tractable, and one can confirm that E(X) = 7 for the fair coin case.
Potential Follow-Up Questions
How would you explicitly compute P(X = k) for a given k?
To find P(X = k) for each integer k >= 3 (knowing the process cannot stop before 3 trials), expand the generating function E(z^X) = sum_{k >= 1} P(X = k) z^k as a power series in z. In practice, you can do a Taylor series expansion around z = 0. The coefficient of z^k in that expansion is exactly P(X = k).
Can we interpret this problem in terms of a Markov chain hitting time?
Absolutely. As noted above, define states for how many same-outcome-in-a-row have occurred so far. Once we reach either 3 consecutive successes or 3 consecutive failures, the chain transitions to an absorbing state. We are then interested in the distribution of the hitting time to that absorbing state. This is a standard absorbing Markov chain calculation, and from the transition matrix, one can solve for the PGF or for the probabilities P(X = k).
Are there any boundary or edge cases to watch out for?
p = 0 or p = 1. In these degenerate cases, the chain obtains three identical outcomes immediately (strictly speaking, it will be all failures if p = 0, or all successes if p = 1). Then we know X = 3 deterministically. The generating function E(z^X) in that case becomes z^3.
p very close to 0. In this regime, nearly all outcomes are failures, so we expect the distribution of X to be heavily skewed toward small values, because we tend to see FFF quickly.
p very close to 1. Analogously, we see SSS very quickly, so again X is skewed to small values.
How might we simulate this to verify correctness?
You can write a simple simulation in Python:
import random
import statistics
def simulate_sequence(p, n_sims=10_000_00):
results = []
for _ in range(n_sims):
count = 0
consecutive = 0
prev = None
while True:
count += 1
outcome = (random.random() < p) # True for success, False for failure
if outcome == prev:
consecutive += 1
else:
consecutive = 1
prev = outcome
if consecutive == 3:
results.append(count)
break
return statistics.mean(results)
p_val = 0.5
estimated_mean = simulate_sequence(p_val)
print("Estimated E(X) for p=0.5 =", estimated_mean)
Check if the estimated_mean is close to 7 for p=0.5. This provides a straightforward Monte Carlo verification for the expected stopping time.
By confirming the simulation results align with the derived formula (and specifically the mean when p=1/2), we gain confidence that our generating function derivation is correct.
How does this problem generalize to k consecutive successes/failures?
If we want the stopping time for k consecutive successes or k consecutive failures, we can generalize in the same style but would have more states in the Markov chain: S1, S2, …, S(k-1) and similarly F1, F2, …, F(k-1). Then the approach of deriving the PGF or explicit distribution is structurally similar but more algebraically intense as k grows.
All these follow-up considerations underscore how important systematic approaches—Markov chains or well-structured conditioning equations—are for analyzing stopping times in Bernoulli sequences.
Below are additional follow-up questions
Could the process theoretically continue forever, or does it almost surely terminate?
A key insight in these types of Bernoulli processes is that it almost surely terminates. In other words, the probability that we never see three consecutive successes or failures is zero. To see why, note that for an infinite sequence of Bernoulli trials, every finite configuration (such as three identical outcomes in a row) will almost surely eventually appear if there is a non-zero probability of each outcome. Formally, the Borel–Cantelli lemma helps confirm that events with positive probability (in this case, the emergence of three identical outcomes in a row) will occur infinitely often with probability 1. Hence, X is almost surely finite. A subtle pitfall can arise if p=0 or p=1. Then the sequence stops deterministically at trial 3. Otherwise, for any 0<p<1, the process terminates a.s.
How can we compute the probability that the process ends with three successes vs. three failures?
One can define P(end with SSS) and P(end with FFF) by conditioning on the first few trials, similar to how we derived the generating function. If we let A = “the event that the game ends with SSS,” then:
We can form a recursion for P(A) by considering transitions to partial states (e.g. “1 success in a row,” “2 successes in a row,” etc.).
Alternatively, we can sum up P(X=k, and the last three trials were successes) over all k. The direct Markov chain approach is often the clearest: label states by how many consecutive S or F we have, and incorporate transitions leading to the absorbing states SSS or FFF. Then solve for the probability of absorption in the SSS state vs. FFF state. This approach reveals the weighting effect of p on which absorbing state is more likely.
What if the success/failure sequence is not i.i.d. Bernoulli but has dependencies (e.g., a Markov chain with memory)?
The entire derivation of the generating function depends on the independence of each trial and the fixed success probability p. If the trials are correlated—for example, if the probability of success on the next trial depends on past outcomes in a way that is not captured by “consecutive successes/failures” alone—then the simple approach we used breaks down. One would need a more general state-space approach, possibly tracking all relevant history that influences the next trial’s probability. In practical terms, the phenomenon of “runs” in correlated data requires more sophisticated Markov or chain-of-chains methods. A pitfall is to assume that small correlations can be neglected; in some real-world scenarios (e.g., network packet failures), correlations can significantly change the distribution of run lengths.
How would you handle partial fraction decomposition of the generating function to derive a closed-form expression for P(X=k)?
After deriving E(z^X) as a rational function, you can attempt partial fraction decomposition on that function to transform it into a sum of simpler terms whose power-series expansions are straightforward. Once in partial fraction form, each piece can be expanded in a geometric series (or a related expansion), allowing direct reading-off of the coefficient of z^k. A subtlety arises when the denominator factors have repeated roots or complex roots. Handling repeated roots can require polynomial expansions with binomial coefficients. Handling complex roots might mean you must treat conjugate pairs carefully to ensure the final probabilities are real and non-negative.
How would you approach computing higher moments (e.g., E(X^2) or E(X^3))?
To obtain higher moments from the generating function, you can take successive derivatives of E(z^X) at z=1. In text form:
E(X) = d/dz [E(z^X)] at z=1.
E(X(X-1)) = d^2/dz^2 [E(z^X)] at z=1, and so forth. A common pitfall is forgetting to apply the product rule correctly or mishandling the limit as z → 1. The resulting expressions can be fairly involved, so errors can creep in from algebraic manipulation. In practice, symbolic computation tools (e.g., Sympy in Python) can help verify correctness.
How might these results change if we shift the stopping criterion to “two heads in a row or two tails in a row”?
The structure of the derivation remains similar, but you now only need to see two consecutive identical outcomes to stop. That changes the number of states in the Markov chain or the structure of the recursion. The overall approach—conditioning on the first trial and writing separate generating-function equations—is still valid but is simpler because you stop faster. A subtlety is that you can potentially stop in just 2 trials, so the distribution is more heavily weighted toward lower values. The same partial fraction or direct Markov approach can be used to solve it.
What is the relationship between the probability generating function and the moment generating function in this context?
The PGF is E(z^X), whereas the moment generating function (MGF) is E(e^{tX}). Both encode the distribution of X, but the PGF is typically used when X takes values in the nonnegative integers, as it more directly relates to probability expansions. The MGF, being E(e^{tX}), is more commonly used for real-valued random variables in a broader context. For runs and similar discrete processes, PGFs often yield simpler algebra. A common pitfall is to confuse the two and attempt expansions that are more natural under one representation in the domain of the other.
How do numerical stability issues arise when we try to evaluate E(z^X) for z close to 1?
As z → 1, E(z^X) → E(1^X) = 1, but the rate at which it approaches 1 influences the derivatives used for computing moments. If you numerically approximate E(z^X) at values of z near 1, you might encounter cancelation errors if the function and the denominator are both small. This leads to computational instability. One strategy is to use series expansions around z=1 and carefully handle the resulting coefficients. Another is to use higher-precision arithmetic if you directly plug z near 1 into a rational function.
How can the theory of martingales or optional stopping help here?
Sometimes, for certain runs problems, one can attempt to define a martingale with respect to the filtration of coin tosses. Then, by applying an optional stopping theorem, you can glean certain facts about E(X). However, caution is needed because the stopping times in runs problems can be unbounded, and optional stopping theorems typically require integrability or boundedness conditions (or special versions that accommodate unbounded times). A common pitfall is to blindly apply an optional stopping theorem without verifying conditions (e.g., uniform integrability), leading to incorrect conclusions about E(X).
How would we account for a different payoff structure if, for instance, each trial had a different “cost” or “time” associated with it?
If each trial does not contribute a uniform “+1” to the count, the random variable X might no longer simply be the “number of trials.” Instead, we might have a total cost or total time that depends on the sequence of outcomes. This complicates the problem because the stopping condition is still based on consecutive successes/failures, but each step might add a different increment. We would need to consider a more general generating function, perhaps a bivariate generating function capturing both the distribution of the stopping time and the total accumulated cost. Such extensions can appear in real-world contexts where each trial has a variable duration. The standard PGF for “number of trials” must be adapted to handle that more complex structure.