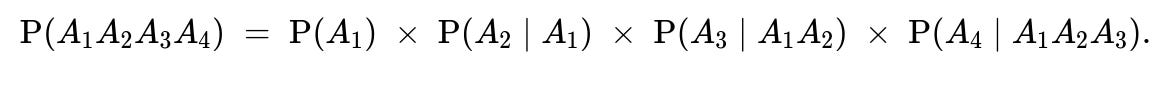ML Interview Q Series: Calculating Sequential Red-Blue Draw Probability with the Chain Rule
Browse all the Probability Interview Questions here.
A bowl contains four red and four blue balls. We draw two balls at a time, four times in total, without replacement. What is the probability that each of the four draws yields exactly one red and one blue ball?
Short Compact solution
We define Aᵢ as the event that the i-th draw (for i = 1, 2, 3, 4) contains one red and one blue ball. By the chain rule for probabilities:
We calculate each term:
P(A₁) = (8×4) / (8×7) = 4/7
P(A₂ | A₁) = (6×3) / (6×5) = 3/5
P(A₃ | A₁ A₂) = (4×2) / (4×3) = 2/3
P(A₄ | A₁ A₂ A₃) = 1
Multiplying these factors gives: 4/7 × 3/5 × 2/3 × 1 = 8/35.
Hence, the probability is 8/35.
Comprehensive Explanation
Understanding the Problem
We have a bowl with 8 total balls: 4 red and 4 blue. We perform four successive draws without replacement; in each draw, we select exactly 2 balls. The question is: what is the probability that every single one of these four draws will contain exactly one red and one blue ball?
To understand why it might be helpful to use conditional probabilities, notice that after each draw, the composition of the bowl changes. Conditioning on what happened in previous draws allows us to break down the calculation step-by-step.
The Chain Rule Approach
A useful tool in probability for sequential events is the chain rule. In plain text, it states that the probability of multiple events happening in sequence is the product of the probability that each event happens given that all the previous events have already happened. Symbolically:
In this problem, Aᵢ = “draw i contains one red and one blue ball.”
Computing P(A₁)
When drawing the first 2 balls from 8 total (4 red, 4 blue), to get 1 red and 1 blue:
Number of ways to choose 1 red out of 4 is 4.
Number of ways to choose 1 blue out of 4 is 4.
Hence there are 4 × 4 = 16 favorable ways to pick 1 red and 1 blue.
The total number of ways to pick any 2 balls out of 8 is 8 choose 2 = 28.
So P(A₁) = 16/28 = 4/7.
Equivalently, we can think of the probability directly:
Probability of picking a red ball first is 4/8, then a blue ball is 4/7 (because one red is gone, leaving 7 total). So that sequence’s probability is (4/8) × (4/7).
Or the probability of picking a blue ball first is 4/8, then a red ball is 4/7. That sequence’s probability is (4/8) × (4/7).
Summing these: 2 × (4/8) × (4/7) = 8/14 = 4/7 (same result).
Computing P(A₂ | A₁)
After A₁ has occurred, the bowl is left with 3 red and 3 blue (because we removed 1 red and 1 blue). Now we have 6 total balls.
So for the second draw, we still want 1 red and 1 blue:
Number of ways to choose 1 red out of 3 is 3.
Number of ways to choose 1 blue out of 3 is 3.
Hence 3 × 3 = 9 favorable ways.
The total number of ways to pick any 2 balls out of 6 is 6 choose 2 = 15.
So P(A₂ | A₁) = 9/15 = 3/5.
Computing P(A₃ | A₁ A₂)
Given A₂ also occurred, that means we have now used up an additional 1 red and 1 blue. So now the bowl should have 2 red and 2 blue left (4 balls in total).
For the third draw, we again want 1 red and 1 blue:
Number of ways to choose 1 red out of 2 is 2.
Number of ways to choose 1 blue out of 2 is 2.
Hence 2 × 2 = 4 favorable ways.
The total number of ways to pick any 2 balls out of 4 is 4 choose 2 = 6.
So P(A₃ | A₁ A₂) = 4/6 = 2/3.
Computing P(A₄ | A₁ A₂ A₃)
If the first three draws were each “one red + one blue,” then across those three draws we have taken away 3 red and 3 blue. Since we started with 4 red and 4 blue, the bowl is left with exactly 1 red and 1 blue (2 balls total). Therefore, the fourth draw cannot be anything other than 1 red and 1 blue. So P(A₄ | A₁ A₂ A₃) = 1.
Final Probability
Multiplying all the conditional probabilities:
4/7 × 3/5 × 2/3 × 1 = 8/35.
So the probability that each draw consists of exactly 1 red and 1 blue ball is 8/35.
Combinatorial Perspective
An alternative way to see this result is through direct combinatorial arguments. If we want exactly 1 red and 1 blue in each of the four draws, then effectively we are partitioning the 4 red balls into the 4 draws (one per draw) and similarly partitioning the 4 blue balls into the 4 draws (one per draw). Then we look at all possible ways to choose 2-ball combinations over 4 draws. Although more involved, this method also leads to 8/35.
The chain-rule approach is often simpler because it naturally uses conditional probabilities that reflect the “without replacement” scenario.
Potential follow-up questions
How would you directly compute this probability using a single combinatorial formula?
One direct combinatorial approach is to consider the total ways of distributing 8 distinct balls into 4 pairs (the order in which the pairs are drawn does matter if each draw is labeled as a distinct event). Then count how many ways assign exactly 1 red and 1 blue to each pair. In detail:
Total ways to form an ordered sequence of four 2-ball draws without replacement: there are 8! permutations of the 8 distinct balls, and then each draw picks the first two, the next two, etc. However, that 8! overcounts because within each pair, the order does not matter, so for each pair we should divide out a factor of 2. Then for the 4 pairs (i.e., 4 draws) in order, the total ways become 8! / (2⁴).
Favorable ways: we want each draw to be 1 red and 1 blue. Label the red balls R1..R4 and the blue balls B1..B4. Assign each of the 4 reds to different draws, and each of the 4 blues to different draws. Once we decide which red ball goes with which blue ball, the order inside a pair does not matter. Then we also consider in which order the draws themselves are chosen. That leads to 4! ways to permute the red balls across the 4 draws, 4! ways to permute the blue balls, then for each pair we have 2 ways to arrange them inside that pair—but again we do not care about the order within the pair. Working through each step carefully will match with the chain-rule result of 8/35.
What if the question asked for a different composition, say 2 red and 0 blue each time?
In that scenario, since each draw is still choosing 2 balls, if the question were about drawing 2 red balls each time for the four draws in total, that would not even be possible because we have only 4 red balls and 4 draws. Two red balls each draw would require 8 red balls total, but we start with only 4. So that probability would be 0. If the question had a feasible scenario (e.g., 2 red, 0 blue for the first two draws and 0 red, 2 blue for the last two draws), you would apply a similar chain-rule approach or a combinatorial approach.
How might this probability change if we sample with replacement?
If after each draw we replaced the balls (returning them to the bowl), each draw would be an independent event. Then the probability that each draw has 1 red and 1 blue would simply be (P(A) for one draw) raised to the power of 4, with P(A) = (4/8)*(4/7)*2 from the usual logic of “choose red first then blue or blue first then red.” But in a with-replacement scenario, each draw is from 8 total balls (4 red and 4 blue) each time, so the calculation changes. Specifically, the probability for a single draw to have 1 red and 1 blue (with replacement factoring in each pick) would be 4/8 * 4/8 * 2 = 1/2 * 1/2 * 2 = 1/2. Then for 4 independent draws, it would be (1/2)⁴ = 1/16.
What practical pitfalls do people encounter with problems like this?
Often, confusion arises when dealing with the difference between “with replacement” and “without replacement.” Another common pitfall is miscounting the ways to form pairs or sets of balls, especially forgetting that the order of draws matters but the order within each draw may not, or vice versa. A thorough approach with conditional probabilities (like we did here) usually avoids many combinatorial mistakes.
How would you simulate this process in Python?
You could do a Monte Carlo simulation by generating many random trials and approximating the probability:
import random
def simulate_draws(num_sim=10_000_000):
import math
success_count = 0
for _ in range(num_sim):
# Balls represented as 'R' or 'B' in a list
bowl = ['R']*4 + ['B']*4
random.shuffle(bowl)
success = True
# We do 4 draws, each of 2 balls
for i in range(4):
draw = bowl[2*i : 2*i + 2]
# check if 1 red, 1 blue
if draw.count('R') != 1 or draw.count('B') != 1:
success = False
break
if success:
success_count += 1
return success_count / num_sim
prob_estimate = simulate_draws(100000)
print(prob_estimate)
As num_sim grows large, the estimated probability should approach 8/35 ≈ 0.22857.
Such a simulation illustrates how to verify theoretical results in practice.
These strategies—conditional probability, combinatorial reasoning, and simulation—are common tools for tackling probability questions in data science and machine learning interviews.
Below are additional follow-up questions
If the problem asked for the probability that exactly 1 red and 1 blue ball occur in each draw, but we do not distinguish the order in which these four draws occur (i.e., the sequence of draws is not labeled), how would the approach change?
When the order of the four draws is not distinguished, we are treating the final outcome as a partition of the 8 balls into four unlabeled pairs. This changes the total ways to form pairs from the 8 balls, because we no longer count different permutations of the same set of pairs as distinct outcomes.
A common pitfall is that people still count each draw sequence as unique and then forget to account for the fact that labeling or ordering the draws inflates the total outcome space. To handle the unlabeled scenario:
Compute the total number of ways to split 8 distinct balls into 4 unlabeled pairs. This is the number of ways to form a set of 4 disjoint pairs from 8 distinct items. It is given by (8!)/(2!2!2!2! 4!) because 8! counts permutations of all balls, dividing by 2! for each pair accounts for the fact that the order within each pair is irrelevant, and dividing by an additional 4! accounts for the fact that the order among the four pairs is also irrelevant.
Compute the favorable ways in which each of the 4 pairs is exactly 1 red and 1 blue. Conceptually, we would place 4 red balls each in different pairs, then 4 blue balls each in different pairs. One subtlety is that once we decide which red goes in which pair, the blue ball for that pair is determined, but the labeling among pairs is irrelevant, so we must be careful not to overcount.
After carefully enumerating both the total and favorable counts in this unlabeled sense, you would again arrive at 8/35. However, the counting steps require more care, and skipping any factor can lead to an incorrect result.
How would the probability change if each draw took place sequentially but you were permitted to reorder the balls between draws in some known or unknown fashion?
If you are permitted to reorder the balls in some fashion between draws (but without actually replacing or removing them), the composition of the bowl does not fundamentally change. You still have the same number of red and blue balls. Hence, from a purely combinatorial standpoint, reordering does not alter the probabilities, because probability depends on the counts of red and blue balls remaining, not on their order.
A subtlety arises in real-world settings if the reordering is not truly random or is influenced by knowledge of prior draws. For example, if someone tries to “cheat” by grouping certain balls together, the draws might no longer be uniform samples from the unchosen balls. Under truly random reordering, the distribution remains the same as if the balls were simply left in place.
A pitfall is to assume that because the balls are “reordered,” you might recast the problem as “with replacement,” which is incorrect. Even if you reorder, no ball is replaced; so the probability should remain unchanged from the standard without-replacement scenario.
What if the question were about the expected number of draws (out of these four) that result in 1 red and 1 blue, rather than the probability that all four draws are 1 red and 1 blue?
The expected value question is a different perspective. You could define Xᵢ as an indicator random variable that equals 1 if draw i has 1 red and 1 blue, and 0 otherwise. Then the total number of desired draws is X = X₁ + X₂ + X₃ + X₄. By linearity of expectation, E[X] = E[X₁] + E[X₂] + E[X₃] + E[X₄].
Each Xᵢ has probability pᵢ = P(Aᵢ). Because the draws are not identically distributed (the composition of balls changes over time), pᵢ may differ for each i. One approach is to calculate these individually by conditioning on the states of the bowl. Another approach is symmetrical arguments—on average, half of the balls are red and half are blue, so you might guess each draw has a certain probability of being 1 red and 1 blue.
A subtlety arises because the draws are dependent: after each draw, the ratio of red to blue in the remaining bowl might shift. Nonetheless, linearity of expectation still applies, even if the variables are dependent.
A typical pitfall here is to assume that the probability for each draw is always 4/7. That is correct only for the first draw. The second draw’s probability is 3/5 only when conditioned on the first event having occurred. One must be careful in computing each expectation term or rely on symmetry arguments if they exist and are valid for each draw.
Suppose we did not draw 2 balls at once but instead drew the 8 balls one by one (without replacement). After every 2 consecutive single-ball draws, we check if they constitute 1 red and 1 blue. Does this change the probability?
Mathematically, it does not. If we say “Draw ball #1 and #2, that forms the first pair. Draw ball #3 and #4, that forms the second pair,” etc., then grouping them into pairs sequentially or literally drawing two balls at once is the same scenario, as long as we treat the final outcome as 4 pairs. The key is that the probability distribution for each pair is the same if we do not reorder or reinsert balls.
An edge case appears if we were to reorder or if the question specifically forbade some outcomes after seeing the first ball. In that manipulated scenario, the probability could shift. But if the 8 draws remain random from the same set of unchosen balls, then partitioning them into consecutive pairs is effectively identical to drawing two balls simultaneously.
A pitfall is incorrectly believing that drawing balls one at a time changes the independence structure. While it changes the story, the underlying combinatorial count remains the same if all draws are uniformly random from the remaining pool.
What if some of the balls are indistinguishable within color? For instance, we cannot tell which red ball is which, but we can still distinguish a red from a blue?
In the original scenario, each ball can be considered distinct (e.g., each might have a small serial number). However, sometimes you might face a scenario where all red balls are truly identical, and all blue balls are truly identical. In such a case, a purely combinatorial approach focusing on the number of red vs. blue outcomes for each draw is simpler: we only care about how many red and how many blue are left after each draw, and not about permutations of identical balls.
This can simplify counting the favorable cases but also can complicate the total number of outcomes if we are used to enumerating permutations. The standard binomial or hypergeometric approach handles this seamlessly, because it only cares about how many red or blue remain, not which distinct red is left. A potential pitfall is to overcount or undercount when switching from “distinct ball” logic to “identical ball” logic. The final numeric answer (8/35) remains the same, since the ratio of favorable to total scenarios is unaffected by labeling as long as we are consistent in counting total ways.
How does this problem generalize to the case of R red balls, B blue balls, and K draws of 2 balls each? Under what conditions is it even possible for each draw to have 1 red and 1 blue?
For each draw to contain exactly 1 red and 1 blue, in total we need K draws that each has 1 red and 1 blue. That implies we must have at least K red balls and at least K blue balls to even make it possible. Then the chain-rule approach generalizes: for the i-th draw, once i−1 draws have occurred, you have R−(i−1) red balls and B−(i−1) blue balls left, out of R+B−2(i−1) total. The probability of 1 red and 1 blue in the i-th draw is:
(R−(i−1)) * (B−(i−1)) / [ (R+B−2(i−1)) * (R+B−2(i−1)−1) / 2 ]
where (R−(i−1)) is the count of red balls left, (B−(i−1)) is the count of blue balls left, and the denominator is the total number of ways to pick any 2 from the remaining R+B−2(i−1) balls. To get the final probability, multiply over i from 1 to K. A major pitfall is forgetting that each draw removes 2 balls (one red, one blue) from each color, so the counts in subsequent draws must be decremented accordingly.
Even more subtle is the condition that it might become impossible at some draw i if R < i or B < i. That means you do not have enough red or blue left for each draw. In that scenario, the probability is 0.
How would you modify the approach if the draws are not all of size 2? For example, you make your first draw of 3 balls, the next draw of 2 balls, the next of 2, and the last of 1 ball. Could that ever yield 1 red and 1 blue “each time”?
That question is trickier because you need to interpret “1 red and 1 blue each time.” If each draw had a size other than 2, “1 red and 1 blue each time” might not even be feasible. For instance, if a single draw is of size 3, you cannot have exactly 1 red and 1 blue in that draw; it would have to be 2 of one color and 1 of the other or 3 of a single color. So the condition “1 red and 1 blue per draw” only makes sense when each draw is exactly 2 balls in size. If the problem states varying draw sizes, you would generalize the condition to “the number of red vs. blue in each draw meets some criterion,” and the chain rule or combinatorial approach would need to be adjusted for each draw size. A pitfall is to blindly apply formulas derived for 2-ball draws to a scenario where draws are of different sizes, leading to an incorrect result.