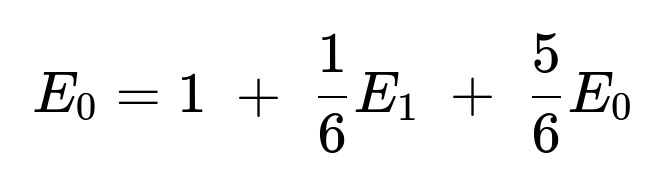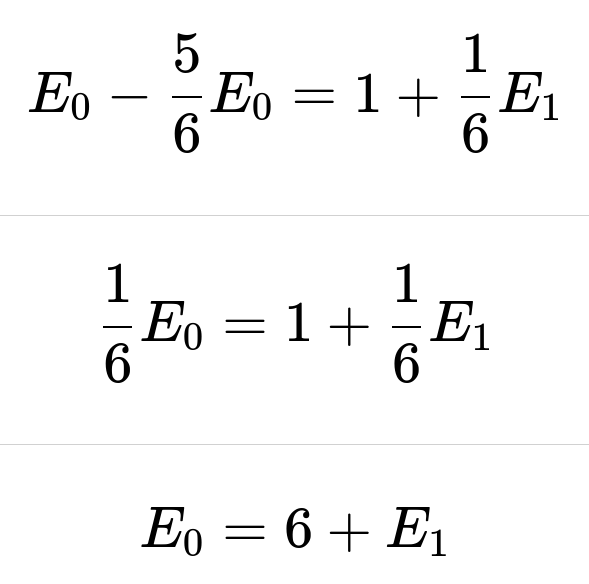ML Interview Q Series: Calculating Expected Rolls for Consecutive 5s Using Markov States.
Browse all the Probability Interview Questions here.
You repeatedly roll a fair six-sided die. How many rolls on average are needed before you see two 5s in a row?
Short Compact solution
Let X be the number of rolls needed to obtain two consecutive 5s. Define Y as the event that the most recent roll was a 5. The idea is to condition on whether the last roll was a 5 or not:
When we have just rolled a 5, we have a 1/6 chance of immediately rolling another 5 (and finishing) or a 5/6 chance of rolling something else, which effectively sends us back to having no consecutive 5 so far.
When we have not just rolled a 5, we roll a 5 with probability 1/6 and move to the “just rolled a 5” state, or we roll one of the other five faces with probability 5/6 and remain in the same state.
Solving the resulting expectation equations gives an expected value of 42 rolls.
Comprehensive Explanation
Defining the States
A powerful way to handle “consecutive success” problems is to break down the process into states representing how close you are to success:
State S0: We have not just rolled a 5, so there is no partial progress toward achieving two consecutive 5s.
State S1: We have just rolled a single 5 on the previous roll, so we need one more 5 to achieve two consecutive 5s.
State S2: We have completed the task (two consecutive 5s) and are done.
Setting up the Equations
We analyze the transitions from one state to another. From S0:
With probability 1/6, we roll a 5 and move to S1.
With probability 5/6, we roll a different number and remain in S0.
Hence, we write:
The “1” in the equation represents the current roll we are using, and then we add the expected rolls needed after we see the result of that roll.
We can rearrange it:
Next, consider S1. From S1:
With probability 1/6, we roll another 5 and finish immediately (contributing 1 roll).
With probability 5/6, we roll something else (not a 5) and revert to S0.
So we have:
The term “0” above is for the case where we succeed right away (once we succeed, there are no more rolls needed). Simplifying:
Solving the System
Now we have a system of two linear equations:
Therefore, the expected number of total rolls to get two consecutive 5s for the first time is 42.
Intuitive Explanation
An intuitive way to see why the number is relatively large:
Rolling a 5 has only a 1/6 chance on any given roll.
Even after rolling one 5, you still have only a 1/6 chance of rolling another 5 right away to complete the pair; otherwise, you have to effectively start over.
This pattern of partial progress, followed by resetting on a failure, means the process can take quite a few rolls on average.
Simulation Approach
We can also verify this result by simulating the process in Python. Although this is not mathematically necessary, simulations are helpful to confirm correctness and build intuition:
import random import statistics def rolls_for_two_consecutive_fives(trials=10_000_00): results = [] for _ in range(trials): count = 0 prev_was_five = False while True: count += 1 roll = random.randint(1, 6) if roll == 5: if prev_was_five: # Achieved two consecutive 5s results.append(count) break prev_was_five = True else: prev_was_five = False return statistics.mean(results) avg_rolls = rolls_for_two_consecutive_fives() print(f"Estimated average rolls to get two consecutive 5s: {avg_rolls}")If you run this simulation for a sufficiently large number of trials, you will see the empirical average hover near 42.
What if the probability of rolling a 5 changes?
If you use a biased die or change the success probability in some other way, the same method applies. You would just replace 1/6 by the new probability p when writing down the transition probabilities, and then solve the resulting linear system. The underlying logic of “states” (no partial success vs. one success so far) remains the same.
How would this extend to three consecutive 5s?
To generalize to three consecutive 5s, you would introduce states that keep track of whether you have 0, 1, or 2 consecutive 5s thus far. You then write down a system of expectation equations similar in style to what we did here, but with one more intermediate state. Solving that system gives the expected number of rolls to achieve three consecutive 5s.
Could this be framed as a Markov chain?
Yes. States S0, S1, and S2 form a Markov chain because the next state depends only on the current state and the outcome of the next roll. Each state transition probability can be placed into a transition matrix, and then techniques from Markov chain theory can be used to solve for the mean time to absorption (with S2 as the absorbing state).
Practical Implementation Considerations
When implementing or simulating in production code, ensure that:
Random seed setting or concurrency issues do not skew results.
Sufficient trials are used in Monte Carlo style simulations to get a stable estimate.
For problems requiring large consecutive runs (like 10 consecutive 5s), direct simulation may be too slow, so a Markov chain approach with closed-form equations is often more efficient and analytically precise.
Below are additional follow-up questions
If the probability distribution of the die outcomes is unknown, how can we still estimate the expected number of rolls to get two consecutive 5s?
One approach is to use an estimation strategy based on observational data. For example, you could roll the (possibly biased) die many times, keep track of the frequency of rolling a 5, and then use this empirical estimate as your probability pp of rolling a 5. From there:
Empirical Probability Estimation: If we do not know the true probability of rolling a 5, we roll the die a large number of times (say N times) and count how many times we see a 5 (call this count cc). Then p≈c/N.
Markov Chain Model: Once p is estimated, the same state-based or Markov chain model can be applied, replacing 1/6 by p in the calculations.
Confidence Intervals: If we rely on the sample-based estimate of p, there is variance around this estimate. We can quantify that variance to produce confidence intervals around the final expected time.
Potential Pitfalls and Edge Cases
Insufficient Samples: If N is too small, the estimate of p may be misleading, especially if the die is heavily biased.
Time-Varying Behavior: If the die’s bias changes over time (e.g., if some environmental factor affects its distribution), then the stationary assumption in the Markov chain model breaks down.
Data Mixing: In real data collection, mistakes in recording rolls or inadvertently mixing data from different dice can skew p.
How do we find the distribution (rather than just the expectation) of the number of rolls needed?
To determine the probability that it takes exactly n rolls to get two consecutive 5s, you can use state-based probabilities over discrete time steps:
Potential Pitfalls and Edge Cases
Large n Computations: The distribution may have a long tail; naive recursion up to a very large n can be computationally expensive if not optimized.
Precision Errors: Repeated floating-point updates to probabilities might accumulate rounding errors, especially if n goes large.
Data Storage: For very large n, storing probability arrays might become memory-intensive if not handled carefully (e.g., storing only partial distributions at each time step).
What changes if the die transitions might “lock” or “stick” on a particular face occasionally?
If there is a mechanism that sometimes forces the die to remain on the same face as a “sticky face” scenario:
Potential Pitfalls and Edge Cases
Non-Markovian: If the “sticky” phenomenon depends on more than just the last roll (for instance, if it sticks only after a certain pattern), the chain might not be truly Markov anymore. Additional states that capture needed history might be necessary.
What if we are only interested in the maximum number of rolls before two consecutive 5s occur, under some constraint?
Sometimes, we might place a cap on how many times we allow ourselves to roll before giving up:
Truncated Processes: We might say “If we haven’t rolled two consecutive 5s by roll M, we stop and declare failure.” In that case, the process is no longer infinite-horizon. We can track the probability of having succeeded by each roll up to M and then conclude with the probability of failure if we still haven’t seen consecutive 5s by roll M.
Expected Value With Truncation: If we want the expected time to success with the condition that if we exceed M rolls, we cut off (and maybe define the time to success as M if not achieved earlier), we can incorporate that into a Markov chain with an additional absorbing state “failed at or after M.”
Potential Pitfalls and Edge Cases
Large M: The difference between the truncated scenario and the infinite scenario might be negligible if M is very large compared to the typical times to get consecutive 5s.
Policy Decisions: If this were a real scenario (e.g., some test procedure that must end by roll M), failing to roll the two 5s before M could have business or operational consequences, so you’d interpret that failure probability carefully.
Non-Standard Definitions: The moment you add a maximum cutoff, the expected value might become less straightforward if success is not guaranteed within M rolls.
How to handle cases where rolling a 5 might invalidate previous rolls under some extra condition (like a “bad 5” scenario)?
Sometimes, problems add twists like: If you roll a 5 when you didn’t want one, you lose progress. Or maybe the second 5 must occur in a certain sequence:
More Complex States: If rolling an unwanted 5 resets the process entirely, you might need more states to keep track of whether you are in a “good 5” or “bad 5” situation. For instance, S0 = “no valid progress,” S1 = “have 1 valid 5,” S2 = success.
State Transition Tweaks: The transition probabilities from S1 might need to check whether the newly rolled 5 meets the correct condition or it is a “bad” 5 that resets you to S0.
Potential Pitfalls and Edge Cases
Ambiguous Condition: The definition of a “bad 5” could be scenario-dependent. If the condition is not entirely memoryless, the chain approach might require an expanded state space capturing more context from previous rolls.
Partial Reset vs. Full Reset: Sometimes, rolling a “bad 5” might only partially reset progress, which complicates the state definitions even further.
Could the approach fail if we incorporate a time-dependent probability for rolling 5 (e.g., the die is wearing out)?
If the probability of rolling a 5 changes with each roll (say it slowly increases or decreases over time):
Non-Stationary Markov Chain: In a standard Markov chain model, transition probabilities do not change with time. If p changes from roll to roll, you no longer have a stationary chain. You would either:
Treat each time step with a different transition matrix, or
Approximate the problem by smaller intervals where p is roughly constant.
How does the answer change if we only accept exactly two consecutive 5s and not three?
That is, the sequence must show exactly two 5s in a row but the next roll (if it occurs) must not be a 5:
New Stopping Condition: We now stop only if we get two 5s in a row followed by a non-5 or if those two 5s occur at the very end. The difference is that if you roll a third 5 immediately after the second one, that might not be considered a valid success (depending on the exact condition).
Expanded States:
S0: No 5 just rolled.
S1: Exactly one 5 just rolled.
S2: Exactly two 5s just rolled (and the next roll was not a 5).
S3: Three or more consecutive 5s rolled (which might invalidate success if the problem states that exactly two are allowed).
Transitions: When you are in S1 and roll a 5, you move to a “temporary success,” but you must confirm the next roll is not 5 to finalize the success state. Alternatively, if it is a 5 again, you move to S3, which might mean you overshot and thus no success.
Potential Pitfalls and Edge Cases
Ambiguous Definitions: Make sure “exactly two consecutive 5s” means we do not count three as having succeeded at two. Some problems might say “at least two consecutive 5s,” so the interpretation changes everything.
Completion Condition: If the problem states that once you get two consecutive 5s, you stop rolling, does that automatically mean the third 5 cannot happen? Or do you continue rolling automatically? The logic must be crystal clear.
What if two consecutive 5s are not equally weighted in cost, or the process has some penalty if it takes too long?
In some real-world applications, we might consider an expected cost that grows with each roll, or different outcomes might have different values:
Discount Factor: Alternatively, we might want a discounted expected cost where future rolls are discounted at a rate γ to account for the time value of money or time preference.
Same Markov Chain, Different Aggregation: We can still use the Markov chain to keep track of how long the process is in each state and compute the cost or discounted sum accordingly.
Potential Pitfalls and Edge Cases
Complex Cost Structures: If the cost structure depends on sequences of outcomes (e.g., a penalty if you hit a 5 when you are in a certain partial success state), you may need an expanded state representation to account for that penalty accumulation.
Infinite-Horizon Summation: If the expected time is quite large and you have a discount factor, you must be certain the sum converges properly and no indefinite state transitions cause partial sums to blow up.
How can this be approached from a generating function perspective?
Potential Pitfalls and Edge Cases
Algebraic Complexity: Solving generating function equations can become quite involved. Mistakes in polynomial expansions or partial fractions can derail the entire derivation.
Radius of Convergence: Ensure that you understand the region in which the generating function converges, though for typical probability generating functions with ∣z∣≤1, things are usually stable.
How would the solution change if we had a dynamic probability that depends on the number of consecutive 5s already rolled?
Imagine a scenario where once you roll one 5, your chance of rolling a second 5 changes. This modifies the process so that:
Does having multiple dice rolling simultaneously change the waiting time distribution for seeing two consecutive 5s on the same die?
If you have multiple dice rolling in parallel each time, but you only care about one particular die hitting two consecutive 5s:
Independence: The presence of other dice might be irrelevant if the problem strictly focuses on a single die’s consecutive outcomes. Each die is an independent process.
Multiple Streams: If you are waiting for any one die among many to show two consecutive 5s, the chance of success in each roll step is higher, and the expected waiting time is shorter. You would model each die’s Markov chain in parallel and look at the minimum time among those K dice to achieve consecutive 5s.
Potential Pitfalls and Edge Cases
Correlation: If the dice somehow interact physically (e.g., collisions that systematically produce correlated outcomes), the independence assumption fails.
State Explosion: If you track all dice simultaneously to find the distribution of the time until the first consecutive 5s among any dice, the state space can grow exponentially if done naively. Careful combinatorial reasoning is needed for an exact solution.