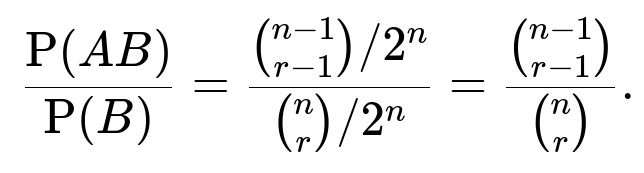ML Interview Q Series: Conditional Probability: First Head Probability Given Total Heads in n Coin Tosses
Browse all the Probability Interview Questions here.
A fair coin is tossed n times. What is the probability of heads on the first toss given that $r$ heads were obtained in the n tosses?
From the structure of the solution, the original question is essentially:
Short Compact solution
To solve this, consider the set of all possible outcomes of n tosses of a fair coin. Each outcome has probability 1 / 2^n. Let A be the event that the first toss is heads, and B be the event that exactly r heads occur in n tosses. The total number of outcomes in B is the binomial coefficient (n choose r), and the number of outcomes in AB (where the first toss is heads and there are r heads in total) is (n-1 choose r-1). Therefore:
P(B) = (n choose r) / 2^n P(AB) = (n-1 choose r-1) / 2^n
Hence the required probability is:
Comprehensive Explanation
A combinatorial view of this problem is the most direct approach. We define:
• n as the total number of coin tosses. • r as the observed total number of heads across all n tosses. • A as the event that the first toss specifically is a head. • B as the event that r heads are observed in total.
Each sequence of length n composed of heads (H) and tails (T) has probability 1 / 2^n. There are 2^n such equally likely sequences.
When we restrict attention to event B, we look only at those sequences that have exactly r heads. The number of such sequences is (n choose r). Therefore the probability of B is (n choose r) / 2^n.
When we consider both A and B together, we require that the first toss is heads, and the total number of heads among all n tosses is r. If the first toss is already heads, then among the remaining n-1 tosses, we must get r-1 additional heads. The number of ways to get r-1 heads out of n-1 tosses is (n-1 choose r-1). Hence the number of favorable outcomes for AB is (n-1 choose r-1), and so:
P(AB) = (n-1 choose r-1) / 2^n.
Dividing P(AB) by P(B):
It is a standard property of binomial coefficients that:
(n-1 choose r-1) / (n choose r) = r / n.
Thus, the required conditional probability that the first toss is heads, given that there are r heads in total, is r / n.
Another intuitive interpretation is the symmetry among all n positions in the sequence. If r heads appear in total, each of the n positions is “equally likely” to be one of those heads, so the probability that the first position is a head is r / n.
Follow-Up Question 1
What if the coin is biased with some probability p of landing heads, rather than being fair?
A more general approach is needed to account for a bias p. Define B as the event that r heads occur among n tosses. Define A as the event that the first toss is heads. By applying Bayes’ rule or directly using a combinatorial argument with probability p for heads and 1-p for tails, one can show:
• P(B) is the probability that r heads occur in n tosses. This is (n choose r) p^r (1-p)^(n-r). • P(AB) is the probability that the first toss is heads and that we have a total of r heads in n tosses. The first toss being heads has probability p, and we need r-1 heads among the remaining n-1 tosses, which has probability (n-1 choose r-1) p^(r-1) (1-p)^(n-r). Combining both factors gives p * (n-1 choose r-1) p^(r-1) (1-p)^(n-r).
Hence,
P(A | B) = P(AB) / P(B) = [p * (n-1 choose r-1) p^(r-1) (1-p)^(n-r)] / [(n choose r) p^r (1-p)^(n-r)].
The p^(r) and (1-p)^(n-r) terms cancel out appropriately, and the ratio of the binomial coefficients is (n-1 choose r-1) / (n choose r). This ultimately simplifies to (r/n), but with p factored in, you will see that the final conditional probability in the biased case becomes r/n when conditioning only on the fact that r heads occurred. If you were asked the unconditional probability that the first toss is heads, that would simply be p. However, once you condition on exactly r heads in total, the dependency among tosses leads back to r/n.
Follow-Up Question 2
How does this result relate to exchangeability in coin tosses?
Exchangeability means that the joint distribution of outcomes does not change if we permute the order of the tosses. For a fair coin, each toss has the same distribution and all sequences of equal numbers of heads and tails are equally likely. When r heads are observed, each of the n positions is equally likely to be among those r heads, leading directly to r/n as the probability that any specific position (such as the first toss) is heads. This is a direct consequence of the fact that the coin tosses are exchangeable: no position in the sequence is more or less favored unless additional information is introduced.
Follow-Up Question 3
If we wanted the probability that the k-th toss was heads, given that r heads were observed, does the same logic apply?
Yes. The argument is essentially identical by symmetry. Whether we look at the first toss or any other k-th toss, the position does not matter for a fair coin. The resulting probability remains r/n, since any toss is equally likely to be among the r heads.
Follow-Up Question 4
What if we have some prior knowledge about the bias p, and then see r heads in n tosses?
This is a Bayesian perspective. Suppose we place a Beta(α, β) prior on p. After observing r heads in n tosses, the posterior for p becomes Beta(α + r, β + n - r). If we are asked about the probability that the first toss (of those n tosses) was heads given that we observed r heads in total, the analysis changes slightly because the event that the first toss was heads can shift how we update the distribution of p. In purely frequentist terms with a known p, the result remains as described in the earlier follow-up question. In Bayesian terms with an unknown p, one typically integrates over the posterior for p to compute conditional probabilities. However, when only the final count r is known (and not the sequence order), by symmetry arguments the position of any single head is still r/n in expectation. This is effectively a consequence of exchangeability across the tosses.
Follow-Up Question 5
Are there alternative ways to see that the conditional probability is r/n without explicitly counting sequences?
One intuitive argument is to imagine the n tosses are symmetrical. If r heads appear, any of the n tosses could be those r heads. There is no reason to prefer one toss over another in a fair coin scenario, so each position among the n tosses must have the same chance of being heads. Therefore out of r heads across n tosses, the fraction of heads in any particular position is r/n. This reasoning can also be made more rigorous through exchangeability arguments or Bayesian updating, but the intuition is often enough in practical scenarios.
Below are additional follow-up questions
Follow-Up Question 1
If r = 0 or r = n, what happens to the conditional probability that the first toss is heads?
When r = 0, this means that out of n tosses, no heads were observed. Consequently, the probability that the first toss was heads, given that there are 0 heads in total, is 0. In other words, if none of the tosses are heads, it’s impossible for the first toss to be heads. Likewise, when r = n, that means all n tosses are heads. In that case, the conditional probability that the first toss is heads is 1, because all tosses (including the first) must be heads.
A potential pitfall in real-world scenarios is forgetting to check boundary cases like r = 0 or r = n when deriving or applying formulas. These extreme conditions often break or short-circuit normal logic. For example, if you used the simplified expression r/n blindly, you get 0/n = 0 for r=0 (which is correct) and n/n = 1 for r=n (which is also correct), so in this specific problem the r/n expression remains valid. However, in more complex probability models (e.g., where p is unknown or when there is correlation across tosses), boundary cases can lead to different behaviors or require slightly adjusted formulas.
Follow-Up Question 2
What if the coin tosses are not independent, such as if there is a correlation between consecutive tosses?
If the tosses are correlated, the classical binomial model is no longer strictly correct. For instance, if the event that the first toss is heads influences subsequent toss outcomes, then we cannot simply count sequences with (n choose r) or (n-1 choose r-1) because the probability distribution for sequences might not factorize into p^r(1-p)^(n-r). The notion of exchangeability might also fail.
To understand the impact on the probability that the first toss is heads given r total heads, one needs a new joint probability model that captures correlations. For example, in a Markov chain scenario, each toss outcome depends on the previous toss with some probability transition matrix. In such a setting, the formula for P(AB)/P(B) can be fundamentally altered, and the r/n result will not necessarily hold. A subtle real-world pitfall could be ignoring these dependencies—perhaps the coin gets slightly stuck more often after landing heads—leading to underestimation or overestimation of the chance of the first toss being a head.
Follow-Up Question 3
How might partial information about the sequence (for example, we know the first two tosses’ outcomes but only the total count of heads for the remaining n-2 tosses) change the result?
In this scenario, the event we condition on is more complex: we know exactly how the first two tosses turned out, and we also know the total number of heads among all n tosses. The question might be: “Given that r heads were obtained in total and that the first two tosses were (H, T), what is the probability that the first toss was heads?” Although it may sound like a strange question (because we seem to already know the first toss was heads from the partial info), this is just an example of how adding partial information about some subset of tosses changes the conditioning.
The general idea is that once partial outcomes are known, the set of possible sequences that match that partial information can shift the distribution in non-intuitive ways. For a fair and independent coin, you can still leverage combinatorial counting: if you already know the result of some subset of tosses, only the remaining unknown tosses factor into the binomial count. However, a key pitfall is mixing up what is known (exact outcomes) versus what is partially known (the total number of heads among the remaining tosses). Each piece of information reshapes the set of feasible sequences, and the naive r/n argument might no longer be correct if the partial information you have specifically references the event of interest (like the outcome of the first toss itself).
Follow-Up Question 4
How do we handle situations where the coin might change its bias mid-way through the n tosses?
Sometimes, the physical characteristics of a coin (or the process generating the heads/tails) can change during the experiment. For instance, imagine that after k tosses, the coin is switched with a different coin having a different bias. If we still record r total heads in n tosses but do not track exactly when the switch occurred, the distribution of outcomes is not described by a single binomial with parameter p. Instead, the total count r arises from a mixture of two binomial processes: one binomial distribution for the first k tosses with parameter p1, and another for the remaining n-k tosses with parameter p2.
To find P(first toss is heads | total r heads in n tosses), you would need a model describing how the coin bias changed and the probability weighting across all possible times the switch could have happened. This can become very involved, as you might need to sum over multiple scenarios that yield the same total number of heads. A pitfall here is to ignore the effect of changing bias and to incorrectly apply r/n logic, leading to a flawed conclusion. Real-world processes often involve unrecognized changes in conditions, so verifying that the coin’s bias remains constant is a critical step.
Follow-Up Question 5
What if the random variable r is not just a single numeric total count of heads but includes extra categories, like a tally of heads, tails, and possibly coin landing on an edge?
In practice, some coins or objects might have a small probability of landing on an edge. If the experiment records “heads,” “tails,” or “edge,” then the sample space and the total outcomes are no longer binary. If we still ask, “What is the probability that the first toss was heads given that exactly r heads were observed?,” we must account for the fact that some tosses might have landed on an edge or in other categories. The combinatorial approach now needs to handle outcomes in a multinomial fashion, rather than a simple binomial.
Specifically, the number of sequences with r heads, s tails, and t edges must be counted accordingly (with s + r + t = n). The total probability of any sequence depends on the probabilities assigned to heads, tails, and edges. The pitfall is incorrectly treating the phenomenon as purely binomial if landing on an edge is non-negligible. In reality, if the coin can land on an edge, r/n might not hold as the straightforward ratio for the first toss, because the conditioning on exactly r heads does not incorporate the distribution of edges properly.
Follow-Up Question 6
How does the result translate if we only have an estimate of r (for instance, we have measurement errors in counting heads)?
In some experimental or practical settings, we might not know r with certainty. For example, if the coin toss outcomes are read by a sensor that sometimes mistakes heads for tails or vice versa, the observed “r heads” might be subject to error. If we define r_obs as the observed number of heads (some of which might actually be tails misread as heads), the probability we want—P(first toss is heads | r heads in reality)—is not necessarily the same as P(first toss is heads | r_obs observed).
To handle this rigorously, you need a model for how r_obs deviates from r. For example, each actual head might be recorded incorrectly with probability ε, and each actual tail might be recorded as a head with probability δ. This leads to a more complicated distribution for r_obs. If you condition purely on r_obs while ignoring misclassification, you risk an incorrect conclusion. Real-world pitfalls include ignoring measurement error altogether or mixing up the distribution of actual heads with the distribution of observed heads, which can produce significant bias in probability estimates.
Follow-Up Question 7
If the experimenter sees the outcome of each toss in real time, does that change the probability that the first toss was heads, given that they ended up with r heads in total?
Observing each toss sequentially in real time does not inherently change the underlying probabilities if the coin is fair and the events remain independent. The conditional probability, after the entire sequence is completed and it’s known that r heads occurred, is still r/n for the first toss. However, the experimenter’s perspective might give rise to psychological or observational biases (“gambler’s fallacy,” for instance) while the experiment is in progress. In theoretical terms, the knowledge gained about intermediate tosses does not change the unconditional or conditional probability regarding the first toss outcome after the experiment is complete.
A pitfall can arise if the experimenter believes that seeing intermediate outcomes can retroactively affect the probability that the first toss was heads. In a purely mathematical model with independence, it cannot. But in reality, if the experimenter can influence the coin toss or if the observation can feed into a changing mechanism (e.g., the experimenter discards certain tosses or stops early), the final count r might not be representative of a straightforward binomial distribution. That would invalidate the neat r/n conclusion.