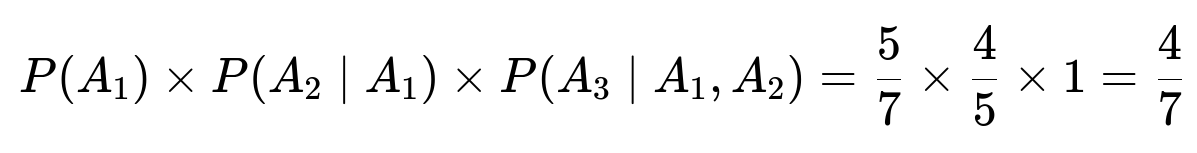ML Interview Q Series: Conditional Probability for Avoiding Clashes in Random Tournament Draws

Browse all the Probability Interview Questions here.

There are three English teams among the eight teams that have reached the quarter-finals of the Champions League soccer. If the teams are paired randomly, what is the probability that the three English teams will avoid each other in the draw?

Short Compact solution

We define A1 as the event that the first English team does not meet another English team, A2 for the second English team avoiding the other English teams, and A3 for the third. By sequentially conditioning these events, the probability is:

Comprehensive Explanation

To understand this probability, note that there are three English teams and five non-English teams, making a total of eight teams in the quarter-finals. When we say the three English teams "avoid each other," we mean that none of the English teams end up playing against each other in the quarter-final matches.

We can interpret the draws as follows:

• There are 8 teams to be paired, resulting in 4 distinct matches.

• The event A1 is that the first English team is not paired with another English team.

• The event A2 is that the second English team also is not paired with an English team, given that A1 occurred.

• The event A3 is that the third English team avoids the remaining two English teams, given that both A1 and A2 occurred.

Below is the step-by-step reasoning to arrive at the probabilities:

When we pick the first English team for a match, there are 7 possible opponents remaining. Out of those 7 teams, 5 are non-English. Therefore, the probability the first English team meets a non-English team is 5/7.

Once that first pairing is fixed (assuming it avoided an English side), we effectively remove those two teams from the pool. We now have 6 teams left. Among them, there remain two English teams and four non-English teams. When it comes time for the second English team to be paired, it must choose from the remaining 5 potential opponents (since one more team gets picked as that second English team’s opponent). Of those 5, 4 are non-English teams. This gives 4/5.

After the second English team also avoids the other English team, we are left with 4 teams total. Within these 4 teams, there remains one English team and three non-English teams. The third English team now inevitably draws from among those 3 remaining non-English sides. Hence, that probability is 1.

Putting it all together multiplies to 4/7. That is the overall probability that all three English teams avoid each other in the quarter-final draw.

Potential Follow-Up Question: Why Multiply the Probabilities?

When events are sequentially dependent (each event affects the probabilities of subsequent events), we use conditional probabilities. The general rule for three events A1, A2, and A3 is:

P(A1 A2 A3) = P(A1) * P(A2 | A1) * P(A3 | A1 A2)

In this scenario:

• A1 is chosen first (the probability the first English team avoids another English team),

• A2 depends on whether A1 happened,

• A3 depends on both A1 and A2 having occurred.

Potential Follow-Up Question: How Might We Generalize This to Four or More English Teams?

If there were four English teams among eight total, the logic would become more involved. You would have to consider the probability each English team draws from the decreasing pool of non-English teams, and these events become more interdependent as more draws occur. The combinatorial approach would also get more complicated, but the reasoning structure remains: compute probabilities of step-by-step avoidance, or systematically count the number of ways to distribute English teams among distinct matches without meeting each other.

In general, an alternative way is to count the total number of ways to pair up the 8 teams and then count the number of valid pairings with no English-vs-English clashes. Dividing the latter by the former yields the same answer. For four English teams, that might be clearer (though more tedious) than a purely stepwise approach.

Potential Follow-Up Question: Can This Be Simulated with a Computer Program?

Yes. One can write a Monte Carlo simulation to approximate the probability. For instance, generate random pairings of the 8 teams many times and record how often the English teams avoid each other.

Here is a brief Python snippet:

import random
import math

def simulate_avoidance(num_simulations=10_000_00):
    english_teams = ['E1','E2','E3']
    other_teams = ['T4','T5','T6','T7','T8']
    success_count = 0

    for _ in range(num_simulations):
        # Create a list of all 8 teams
        teams = english_teams + other_teams
        random.shuffle(teams)

        # Form pairs sequentially
        pairs = [(teams[i], teams[i+1]) for i in range(0, 8, 2)]

        # Check if any pair has two English teams
        clash_found = any(p[0] in english_teams and p[1] in english_teams for p in pairs)

        if not clash_found:
            success_count += 1

    return success_count / num_simulations

prob_estimate = simulate_avoidance()
print("Estimated Probability:", prob_estimate)

This code shuffles the list of all teams, pairs them up in order, and checks if any pair has both members as English teams. By running this simulation many times, one can see that it converges to approximately 4/7 ≈ 0.5714.

Potential Follow-Up Question: What If We Care About the Probability That at Least One All-English Match Occurs?

To find that probability, we can use the complement. Let E = event “no English teams meet.” The probability of at least one all-English match is 1 – P(E). Because we found P(E) = 4/7, it follows that the probability of at least one all-English match is 3/7.

Potential Follow-Up Question: What If We Switch to a Round-Robin or Different Tournament Format?

If the format changed, the probability of English teams meeting one another would depend on the structure (e.g., group stages, round-robin, seeded draws, etc.). The stepwise approach or combinatorial method would still apply, but the details of how many matches are formed and how teams are grouped would drastically alter the probability computation.

Potential Follow-Up Question: Could Seeding Rules Affect This Probability in Real Tournaments?

In many tournaments, teams are not paired strictly at random but are sometimes seeded so that certain teams cannot meet until a particular stage. This drastically changes the sample space for possible draws. In real-world competitions, there may also be rules preventing two teams from the same country from meeting early on. The principle is the same (counting or conditioning on valid draws), but one must incorporate the additional constraints into the probability model.

Potential Follow-Up Question: What Are Some Common Pitfalls When Doing These Probability Calculations?

One pitfall is to overlook the dependence between events. Another is to miscount the total number of ways to pair teams or to assume independence where it does not hold. Also, forgetting that after a team is paired, it is removed from the available pool can cause incorrect denominators. Finally, in more complex draws (especially with seeding or pot assignments), it is easy to double-count or miss valid configurations.

Potential Follow-Up Question: Can We Count Directly Using Combinatorics Instead of Conditionals?

Yes. We can do so by first counting the total number of ways to form pairs among 8 teams. Then we count how many distinct ways result in zero English-vs-English matchups.

For 8 teams, the total number of ways to pair them is given by: (8 - 1)!! = 7 × 5 × 3 × 1 = 105 where n!! (double factorial) is the product of all integers from n down to 1 that have the same parity as n.

Next, to get the number of ways to pair them with no English-vs-English clash, place each of the 3 English teams in distinct pairs with non-English teams. By careful combinatorial arguments or explicit counting, one can also arrive at 60 valid ways, and 60 / 105 = 4/7. This matches the conditional probability approach.

Below are additional follow-up questions

If the order of the matches matters, how does that affect the probability?

In the original problem, we considered only which teams were paired, not the specific order in which they were drawn or which match slot they occupied (e.g., Match 1, Match 2, etc.). If the tournament or the question specifically cares about the order of matches—perhaps the first drawn match is considered more prestigious, or there is some seeding implication—then we have to account for that ordering when we count or list possible outcomes.

• Key Consideration: Once an English team is paired, we not only care about who it faces but also when it was drawn. This modifies the sample space because, instead of just dividing 8 teams into 4 unordered pairs, we would be placing 8 teams into a sequential list that forms matches in a certain order (first two drawn form Match 1, next two drawn form Match 2, etc.).

• Number of Possible Ordered Pairings: If match order matters, one way to think about the sample space is to consider permutations of the 8 teams. There are 8! permutations. However, since pairing the first two teams from the permutation is the first match, the next two teams are the second match, and so on, we must decide how to handle the fact that the order within a pair might not matter (Team A vs Team B is the same as Team B vs Team A). Typically, you would divide by 2^4 to adjust for the fact that each match can be swapped, and still keep the match order the same. Yet if you want strictly ordered matchups (team in slot 1 is home, team in slot 2 is away), you might not even divide by 2^4. The approach depends on the exact question’s interpretation.

• Adaptation of Probability: Once you redefine the sample space to incorporate ordering, you need to recalculate how many permutations (or sequences) result in no English-vs-English clash. If the question remains “What is the probability no English team meets another?” then the result for the probability should remain the same numerically (4/7) if we consistently handle the sample space and event space. The ratio remains the same when properly counting both sets (because the symmetrical ordering expansions apply equally to all possible draws).

• Pitfall: Mixing ordered and unordered counting in the same solution leads to erroneous denominators. You must treat both the favorable outcomes and total outcomes with the same perspective (ordered or unordered).

How does the approach change if we discover partial information about the draw part-way through?

Sometimes we already know the result of one or more pairings before we calculate the probability that the English teams avoid each other. For instance, suppose we know that two non-English teams have already been paired, and now we want to update the probability that no English teams meet given this partial draw.

• Key Idea: This is a conditional probability scenario with updated sample spaces. Instead of having all 8 teams unpaired, we now have 6 unpaired teams left (3 English, 3 non-English, for example).

• Recalculating Probabilities: We would look at the new smaller problem: there are now 6 teams left to draw into 3 matches. We can use a similar approach to the original one—computing P(A1) * P(A2 | A1) * P(A3 | A1, A2)—but with the new pool of unpaired teams. The denominators and numerators change since we have a reduced set of potential matchups.

• Common Mistake: Failing to re-normalize the probabilities after partial knowledge is introduced. Some might keep using the original probability 4/7, forgetting that the situation changed once certain teams have already been drawn together.

What if there is a possibility of a “bye” for a team, meaning not all teams are guaranteed to be paired?

In some tournaments, especially if the number of teams isn’t a power of two, a certain number of teams might get a bye—i.e., they advance automatically without playing. If an English team gets a bye, it does not meet another team in that round at all.

• New Sample Space: Now, instead of forcing all teams into matches, some fraction of teams do not get matched in this round. If 1 or more byes are assigned, we must clarify how they are assigned. Are they chosen randomly among all teams, or are there seeded rules that guarantee certain teams get a bye?

• Effect on Probability: If an English team receives a bye, that automatically satisfies the condition that it does not clash with another English team. Conversely, if byes are assigned randomly, there might be an increased chance that no English teams meet because fewer total pairings happen. However, the method to compute the probability becomes more complex because you must weigh the scenarios under which 0, 1, or more English teams are assigned a bye.

• Pitfall: Assuming no difference between having a bye and being matched. A bye effectively removes that team from the matching process. This changes the composition of teams still needing pairing and so changes the counting or the conditional probabilities.

How do we handle draws if there is a constraint that no two teams from the same country can meet?

Sometimes the Champions League has rules about not allowing teams from the same national association to meet in certain rounds, or it is at least strongly discouraged. If such a constraint is enforced for this stage, the probability is essentially 1 that no English teams meet each other, because it’s disallowed outright. But if there are rules with exceptions—maybe it can happen under certain conditions—then we need to factor that in.

• Adjusting the Sample Space: With a rule “no English vs English,” every possible pairing that violates that rule is removed from the sample space. If that rule is absolute for this round, the result is trivial: the probability is 1 for no clash. If the rule only applies up to a certain point, we have to count how many pairings remain valid and compare it to how many total pairings were initially possible.

• Complication: Real tournaments sometimes have multiple constraints (teams from the same group cannot meet, or certain seeding preferences). This creates a complex set of valid and invalid pairings that require advanced combinatorial logic, often implemented via backtracking or specialized counting techniques.

Could we view this problem from a graph theory perspective?

Yes. Each of the 8 teams is a vertex in a graph. Forming pairs is akin to “perfect matching” in a graph of 8 nodes. We ask: “In how many of these perfect matchings do English vertices fail to connect with each other?” A perfect matching is a set of edges such that every vertex is included exactly once (hence 4 edges connecting the 8 vertices).

• Graph Construction: We label three vertices as English and five as non-English. We want perfect matchings that do not include an edge between any two English vertices.

• Counting Matchings: The total number of perfect matchings in a complete graph of 8 nodes is 7 × 5 × 3 × 1 = 105 (the same (8–1)!! formula we use). The number of perfect matchings that avoid edges between certain vertices can be counted by enumerating only those matchings that skip the edges connecting English-English nodes.

• Pitfall: Graph theory is elegant, but you must be certain to consider all edges that exist or do not exist. If we omit any potential edges (e.g., we consider constraints that some pairings are disallowed for other reasons), then the count of valid perfect matchings changes.

How might real-world broadcast scheduling or logistical constraints alter the random draw assumption?

Broadcast schedules, venue constraints, or policing considerations can influence how UEFA and other leagues arrange draws. For instance, if teams from the same city (even if not from the same country) cannot play home on the same day, or if local police request that certain matches not occur simultaneously, the draw process might not be purely random.

• Impact: If the draw has hidden constraints, the sample space of possible draws is smaller than the theoretical “all pairings are possible.” This might reduce or increase the chance of an English vs English match, depending on how these constraints distribute the matches.

• Real-World Example: If Manchester United and Manchester City cannot both play home on the same day due to policing concerns, the scheduling might forcibly separate them in the draw. In such a scenario, the probability of them meeting each other could go down (or up), depending on the interplay of constraints.

• Pitfall: Overlooking or oversimplifying real-world constraints can cause a mismatch between theoretical probability and actual outcomes seen in practice.

Is there a direct way to adapt the counting argument if, instead of 3 English teams, we had a general number k of English teams among n total?

A direct counting approach typically involves:

1. Counting all ways to pair n teams (which is (n-1)!! for an even n).

2. Counting all ways to form pairs such that k “special” teams avoid each other.

When k grows, the counting approach becomes more complicated. One systematic way is:

• Place the k English teams in matches first, ensuring each is paired with a non-English team if possible.

• Verify that the number of non-English teams is at least k (otherwise it’s impossible to avoid collisions).

• Arrange the remaining teams among themselves.

A general formula can sometimes be expressed in closed form or partial sums, but it typically involves combinatorial arguments that quickly grow in complexity. The logic of step-by-step conditional probabilities still applies but demands more careful tracking of how many English vs non-English teams remain as we form pairings.

Can we verify the result using a symbolic math library instead of a Monte Carlo simulation?

Yes, if one wants an exact symbolic result, libraries like sympy in Python can help enumerate combinatorial possibilities or solve symbolic equations.

• Approach: We can define variables representing the number of English teams E = 3 and the total teams T = 8. Then, we can write expressions for the total number of pairings and for the number of pairings without English clashes. sympy can perform these factorial and combination operations exactly, returning a simplified fraction.

• Advantages: This avoids random noise associated with simulation and avoids manual counting errors. The symbolic result will match the fraction 4/7 precisely for the standard scenario.

• Pitfall: Setting it up incorrectly or failing to define constraints (like no English vs English match) in the symbolic enumeration can still lead to the wrong answer if the logic is not carefully encoded. Symbolic math libraries do not automatically know the logic of your combinatorial problem; you still have to specify it accurately.

What happens if we consider the time order of draws but treat each draw as truly random, pulling teams out of a hat one at a time?

In some real draws, they literally draw Team A out of a pot, then draw its opponent from another pot, and so on. The step-by-step probability approach remains the same in principle, but it can be easier or harder to keep track of how many English vs non-English teams remain.

• Process: Each time you draw a team, you remove it from the pot. Then you draw its opponent. If it’s an English team, you check how many non-English teams remain in the pot. If it’s a non-English team, you proceed similarly. This repeats until all teams are matched.

• Equivalence: Doing a step-by-step hat draw is effectively the same probability as the standard method if done fairly. The sequential steps still yield the same ratio of favorable draws to total possible draws, so the final probability is consistent with 4/7 for no English collisions. The partitioning of the sample space is just being enumerated in a different way.

• Pitfall: Mistakes arise if one miscounts the ways teams can be drawn in sequence or forgets that once an English team is drawn, the number of possible opponents changes for the next step. As always, keep denominators and numerators updated meticulously.