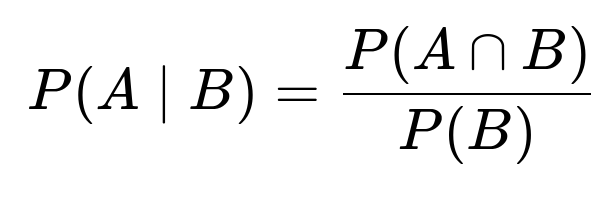ML Interview Q Series: Conditional Probability of Sum 12 from Three Distinct Dice Rolls.
Browse all the Probability Interview Questions here.
29. Say you roll three dice and observe the sum of the three rolls. What is the probability that the sum of the outcomes is 12, given that the three rolls are different?This problem was asked by Facebook.
Understanding The Question
We have three (fair, six-sided) dice. Each die can take one of the values 1 through 6. We want the conditional probability that the sum of the three outcomes is 12, given that all three observed face values are different from each other.
In probability notation, let:
A = “Sum of the three dice is 12”
B = “The three dice all show different face values”
The probability we want is:
We can approach this by counting how many distinct ways (ordered triples) the dice can land to satisfy the events in question.
Detailed Reasoning
Event B: Three Different Faces
Since each die is distinguishable, the number of ways to roll three different numbers on three dice is: 6 choices for the first die × 5 choices for the second die × 4 choices for the third die = 120.
This count (120) represents the total size of event B in the sense of ordered outcomes.
Event A ∩ B: The Sum is 12 AND All Faces are Different
Valid distinct combinations (unordered) of faces that sum to 12:
(1, 5, 6)
(2, 4, 6)
(3, 4, 5)
Why only these three sets?
If we try to build 12 in the range 1 through 6 while ensuring distinctness, these are the only possible distinct sets that sum to 12.
For example, (1, 5, 6) sums to 12 and has all distinct faces. We similarly find (2, 4, 6) and (3, 4, 5). Any other combination either goes out of range (like using 7 or 8) or duplicates a face value.
Next, because we are dealing with ordered triples (the first die, second die, and third die are distinguishable), each unordered set of distinct face values can appear in 3! = 6 permutations. For instance, if the set is (1, 5, 6), we can have (1, 5, 6), (1, 6, 5), (5, 1, 6), (5, 6, 1), (6, 1, 5), (6, 5, 1).
Hence:
(1, 5, 6) yields 6 ordered outcomes.
(2, 4, 6) yields 6 ordered outcomes.
(3, 4, 5) yields 6 ordered outcomes.
Total distinct ordered outcomes summing to 12 = 3 × 6 = 18.
Probability Calculation
We now compute:
Pythonic Approach (Enumerating All Possibilities)
Below is a simple Python code snippet to illustrate the enumeration. This code counts the number of ways to roll three dice that all differ and yield a sum of 12, then divides by the total number of ways to roll three different dice:
count_distinct_sum_12 = 0
count_distinct_total = 0
for x1 in range(1, 7):
for x2 in range(1, 7):
for x3 in range(1, 7):
if x1 != x2 and x2 != x3 and x1 != x3: # all different
count_distinct_total += 1
if x1 + x2 + x3 == 12:
count_distinct_sum_12 += 1
prob = count_distinct_sum_12 / count_distinct_total
print(prob) # Should print 0.15
The output would confirm that the probability is 0.15.
If Dice Were Indistinguishable?
A potential twist is if the dice were considered indistinguishable, in which case we count combinations rather than permutations. That is a different problem entirely, but it often comes up as a follow-up. The logic for that scenario changes the count in both the numerator and the denominator. However, in standard probability questions, we usually treat the dice as distinguishable, meaning each ordering is a distinct outcome.
Follow-Up Question: Could You Derive This Using A Strict Combinatorial Formula Instead Of Enumerating?
Yes. We can directly apply combinatorial logic:
Compute the number of ordered triples summing to 12. Then among those, filter out cases where faces coincide.
Alternatively, use generating functions or the known distribution for the sum of dice. But because we specifically want dice all different, enumeration is typically more straightforward to avoid confusion with repeated combinations.
Follow-Up Question: Are There Any Edge Cases Or Mistakes People Commonly Make In This Problem?
One pitfall is forgetting that the dice are distinguishable. Another pitfall is failing to exclude repeated faces when enumerating or double-counting permutations that have the same combination of numbers but in different orders. Also, some people might mistakenly count the number of ways to get 12 from three dice (25 ways in total with no restriction) and then incorrectly attempt to divide by the total number of ways. This does not solve the question about the conditional probability given the dice are different. The correct approach ensures the condition “all different” is enforced and that we only consider those restricted outcomes.
Follow-Up Question: What If The Question Asked For The Probability Of The Sum Being 12 Without Any Condition?
Without the condition that all three rolls are different, we simply count the total ways to get 12 from three fair dice (ordered). That count is 25. The total sample space is 216. The probability would then be 25/216 ≈ 0.1157. But that is not the question asked here; it’s just a helpful comparison.
Follow-Up Question: What If We Were Asked For The Expected Value Of The Sum, Given That The Three Rolls Are All Different?
We could compute the conditional expected value by enumerating all 120 distinct-outcomes and summing up the sums, then dividing by 120. Alternatively, we could do that programmatically. But that is a more general question than the original one.
All of these follow-up questions highlight how variations in conditions (distinct dice, identical dice, partial constraints) can significantly change the counting, so it is crucial to keep track of constraints carefully and use the correct counting methods.
Hence, the final answer to the original question:
The probability that the sum of the outcomes is 12, given that the three dice are different, is 3/203/20 (which is 0.15 or 15%).
Below are additional follow-up questions
What if each die is biased, and not all faces have equal probability?
How does the approach change if we consider dice with more sides (e.g., 8-sided or 10-sided dice)?
If the dice are not six-sided but n-sided, the logic remains structurally the same, but the counts and sums expand:
Potential pitfalls:
Making assumptions about which sums are possible. For instance, if n<6, the highest face is smaller, and 12 might not be achievable or the distribution might shift drastically.
Forgetting that the new maximum possible sum is 3n, so 12 might be in a different part of the probability distribution. If n=8, 12 is well within range, but if n=5, it might be near the higher end of possible sums.
Handling enumerations for large n becomes more computationally expensive, though for n=8 or n=10, it is still reasonable to brute force. For large n, one might prefer a more analytical approach (e.g., generating functions) while still respecting the distinctness constraint.
How do we handle the probability that the sum is at least 12, given the rolls are different, instead of exactly 12?
The event changes from “sum of the three dice is 12” to “sum of the three dice is at least 12.” Denote:
because there are 120 ordered outcomes that satisfy B (all different).
Real-world subtlety:
“At least 12” lumps together sums of 12, 13, 14, 15, 16, 17, 18. Each sum would have to be enumerated carefully under distinctness constraints.
The difference between “≥ 12” and “> 12” can be a common source of off-by-one errors.
If dice are not fair or not six-sided, the approach remains the same but the details of counting or enumerating shift significantly.
How does the solution change if there is some partial knowledge that one die (say the first die) is a certain value?
If we know in advance that the first die is, for example, 4, then:
Could there be an issue if the dice are physically identical and rolled simultaneously, making permutations effectively the same outcome?
In many real-world probability questions, dice are conceptually distinguishable by time of roll or physical difference. If dice are physically identical and we only observe the multiset of values, the notion of “distinct outcomes” changes:
Under identical dice, the outcome “(1,5,6)” is the same as “(6,1,5)” in the sense that the set of face values is {1,5,6}.
The condition that the three face values must be different is the same, but counting is done by combinations rather than permutations.
The sample space size is smaller since multiple permutations collapse into a single combination outcome if dice are truly indistinguishable.
However, typical textbook probability problems treat dice as distinguishable (different colors or labeled dice). A pitfall:
Mixing up “combinations” vs. “permutations.”
Failing to incorporate or ignoring the factor of permutations that are effectively the same physical outcome if dice are indistinguishable.
In an interview, you would clarify which interpretation is intended.
If we only observe that at most two dice are different, how would it change the problem?
Sometimes, a question might shift the condition to “At most two dice are different.” This implies that either all three dice are the same or exactly two are the same, and one is different. That is a different constraint from “all three dice are different.”
To approach that:
Identify the sub-event of the sample space in which at most two dice are different. This typically breaks into two cases:
All three dice are the same.
Exactly two dice are the same, and one is different.
Within that set, find how many ways the sum is 12. Possibly we’d look for (x,x,x) with 3x=12, or (x,x,y) with 2x+y=12.
Then compute the corresponding conditional probability.
Pitfalls:
Confusion between “at most two different values” and “at most two dice are the same.” They can be stated differently and might cause miscounting.
Overcounting or undercounting the exact scenarios that fall under these constraints.
How might we approach this if we kept rolling sets of three dice and wanted the first time we see a sum of 12 with all three different?
That becomes a geometric or negative-binomial style scenario. If each triple-roll is an independent trial, we can define:
Then the expected number of trials until the first success is either:
If we treat “trial” as any triple-roll:
, where p = Probability(A ∩ B).
If we treat “trial” as only triple-rolls that satisfy B and disregard rolls that have duplicates, that changes the experiment’s structure. We might skip or discard outcomes that do not meet the distinctness criterion, so we only “count” those that are valid. The success probability in that reduced sample is then P(A∣B)=3/20.
Pitfalls:
Misidentifying what counts as a “trial.” If all rolls are considered but we only “check” the ones that are distinct, we have to carefully condition on that scenario or handle the sequence of rolling.
In real dice rolling, we’d observe the dice even if duplicates appear, so ignoring them is conceptually tricky. One might have to incorporate a “Bernoulli trial skipping logic.”
How do we incorporate a real-world scenario where dice might be loaded or damaged over time?
If dice get physically worn down, the probabilities for each face might shift over time. This is a more dynamic scenario:
The probability distribution for each die is not fixed but changes (potentially after each roll).
One might model the changing probability as a Bayesian updating problem or a Markov chain, where after each roll, the distribution might shift.
Pitfalls:
It is easy to ignore the time dynamics if the problem doesn’t specify them, but if an interviewer raises it, they may test your ability to incorporate real-world complexities.
Overcomplicating the model: real dice typically do not drastically change probabilities roll by roll, but in principle, you’d need an estimate of how the distribution evolves to recalculate the sum-of-12 probability at each step.
How can generating functions be used for the distinct-dice sum problem?
A generating function approach typically encodes the ways dice can sum in polynomial expansions. For a single fair six-sided die that can produce outcomes from 1 to 6, the generating function is:
For three dice, if there were no distinctness constraint, the generating function would be:
One approach is inclusion-exclusion, subtracting the scenarios with any repeated faces from the total expansions.
A second approach is to use generating functions for permutations of distinct integers from 1 to 6, though that requires a more intricate polynomial construction.
Pitfalls:
Generating functions can be overkill if the problem only requires a single condition and the dice number is small.
A small error in the inclusion-exclusion step can yield an incorrect count.
Many interviewees might not be fully comfortable with generating function expansions, so enumerations or direct combinatorial arguments may be more straightforward under time constraints.
How do we adapt the solution if we needed the sum to be divisible by 3 given the three dice are all different?
Count how many such triples exist. Divide by 120, the number of distinct-rolled outcomes in total.
Pitfalls:
If one tries to do partial enumeration or shortcuts, it’s easy to miscount.
Overlooking that modular conditions often have uniform distribution properties for random dice, but the distinctness constraint can shift that distribution slightly.
When you compute these probabilities, a brute-force approach in Python is often the simplest, verifying that each triple meets the conditions.
How would the probability change if we define “different” as “no two dice differ by more than 1,” but still want the sum to be 12?
The only triplets that sum to 12 and have each pair of dice differ by at most 1 might be (4,4,4), or (3,4,5) permutations, or (5,4,3), etc. But we’d have to check systematically if those triplets actually differ by at most 1.
For example, (4,4,4) definitely sums to 12, and all dice differ by 0, which is less than or equal to 1, so that’s valid. (3,4,5) also sums to 12, and each pair differs by at most 2. Actually, 5 - 3 = 2, so that does not meet the “differ by at most 1” condition. So (3,4,5) is not valid.
This redefinition of “different” is a nonstandard twist but can appear in tricky interviews to see if a candidate can adapt logic to new constraints.
Pitfalls:
Misreading or misapplying the new distinctness constraint.
Accidentally mixing up “differ by at most 1” with “strictly different.”
Failing to re-verify that (3,4,5) no longer meets the new condition. Many might incorrectly assume it’s valid if they forget the difference constraints.
In any case, the counting or enumeration approach has to be redone from scratch for the new “differences by at most 1” condition.