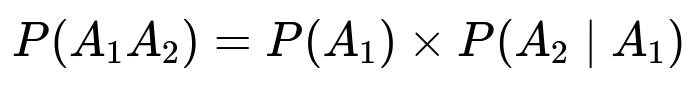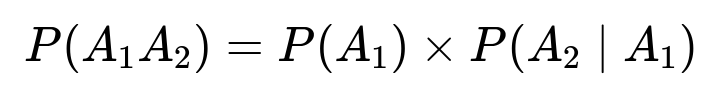ML Interview Q Series: Conditional Probability Applied: Solving Random Distribution and Selection Problems.
Browse all the Probability Interview Questions here.
Questiona) Five people are sitting at a table in a restaurant. Two of them order coffee and the other three order tea. The waiter forgot who ordered what and puts the drinks in a random order for the five persons. Specify an appropriate sample space and determine the probability that each person gets the correct drink.b) Somebody is looking for a top-floor apartment. She hears about two vacant apartments in a building with 7 floors and 8 apartments per floor. What is the probability that there is a vacant apartment on the top floor?c) You and two of your friends are in a group of 10 people. The group is randomly split into two groups of 5 people each. Specify an appropriate sample space and determine the probability that you and your two friends are in the same group.d) You are dealt a hand of four cards from a well-shuffled deck of 52 cards. Specify an appropriate sample space and determine the probability that you receive the four cards J, Q, K, A in any order, with suit irrelevant.Consider again the Problems a), b), c), d). Use conditional probabilities to solve these problems.
Short Compact solution
For part (a), if A1 is the event that the first coffee is given to a person who ordered coffee, and A2 is the event that the second coffee is given to the other person who ordered coffee, then:
P(A1 A2) = P(A1) × P(A2 | A1) = (2/5) × (1/4) = 1/10
For part (b), if A1 is the event that the first vacancy is not on the top floor, and A2 is the event that the second vacancy is not on the top floor, then the probability that there is a vacancy on the top floor is:
1 − P(A1) × P(A2 | A1) = 1 − (48/56) × (47/55) = 0.2675
For part (c), if A1 is the event that your first friend is in the same group as you, and A2 is the event that your second friend is in the same group, the probability that you and your two friends are all in the same group is:
P(A1 A2) = P(A1) × P(A2 | A1) = (4/9) × (3/8) = 1/6
For part (d), if A1, A2, A3, A4 are the events that each of the four cards is the next needed card among {J, Q, K, A}, then:
P(A1 A2 A3 A4) = (16/52) × (12/51) × (8/50) × (4/49) = 9.46 × 10^−4
Comprehensive Explanation
Part (a): Two coffees and three teas distributed among five people
An appropriate sample space can be defined as all permutations of placing two coffees (C) and three teas (T) among five individuals (labeled, for example, Person1, Person2, Person3, Person4, Person5). The total number of ways to distribute two coffees and three teas to five people is the number of combinations of 5 positions chosen for coffee times the arrangement of coffee vs. tea. More concretely, the sample space size is 5 choose 2 for which two people get coffee, i.e. 10 equally likely ways to distribute the two coffees (and the remaining three automatically get tea).
We want the probability that each of the two coffee-drinkers actually receives coffee, and each of the three tea-drinkers receives tea. Imagining the waiter serves the two coffees one by one is a convenient conditional-probability perspective.
Let A1 be the event that the first served coffee is handed correctly to one of the two coffee-orderers. The probability of that event is 2/5, because 2 out of the 5 people actually ordered coffee.
Let A2 be the event that the second served coffee is also handed correctly to the other person who ordered coffee, given that the first one was handed correctly. Once the first coffee has gone to the correct person, there remains 1 coffee-orderer among 4 remaining people, so the probability is 1/4.
The desired probability is:
Substituting the values 2/5 and 1/4 yields 1/10.
Part (b): Probability that there is a vacancy on the top floor
We have a building with 7 floors and 8 apartments per floor, giving a total of 7 × 8 = 56 apartments. Two of them are vacant in random locations among the 56 possible apartments.
Define events: A1 = “The first vacant apartment is not on the top floor” A2 = “The second vacant apartment is not on the top floor, given that the first is not on the top floor”
To calculate the probability that at least one of the two vacant apartments is on the top floor, it can be easier to compute 1 − P(A1 A2), where A1 A2 means “both vacant apartments are not on the top floor.”
There are 8 apartments on the top floor, so there are 56 − 8 = 48 apartments not on the top floor.
P(A1) = 48/56
After the first vacancy is chosen from those 48, there are 47 such apartments left among the remaining 55 apartments total. Thus:
P(A2 | A1) = 47/55
Hence,
= (48/56) × (47/55)
Therefore, the probability that at least one apartment is vacant on the top floor is:
1 − (48/56 × 47/55) ≈ 0.2675
Part (c): Probability that you and your two friends end up in the same group of 5
We have a total of 10 people. They are split randomly into two groups of 5. We want the probability that you and your two friends (call them Friend1 and Friend2) end up in the same group.
Let A1 = “Friend1 is in the same group as me” Let A2 = “Friend2 is in the same group as me, given that Friend1 is also in my group”
The probability that Friend1 is in your group is 4/9. A typical reasoning is that once you are placed, there are 9 remaining slots among the two subgroups, and exactly 4 of those 9 slots are in your particular group of size 5.
Once Friend1 is also in your group, there are now 8 remaining people for 3 spots in your group. So the probability that Friend2 is also in your group is 3/8.
Thus,
= (4/9) × (3/8) = 1/6
Part (d): Probability of receiving J, Q, K, A in any order (suits irrelevant)
You are dealt four cards from a standard deck of 52 cards. We want the probability that those four cards are exactly J, Q, K, A (with any suits and in any order).
Another way to see it is that the first needed card can be any of the 16 possible (4 Jacks + 4 Queens + 4 Kings + 4 Aces = 16 “picture” or “face+Ace” cards we specifically care about). Once the first needed rank is drawn, we look for the second needed rank among the 12 remaining appropriate cards, and so on. We track these events conditionally.
Let A1 = “First card is one of the four ranks we need (J, Q, K, or A), specifically one that we haven’t already drawn.” At the start, there are 16 valid cards out of 52.
Once we have one correct rank, say we got a Jack, we still need the set {Q, K, A} which has 12 cards left in the deck of 51.
Continuing in that way:
= (16/52) × (12/51) × (8/50) × (4/49)
= 9.46 × 10^−4 approximately
This is the probability of getting those four ranks in any suit combination and in any permutation among the four cards drawn.
Possible Follow-up Questions
1) Why do we often prefer to use 1 − P(A1 A2) in part (b) rather than directly counting the probability that there is a top-floor vacancy?
In many probability problems, it is often easier to calculate the probability of the complement of an event (i.e., “there is no top-floor vacancy”) and then subtract from 1. Directly calculating “at least one top-floor vacancy” often involves summing multiple terms (e.g., exactly one on the top floor, or exactly two on the top floor). Calculating the complement typically requires fewer steps and is less error-prone.
2) In part (c), could we also solve for the probability that you and your two friends are together by considering combinations?
Yes. An alternative approach is to directly count the number of ways you and your two friends can be placed together in a 5-person group out of the total ways to form the groups. Specifically, choose 2 additional people (your two friends) out of the remaining 9 to be in your group of 5, which is C(2,2) ways, and then choose the remaining 3 out of the other 7 people for the rest of your group. You then divide by the total number of ways to form two groups of 5 from 10 people. Both methods yield the same result: 1/6.
3) In part (d), what if suits mattered and we wanted the probability of drawing the exact suits as well?
If suits were relevant, then you would need four specific cards (e.g., Jack of Hearts, Queen of Hearts, King of Hearts, Ace of Hearts) in any order. That would change the numerator to 4 “specific” distinct cards and would change the unconditional probabilities at each step. In that case, the probability would be (1/52) × (1/51) × (1/50) × (1/49) if you wanted those four unique cards in any order. The approach still involves conditional probabilities but with 4 fewer desired cards left in the deck each time.
4) How can we generalize part (a) to more people and more drink types?
Suppose we have a total of N people with some distribution of drink orders (for instance, coffee, tea, soda). The probability that each person gets the correct beverage can be computed by a similar chain of conditional probabilities. Specifically, define events that the first correct beverage is delivered to one of the correct recipients, then the second to one of the remaining correct recipients, and so forth, or use permutations and count the number of ways to match people to their correct drinks. The “derangement” perspective or the classical matching approach might also be used for more complicated distributions.
5) Why is conditional probability such a powerful approach for these problems?
Conditional probability allows you to break down more complicated events into a sequence of simpler events that build on each other. It is often simpler to compute P(A2|A1) than to directly count or combine probabilities in a single step. By conditioning on each partial outcome, you keep track of how the sample space “shrinks” (or changes) once an outcome is realized, leading to more direct and intuitive calculations.
Below are additional follow-up questions
1) What if the waiter serves the two coffees to the correct people in part (a), but each of the three teas is randomly placed among the remaining three tea drinkers? Would the probability still be the same?
Answer Explanation In part (a), the probability we computed (1/10) only accounts for whether the correct two individuals receive coffee. That analysis uses conditional probabilities focusing on the coffees alone. However, one might wonder if after correctly placing the two coffees, there is still a chance of incorrectly swapping the teas among the three tea drinkers.
If the question is strictly, “What is the probability that each person gets their exact drink (the correct coffee people get coffee, and the correct tea people get tea)?” then correctly assigning the two coffees automatically guarantees that the other three get tea. Once the 2 coffees have been handed to the right people, the waiter has no choice but to give the remaining 3 cups of tea to the 3 remaining people (all of whom ordered tea).
Therefore, the final arrangement for the tea drinkers does not introduce any further uncertainty for whether someone gets tea vs. coffee. As a result, the probability remains 1/10.
A common pitfall is to mistakenly think we need to multiply by an additional factor for assigning the teas correctly. But once the correct coffee drinkers have been identified, the tea distribution is necessarily correct if we are only distinguishing coffee vs. tea. If instead the teas were distinct (for instance, “jasmine,” “earl grey,” “green tea”), and each tea drinker cared about which exact tea flavor they ordered, the probability analysis would be more involved.
2) In part (b), how would the answer change if there were a total of three vacant apartments instead of two? Would the “1 − P(A1 A2)” trick still be as straightforward?
Answer Explanation When there are three vacancies among the 56 apartments (top floor has 8, other floors total 48), the event “at least one apartment is on the top floor” translates to the complement of “all three vacancies are outside the top floor.” This leads to:
Let A be the event “no vacancy is on the top floor.”
The probability of A is: (48/56) × (47/55) × (46/54), because each vacancy (in sequence) must be chosen from the non-top-floor apartments.
The probability of “at least one top-floor vacancy” is then 1 − [(48/56) × (47/55) × (46/54)].
Yes, the 1 − P(A) approach remains just as straightforward, though we must carefully adjust the numbers to reflect the third vacancy.
A subtlety arises if the question is about “exactly one top-floor vacancy,” “exactly two top-floor vacancies,” or “exactly three.” In those cases, we would break out the binomial expansions or combinations to handle each scenario. But for “at least one” or “at least two,” the complement method continues to be elegant.
A pitfall is to forget that each time we assign a vacant apartment, the total number of remaining apartments decreases and the total number of vacant spots to assign also decreases. Failing to update the denominator and numerator properly can yield incorrect results.
3) In part (c), what if the groups are not of size 5 and 5, but instead one group has 6 and the other has 4 people? How does that affect the probability that you and your two friends are all together?
Answer Explanation The original scenario partitions 10 people into two equal groups of 5. If we change it so that the split is 6 vs. 4, then:
You are in the group of size 6 or in the group of size 4. Suppose we define the event that you end up in the “size 6 group,” but that might not matter if the selection is random and each person is equally likely to be in either group (although typically there are combinatorial ways to choose who goes to the 6-person group).
If you are in the 6-person group, we need both of your friends also to end up in that same 6-person group. Among the remaining 9 people (your two friends plus 7 others), we need to choose which 5 individuals join you to form the group of 6.
One direct approach is:
Probability that you’re assigned to a group that ultimately has 6 people. Often we just say “you’re in the group of 6, end of story,” because any arrangement is symmetrical.
Then the number of ways to pick the other 5 from the remaining 9 is C(9,5).
The number of ways to pick exactly your two friends plus 3 out of the remaining 7 is C(2,2) × C(7,3).
So the probability that your two friends join you in the size-6 group is [C(2,2) × C(7,3)] / C(9,5).
An alternative is the classic “chain of conditional probabilities”:
Probability that Friend1 joins you in your group = 5/9, if we assume the group of 6 is chosen from the remaining 9 to be with you.
Then probability that Friend2 also joins you = 4/8, given that Friend1 is already in your group.
Overall probability = (5/9) × (4/8) = 5/9 × 1/2 = 5/18.
Pitfalls include mixing up the labeled vs. unlabeled group approach, forgetting that the group sizes are different, or incorrectly counting the number of seats left in your group after Friend1 joins.
4) In part (c), what if we want the probability that exactly two of you (out of you and your two friends) are in the same group, rather than all three?
Answer Explanation Sometimes, an interviewer might tweak the question to see if you can handle variations. If “exactly two of us end up in the same group,” it means either:
You and Friend1 are together, but Friend2 is in the other group, or
You and Friend2 are together, but Friend1 is in the other group, or
Friend1 and Friend2 are together, but without you (though that typically doesn’t match the scenario of “you in the same group with one friend”).
There are multiple ways to count or use conditional probabilities. One direct counting approach (assuming two groups of 5 and 5):
First, choose which friend is with you. That is 2 choices (Friend1 or Friend2).
Then for that chosen friend, the probability they are in your 5-person group is 4/9.
Given that friend is with you, the other friend is among the remaining 8 people with 4 spots in your group. So the probability the second friend is not in your group is 4/8 = 1/2.
Hence each scenario has probability (4/9) × (1/2) = 2/9. Because there are 2 symmetrical ways to pick which friend is with you, total is 2 × (2/9) = 4/9. But you must check carefully whether you’re also allowing the possibility that both other friends are together without you, which might change the count.
A frequent pitfall is to double-count scenarios or forget symmetrical cases. Clear enumeration of the sets or using well-labeled events can help avoid confusion.
5) In part (d), how do we handle a scenario where you only care about receiving J, Q, K, A with distinct suits? Would the approach differ?
Answer Explanation If the suits now matter, and you specifically want 4 distinct suits (e.g., J of Clubs, Q of Diamonds, K of Hearts, A of Spades—but any arrangement of those suits as long as each of the 4 ranks is in a different suit), then:
We must count how many ways to pick exactly 1 suit for each of the 4 distinct ranks. There are 4! = 24 ways to assign distinct suits to J, Q, K, A.
For each of those 24 combinations, there is exactly 1 set of four specific cards.
The total number of 4-card hands from 52 is C(52,4).
Therefore, the probability is [24 / C(52,4)].
Alternatively, if you want to do it via conditional probability logic like in the solution snippet, we would have:
P(A1) = 16/52 for drawing any J, Q, K, A (but now we track suit constraints as well).
Then for A2, we must pick a different rank and a different suit from the 12 that remain suitable, or if we specifically want distinct suits, the counting changes.
The direct counting method (24 successful 4-card combinations over C(52,4) total 4-card combinations) is typically simpler. A subtle pitfall is mixing up the logic of “any suit” vs. “specific suits” vs. “4 distinct suits.” Each scenario modifies the numerator in a unique way.
6) What if the deck in part (d) has some cards removed? For example, if we know the deck has only 50 cards total, missing two unknown cards. How would that change the probability calculation?
Answer Explanation When the deck is missing cards but we do not know which cards are missing, the probability that J, Q, K, and A are all present and subsequently dealt to you becomes more complicated:
There is uncertainty over whether the missing cards are among the desired set {J, Q, K, A} or not.
In principle, you would need a conditional probability that the needed cards (J, Q, K, A) are still in the deck. This might involve modeling the missing cards as random draws from the original 52.
A thorough approach might go like this:
Probability that none of the missing cards are among J, Q, K, A. This is (48 choose 2)/(52 choose 2).
If indeed none of the missing cards are J, Q, K, or A, then your probability calculation for getting those 4 ranks out of the 50-card deck is the same style as the original, but with 16 out of 50, then 12 out of 49, etc.
If at least one of the missing cards is among J, Q, K, A, your probability is zero.
You would then combine these probabilities. The pitfall is ignoring the possibility that the missing cards could be crucial to your desired set, thus incorrectly assuming the same odds as a full deck of 52.
7) In part (a), what if each of the 5 people orders a unique drink (e.g., cappuccino, latte, black coffee, green tea, iced tea), and the waiter places them randomly. Can we still use the same approach?
Answer Explanation No, not exactly. The part (a) solution uses the fact that only two distinct types of drinks exist (coffee vs. tea) and lumps them into identical categories (coffee is coffee, tea is tea). If each drink was distinct, the probability that everyone gets exactly what they ordered is akin to computing the probability of a perfect match under a random permutation of 5 distinct objects:
The total number of ways to distribute 5 distinct drinks among 5 people is 5! = 120.
The number of ways to distribute them so that each person gets the correct distinct drink is just 1.
Therefore, the probability is 1/120.
A pitfall is to treat the different types of coffee or tea as if they were still identical. Once distinctness is introduced, we use permutations for each unique item.
8) How do we generalize part (b) if the building has different probabilities of vacancy by floor, i.e., the top floor is more likely to have a vacancy than lower floors?
Answer Explanation If certain floors are more “likely” to have vacancies (perhaps historically top-floor apartments turn over more often), then the vacancies are not uniformly distributed among the 56 apartments. You would need:
A probability distribution over which apartments can be vacant. For instance, let p_i be the probability that apartment i is vacant. The sum of p_i for i=1..56 should match the expected number of vacancies (which is 2 in the original scenario).
The probability that both vacant apartments end up on non-top-floor apartments would be the double-sum (or product if independence is assumed) of the relevant p_i. However, independence might not hold: if one apartment is vacant, it might affect whether a second apartment is vacant.
Real-world complexities:
Apartments might not be vacant independently. You might have constraints like “we know exactly two apartments are vacant, but they’re chosen with some bias.”
Or each apartment’s chance of being vacant could be correlated with others.
A major pitfall is to continue using uniform random selection across all apartments. That would be invalid if the problem states or implies a non-uniform distribution. Modeling that scenario properly can be more complex, often requiring additional data or assumptions to handle correlations.
9) In part (c), suppose we randomly assign people to the two groups by listing all permutations of the 10 individuals and then splitting the first 5 into Group A and the next 5 into Group B. Are we effectively overcounting?
Answer Explanation If we list all permutations of 10 individuals, there are 10! permutations. Splitting the first 5 in the permutation into Group A and the last 5 into Group B will indeed generate each distinct division multiple times because permuting people within the same group does not produce a genuinely different group composition.
To get the number of distinct ways to form (5,5) groups from 10 people, we can do:
Number of ways to choose 5 out of 10 to form Group A is C(10,5). The remaining 5 automatically form Group B.
Each group composition is counted 5! × 5! times if we consider permutations within Group A and Group B. Another factor 2! arises if the groups are unlabeled and we do not care which group is A or B.
Hence, if we want to use permutations to reason about probabilities, we must account for these duplications. A typical pitfall is to equate permutations with equally likely group splits without dividing out the overcounts. The standard, simpler approach is just to note that the total ways to choose a 5-person group from 10 people is C(10,5), which avoids the overcount.
10) In part (d), how do we extend the logic of sequential conditional probability if we wanted 5 specific ranks (e.g., 10, J, Q, K, A) in a 5-card hand?
Answer Explanation You can follow the same pattern but with 5 steps:
Probability that the first card is among the 5 ranks you need. Initially, there are 20 cards of interest (4 per each of the ranks 10, J, Q, K, A) out of 52 total.
Probability that the second card is one of the remaining 16 needed cards out of 51.
The third is 12 out of 50, the fourth 8 out of 49, and the fifth 4 out of 48.
Thus the sequential approach would give:
(20/52) × (16/51) × (12/50) × (8/49) × (4/48)
You can also verify using combinatorial counting: the number of ways to pick exactly {10, J, Q, K, A} in any suits from 52 is 4^5 = 1024 ways (since each rank can come from 4 suits). Total 5-card hands is C(52,5). The direct ratio 1024 / C(52,5) should match the product of fractions above, ensuring consistency.
A subtle pitfall is to confuse the order in which the cards appear with the final 5-card combination. If you do the sequential method, you typically incorporate ordering. However, each of those sequential events is still valid because you account for the correct fraction at each step. The final probability is the same as if you used a combination-based argument.
11) Could we solve part (a) by directly counting favorable arrangements versus total arrangements, instead of using conditional probability?
Answer Explanation Yes. The total number of ways to assign two coffees (C) and three teas (T) to five people is C(5,2) = 10. Exactly one of those ways corresponds to the correct assignment for the two coffee drinkers. Hence the probability is 1/10.
Alternatively, if you prefer enumerating permutations in which each seat or person is labeled:
There are 5 labeled seats (Person1, Person2, Person3, Person4, Person5).
The number of ways to place 2 coffees and 3 teas distinctly is 5! / (2!3!) if the coffees are identical to each other and the teas are identical to each other. However, that formula is actually the multinomial coefficient for rearranging items in a sequence; if each seat is distinct but coffee cups are not labeled among themselves, it reduces to C(5,2).
The one favorable arrangement is the unique distribution matching the 2 coffee orders exactly.
A pitfall is overcomplicating the counting method (e.g., using 5! incorrectly if you think each cup is distinct). The simplest is indeed “choose 2 of the 5 people to get coffee.”
12) What is the biggest misconception students often have with part (d) when dealing the four cards?
Answer Explanation A common misconception is to think we should first choose any 4 ranks out of 13, then multiply by something else to handle suits. Or they might do a combination approach incorrectly by mixing up the difference between “exactly those ranks” and “any suits,” or confuse order with combination.
One classic mistake: “We want J, Q, K, A, so that’s 1 way to choose the ranks out of 13. Then for suits, we pick 4 suits out of 4 possible for each rank, so 4 × 4 × 4 × 4 = 4^4. Then we do that over C(52,4).” That part is actually correct for any suit.
However, if they then multiply by an extra factor or do something else for permutations, they might incorrectly double count.
Another pitfall is ignoring that the deck draws are sequential without replacement. The correct method either uses the product rule with conditional probabilities or uses direct combinatorial counting. Both methods yield the same numerical result.
13) In part (b), suppose we discover that the two vacant apartments are known to be on different floors (no two vacant apartments can be on the same floor). How would that change the probability calculation for a top-floor vacancy?
Answer Explanation Now we have the additional constraint that the two vacant apartments must be on two distinct floors. If the building has 7 floors, each with 8 apartments:
We first pick which 2 floors out of the 7 have vacancies: C(7,2) ways.
Then for each chosen floor, we pick 1 of the 8 apartments: 8 × 8 = 64 ways for each pair of floors.
Total number of ways to place the vacancies is C(7,2) × 64 = 21 × 64 = 1344.
If we want the probability that at least one is on the top floor:
Number of ways in which the top floor is chosen is: Pick the top floor plus 1 of the remaining 6 floors: C(6,1) = 6 ways to pick that second floor. Then pick 1 apartment out of 8 from the top floor and 1 out of 8 from the chosen other floor: 8 × 8 = 64. So total ways is 6 × 64 = 384.
Hence the probability = 384 / 1344. You could simplify that fraction or approximate it numerically.
A big pitfall is failing to account for the “different floors” constraint. If you used the old method (48 out of 56, etc.), you would be implicitly allowing both vacancies on the same floor, which is no longer possible by assumption.
14) If in part (c) we consider the scenario that the two groups are labeled “Team A” and “Team B,” does that labeling change the probability that you and your friends are in the same group?
Answer Explanation It does not change the probability. Whether or not we label the groups, the chance that all three of you end up together is unaffected because the grouping is random. Labeling the groups generally matters if we track which specific group you’re in or if we treat switching groups as producing a “new outcome.” But for the event “all three are in the same group,” the labeling does not alter the underlying probability.
A possible pitfall: Overcounting or undercounting the total number of ways to form the groups once you impose labels. A well-rehearsed approach is that the total ways to put 10 people into two labeled groups of 5 is C(10,5). But the final ratio for the event that you and your two friends are in the same group remains 1/6.
15) In part (d), can we use hypergeometric distributions? How does that perspective work?
Answer Explanation Yes, the hypergeometric distribution is often used when drawing without replacement from a finite population with a certain number of “success” items. For part (d):
The deck has 52 cards total, with 16 “target cards” (4 each of J, Q, K, A).
We draw 4 cards. We want “all 4 draws are from these 16 target cards,” which would mean we get one of each rank if we’re specifically focusing on rank only.
But if we only want the distribution among 16 “special” ranks, we also need to ensure each rank (J, Q, K, A) is represented exactly once, which is a more specific partition than the standard hypergeometric approach of “4 draws from 16 special cards.” Usually, hypergeometric deals with “how many special items are in my sample?” not “did I get exactly 4 distinct ranks?” So you’d refine that to break it down rank by rank.
A simpler method is direct combinatorial arguments or the sequential conditional probability. However, the hypergeometric viewpoint is still valid if you reframe the question as: “What is the probability that the number of Jacks, Queens, Kings, and Aces in the 4 drawn cards is exactly 1 in each category?” which is a multinomial hypergeometric perspective.
One pitfall is to misapply the simpler hypergeometric formula for “k successes in n draws” if we do not adapt it to capturing the distribution across multiple categories (J, Q, K, A). The standard hypergeometric distribution covers a single category at a time, not multiple categories simultaneously.
16) If in part (a) we want the probability that exactly one of the coffee drinkers gets coffee, how would we calculate it?
Answer Explanation This event means exactly one person who ordered coffee does get coffee, while the other coffee goes to a tea drinker. We can approach it through:
Number of ways to choose which coffee drinker receives coffee: 2 ways (either coffee-drinker1 or coffee-drinker2).
That coffee is assigned correctly (probability 2/5 if done step by step).
The second coffee is assigned incorrectly (i.e., to a tea drinker), which, if done sequentially, is 3/4 after the first correct assignment.
Hence a sequential viewpoint: (2/5)*(3/4) = 6/20 = 3/10. But we must be careful: that method might double-count if we do not keep track precisely. Actually, it’s simpler to do direct combinatorial logic:
Exactly one of the 2 coffee drinkers gets coffee: among the 2 coffee cups, 1 goes to the correct coffee drinker and 1 to a tea drinker.
The total ways to distribute 2 coffees among 5 people is C(5,2)=10.
The number of ways to choose exactly 1 correct coffee drinker from the 2, and 1 from the 3 tea drinkers, is C(2,1) × C(3,1) = 2 × 3 = 6.
Probability = 6/10 = 3/5.
Notice that’s 3/5, not 3/10. The difference arises because in the sequential method, you’d have to consider each coffee cup individually. If you do it carefully:
Probability that the first coffee goes to a coffee drinker is 2/5, and the second coffee goes to a tea drinker is 3/4. That product is 6/20 = 3/10.
But the opposite sequence (first coffee goes incorrectly to a tea drinker, second coffee goes correctly to the remaining coffee drinker) has probability (3/5)*(2/4) = 6/20 = 3/10.
Add them up: 3/10 + 3/10 = 6/10 = 3/5.
A common pitfall is to forget to add both possible sequences (correct-then-incorrect or incorrect-then-correct), thereby ending up with half the correct probability.
17) In part (b), if the occupant specifically wants the top-floor apartment only if it faces a particular direction (say each floor has 4 apartments facing East and 4 facing West), how does that refine the problem?
Answer Explanation If you only consider a top-floor apartment acceptable if it is facing East (and presumably there are 4 East-facing apartments on the top floor), then effectively you only have 4 “desired” apartments out of the total 56. To find the probability of “at least one vacancy that is top-floor, East-facing,” you can do:
Complement approach: Probability that none of the 2 vacant apartments is among those 4 East-facing top-floor apartments. This is (52/56) × (51/55) if we assume two random vacancies.
Then subtract from 1 to get the probability that at least one such apartment is vacant.
A subtlety is that it is now a smaller subset of the top floor, so you might want to check if you also accept a West-facing top-floor apartment. If not, only those 4 East-facing apartments matter.
Pitfalls include mixing up the event “at least one top-floor vacancy” with the narrower event “at least one East-facing top-floor vacancy.” Also, some might incorrectly count 8 top-floor apartments total but forget to limit to the East-facing subset if that is the occupant’s requirement.
18) For part (c), how do we handle the scenario that not all group splits of 10 people are equally likely? For instance, what if certain individuals are more likely to be grouped together?
Answer Explanation Realistically, group assignments might not be uniform. Maybe there’s a rule or preference that tries to keep certain pairs of people together. Then the probability distribution over all possible (5,5) splits is no longer uniform.
To handle that, you need to specify or estimate the probabilities of each distinct group composition. For instance, if persons A and B are more likely to end up together, that means the arrangement “A and B in the same group” has a higher probability mass than random uniform selection.
In that more complex scenario, you either
directly sum the probabilities of all group compositions that keep you and your two friends together, or
adopt a suitable model (like a Markov chain approach, or a constraint satisfaction approach).
A pitfall is to assume uniform random grouping when the question states or implies some dependency or bias. You need the exact distribution for correctness. In practice, incomplete or ambiguous information about how groups form can lead to guesswork.
19) In part (d), what if we were only interested in the probability of drawing any 4 consecutive ranks (e.g., 2,3,4,5 or 10,J,Q,K) rather than specifically J, Q, K, A?
Answer Explanation We can generalize:
The sets of 4 consecutive ranks in a standard deck are: (A,2,3,4) if you treat Ace as low, or (J, Q, K, A), or everything in between. Typically, if Ace only counts as high, then the consecutive sequences are (A,K,Q,J) in reverse, but the standard approach typically identifies: (A,2,3,4), (2,3,4,5), (3,4,5,6), up to (10,J,Q,K), (J,Q,K,A). That yields 10 possible rank-sequences if Ace is counted high, or if we allow Ace as low, we might have 10 or 11 sequences depending on conventions.
For each consecutive rank set, there are 4 cards per rank, so 4^4 ways to pick suits for that sequence.
So if there are 10 distinct rank windows of length 4, each window has 4^4 possible 4-card combos.
Probability = (10 × 4^4) / C(52,4), assuming all 4 consecutive ranks are equally likely and that we are ignoring order.
Pitfalls:
Overlooking whether Ace can be both high and low.
Double-counting if we’re not careful about whether a set like (Q,K,A,2) is valid.
Mixing up the question of “in any order” vs. “in sorted rank order.” If the question states “in any order,” that’s already accounted for in the combination count of 4^4 suits. If it wanted them specifically in ascending order in the dealt hand, that’s a different probability.
20) For part (a), does the probability 1/10 change if the waiter distributes all five drinks simultaneously (e.g., placing them in front of each person all at once) vs. distributing them sequentially?
Answer Explanation No, it does not change. Whether the waiter places the cups simultaneously or one by one (with or without noticing mistakes in between) does not affect the overall probability that exactly the two coffee-drinkers receive coffee. The final arrangement in either scenario is equally likely among all possible permutations.
The sequential approach using conditional probabilities is just one convenient way to arrive at the same result. If we define a uniform random distribution of drinks to people, all that matters is that among the 5 persons, exactly 2 of them (the correct 2) get coffee. The resulting probability is 1/10.
A pitfall is thinking that sequential vs. simultaneous distribution might create different probabilities. As long as each final arrangement is equally likely, the probability remains the same.