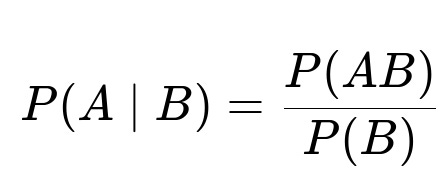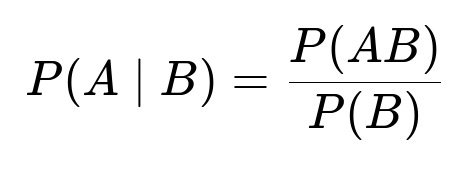ML Interview Q Series: Conditional Probability: Calculating Dice Sum=10 Given Distinct Rolls.
Browse all the Probability Interview Questions here.
Three fair dice are rolled. What is the probability that the sum of the three outcomes is 10 given that the three dice show different outcomes?
Short Compact solution
To find the probability that the sum is 10 (event A) given that all three dice show different results (event B), we use the formula
The event AB (“sum is 10 and all dice are different”) includes exactly the 3! permutations of {1,3,6}, the 3! permutations of {1,4,5}, and the 3! permutations of {2,3,5}. Each set contributes 3! = 6 distinct outcomes, and since there are 3 such sets, that gives 18 total outcomes. Because each of the 216 possible ordered triples is equally likely:
P(AB) = 18/216 = 1/12
The probability that all three dice show different results is (6 × 5 × 4)/216 = 120/216 = 5/9. Hence,
P(A|B) = (1/12) / (5/9) = 3/20
Comprehensive Explanation
Understanding the Events
Let i1, i2, i3 be the outcomes of rolling three fair dice. Each of i1, i2, i3 can independently take values in {1, 2, 3, 4, 5, 6}, so there are 6 × 6 × 6 = 216 total ordered outcomes.
Event A: The sum of the three dice is 10. In plain text form: i1 + i2 + i3 = 10.
Event B: All three dice show different values; i1, i2, i3 are pairwise distinct.
Counting P(AB)
We want the event that the dice are all distinct and that their sum is 10. First, we look at which distinct triples (unordered) sum to 10:
1 + 3 + 6 = 10
1 + 4 + 5 = 10
2 + 3 + 5 = 10
Each distinct triple can appear in 3! = 6 permutations when considered as an ordered triple (for example, (1,3,6), (3,1,6), (6,1,3), etc.). So for each of the three distinct sets, we have 6 permutations. That yields 3 × 6 = 18 total ordered outcomes that meet both conditions (sum to 10 and all dice are different). Because each outcome in the sample space has probability 1/216, we get:
P(AB) = 18/216 = 1/12
Counting P(B)
The probability that all three dice show different values comes from counting how many ways we can pick three different faces out of six and then arrange them. Concretely:
For the first die, we have 6 possible outcomes.
For the second die, we have 5 possible outcomes (anything but the first).
For the third die, we have 4 possible outcomes (anything but the first two).
So the total number of favorable outcomes is 6 × 5 × 4 = 120. Since the sample space size is 216,
P(B) = 120/216 = 5/9
Final Computation
Using conditional probability:
we substitute P(AB) = 1/12 and P(B) = 5/9:
P(A|B) = (1/12) / (5/9) = (1/12) × (9/5) = 9/60 = 3/20
Thus, the probability that the sum of the three dice is 10 given all three dice differ is 3/20.
Quick Verification with a Program
We can quickly verify with a short Python code that enumerates all possible ordered outcomes of three dice, then checks the conditions.
count_AB = 0
count_B = 0
for i1 in range(1, 7):
for i2 in range(1, 7):
for i3 in range(1, 7):
# Check if all distinct
if i1 != i2 and i2 != i3 and i1 != i3:
count_B += 1
# Check if sum is 10
if i1 + i2 + i3 == 10:
count_AB += 1
p_AB = count_AB / 216
p_B = count_B / 216
p_A_given_B = p_AB / p_B
print(p_AB, p_B, p_A_given_B)
You will see that p_AB = 1/12, p_B = 5/9, and p_A_given_B = 3/20, confirming the theoretical result.
Possible Follow-Up Questions
Why do we consider permutations (ordered triples) instead of combinations (unordered)?
When dealing with dice rolls, each die is a distinct entity (Die 1, Die 2, Die 3). The outcome (1, 3, 6) is different from (3, 1, 6) for instance, so we must count these permutations separately in the sample space. If we used combinations, we would lose track of the ordering and get an incorrect count.
Could we have computed P(A) or P(B) differently?
Yes. For P(B), an alternative approach is to note that the probability of the first two dice being different is 5/6, and then the probability that the third die also differs from the first two is 4/6, so P(B) = (5/6) × (4/6) = 20/36 = 5/9. This matches the counting argument.
For P(A) (the probability that the sum is 10 without any condition), we can list all ordered triples i1, i2, i3 that sum to 10, but it’s simpler to do that enumerating or applying combinatorial methods. However, we specifically need P(A|B) in this question, so the direct route using P(AB) and P(B) is more straightforward.
What if the dice were not fair?
If the dice were unfair (biased), the uniform probability assumption (each outcome having probability 1/216) would not hold. We would need the probability distribution of each face roll and sum over all distinct outcomes accordingly. The formula P(A|B) = P(AB)/P(B) still applies in principle, but P(AB) and P(B) would be computed using the biased probabilities.
How could this logic be extended to more dice or different sums?
The same general process applies: define the desired event (such as the sum being a particular value) and the conditioning event (dice all different, or any other condition), then calculate P(AB)/P(B). For a larger number of dice or a different sum, combinatorial enumeration can be more cumbersome, so we often resort to dynamic programming or generating functions to systematically count or sum over the probabilities.
What is the intuition for the result 3/20?
Given that the dice are all distinct, we are restricting ourselves to a subspace of 120 equally likely outcomes. Of these 120, exactly 18 yield a sum of 10. Thus 18/120 = 3/20. This fraction is 0.15, meaning there is a 15% chance of having a sum of 10 among all-distinct outcomes.
Below are additional follow-up questions
What if we accidentally include cases where dice outcomes repeat while computing P(AB)?
A common pitfall is to miscount the favorable outcomes for AB when the dice must all be distinct. For instance, someone might list out all triples summing to 10, forget to exclude those with repeated values, and thus inflate the count of favorable outcomes. This leads to an incorrect probability.
To avoid this, one must carefully separate sums that use repeated faces, such as (4,3,3), from those where the three faces are all distinct, like (1,4,5). A systematic approach is to first find all unordered triples that sum to 10 with distinct values, then multiply each unordered triple by 3! to account for permutations. Any triple that has duplicates or all the same values is excluded in this distinct-values scenario.
In the real world, could the result be different if the dice are not physically identical?
In theory, if the dice were physically distinguishable (e.g., different weights or manufacturing defects) but still fair, mathematically each outcome remains equally likely. However, in practice, very slight asymmetries can introduce small biases. If all dice have different design imperfections, you could see a tiny deviation in probabilities.
For practical purposes, as long as the dice remain “statistically fair,” each of the 216 outcomes can be treated as equally probable. But in strict real-world scenarios, dice can deviate from ideal fairness in ways that are not uniform across dice. To correctly compute the probability, you would need to estimate or measure each die’s distribution of faces, then incorporate those into your calculation for both the sum and the distinctness conditions.
Could there be a scenario where we only observe partial information (for example, we only see two dice) and want to compute a similar conditional probability?
Yes. Suppose you see the first two dice and you want to compute the probability of the sum being 10 given that these two dice are different. The problem then partially changes: you now know two dice are different and you know their values, so you need the distribution for the third die conditioned on the existing partial outcome.
For instance, if the first two dice show (3,4), then you want the probability that the sum becomes 10 (meaning the third die is 3) given that the third die is different from 3 and 4. However, in that conditional scenario, the third die cannot be 3 or 4 anymore if you maintain the “all distinct” condition. You would have to properly account for the new constraint.
A key pitfall is to forget that the event “third die is different from the first two” only leaves 4 possible faces for the third die. Hence you recalculate carefully with updated constraints, ensuring you do not incorrectly assume 6 potential faces for the third die.
How do we handle a general sum S if we want to compute the probability that the dice sum to S given they are all different?
The key idea generalizes: you first find all distinct triples (i1, i2, i3) that sum to S. Each unordered triple of distinct faces can be permuted in 3! ways. You then divide the total count of these valid permutations by 6×5×4 (the total number of ways to roll three distinct faces).
One subtlety is ensuring that S is within the feasible range for distinct dice: the smallest distinct sum is 1+2+3=6 and the largest distinct sum is 4+5+6=15. If S is outside 6 to 15, the probability is zero under the “all distinct” constraint. A typical pitfall is forgetting to check for sums that are not possible with distinct values (e.g., sum of 3 with three dice is not possible unless dice repeat).
What if a player re-rolls dice that match and only stops rolling when all dice are different? Does that affect the probability?
This is a different scenario, essentially introducing a conditional process: the player continues rolling any dice that repeat until the three dice are all distinct. The question then becomes a matter of analyzing a repeated trial process until event B (all dice different) is achieved. Once B is achieved, we check if the sum is 10.
This might seem like the same as P(A|B), but it subtly shifts the distribution of how the final distinct triple is arrived at. Each re-roll step has a certain probability distribution for distinctness. If we eventually settle on a distinct triple, the path to that triple can affect the probabilities if there are any biases introduced by the re-roll mechanism. In a memoryless scenario with truly fair dice, you can argue that once we “arrive” at a distinct triple, it is equally likely to be any of the 120 distinct permutations. Thus under the assumption of memoryless and fair dice, the probability remains the same 3/20. However, it’s crucial to confirm that no additional biases were introduced by the re-roll rule (for instance, if re-roll attempts are limited or if a certain face is replaced more often).
How would you verify your manual counting if you only had partial code or computational power?
A risk arises if we run a code sample that loops over all 216 possible outcomes but mistakenly counts only unordered sets or forgets to handle repeated outcomes. For partial checks or more constrained resources, one could:
Break the problem down into smaller checks (e.g., first confirm how many ordered triples sum to 10, then how many among them have distinct faces).
Use carefully crafted test cases that verify edge scenarios, such as sums at the boundary of possible distinct sums (like 6 and 15).
Compare manual enumerations for small slices (e.g., let i1=1, then vary i2, i3) to confirm that results match expectations.
These mini-tests reduce the chance of incorrectly skipping or double-counting outcomes under resource constraints. A subtle pitfall is mixing up the roles of indices or forgetting about certain ordered combinations.
How does the concept of conditional probability here relate to Bayesian updating?
In Bayesian terms, observing that the dice are all distinct (event B) updates our “prior” distribution over sums to a “posterior” distribution conditioned on B. Formally, you might say that before learning B, the sum distribution is uniform over the 216 outcomes (with some sums more likely than others). After observing B, our new sample space shrinks to 120 equally likely distinct outcomes.
A classic pitfall is to assume that the knowledge of “dice are distinct” does not change the relative likelihood of different sums. But in fact, it does: Some sums are more heavily reliant on duplicates (e.g., sum=12 includes combinations like (4,4,4)), so the conditioning on distinct outcomes changes which sums remain feasible and how likely they are in that subspace. Properly applying conditional probability is the essence of the Bayesian perspective here: the prior distribution is replaced by the posterior once new evidence (event B) is observed.
What if we wanted the maximum-likelihood sum given that the dice are all different?
This question shifts to: among all triple-distinct outcomes, which sum is the most frequent? We would have to count, for each sum S from 6 through 15, how many distinct permutations yield that sum. The sum with the highest count is the most likely under the condition B. For example, sum=10 has 18 such outcomes, but perhaps sum=9 or sum=11 might have more distinct permutations. One must systematically verify these counts (like sum=9: distinct sets could be {1,2,6}, {1,3,5}, {2,3,4}, each with 3! permutations).
A subtlety is ensuring the counting is accurate. If a person miscounts or overlooks a combination, they might incorrectly identify the most frequent sum. To avoid this pitfall, you could write a small program that enumerates all 120 distinct outcomes and tally which sums they produce.
What if the dice are not six-sided (e.g., 8-sided or 10-sided dice)? Is the logic the same?
Yes, the logic of conditional probability is the same, but the counting changes:
For n-sided dice, the total ordered outcomes are n^3.
The number of ways to have three distinct outcomes is n × (n-1) × (n-2).
The sum you target may have a wider range (minimum is 1+2+3 = 6, maximum is (n-2) + (n-1) + n = 3n - 3 if you require all distinct).
You would enumerate or find all distinct triples summing to the target and then compute probability accordingly.
A subtle pitfall is forgetting to adapt the counting when the dice are not standard six-sided dice. Many people will keep using 216 in the denominator or use 3 sets of permutations from the six-sided case, leading to an incorrect result. The principle remains the same, but the enumerations must be carefully recalculated for n-sided dice.
How might rounding or floating-point precision impact the final probability calculation in software?
When implementing these calculations in floating-point arithmetic (e.g., Python’s float), tiny rounding errors can cause your printed result to deviate slightly from 3/20. For instance, you might see 0.14999999999 or 0.150000000002. This is natural in finite-precision floating-point arithmetic.
A pitfall is assuming that a tiny discrepancy from 0.15 invalidates the result. Instead, you should confirm that the difference is within machine epsilon or a small tolerance. When exact rational arithmetic is needed, you could use Python’s fractions.Fraction or symbolic math libraries to confirm the exact fraction 3/20.