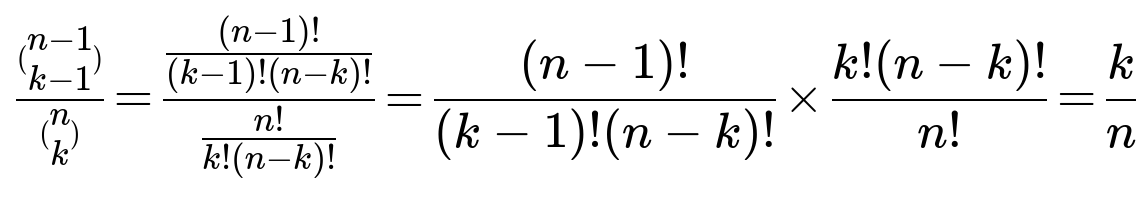ML Interview Q Series: Conditional Probability & Combinatorics: First Coin Toss Heads Given k Total Heads
Browse all the Probability Interview Questions here.
A fair coin is tossed n times. Given that there were k heads in those n tosses, what is the probability that the first toss was heads?
Solution Explanation
To understand this probability, consider the condition that out of n tosses of a fair coin, exactly k are heads. We want the conditional probability that the very first toss is a head, given the total count of k heads in all n tosses.
Combinatorial Reasoning
Plugging these into the ratio:
Example Code to Illustrate Through Simulation
Below is a short Python simulation that provides empirical evidence for the above result. It simulates many trials of n tosses, counts how many heads were observed, and checks how often the first toss was heads when exactly k heads appeared.
import random
import math
def simulate_probability(n, k, trials=10_000_00):
count_first_head_given_k = 0
count_k_total = 0
for _ in range(trials):
tosses = [random.choice(['H', 'T']) for _ in range(n)]
total_heads = sum(1 for toss in tosses if toss == 'H')
if total_heads == k:
count_k_total += 1
if tosses[0] == 'H':
count_first_head_given_k += 1
if count_k_total == 0:
return 0
return count_first_head_given_k / count_k_total
n = 10
k = 4
estimated_probability = simulate_probability(n, k)
theoretical_probability = k / n
print(f"Estimated probability: {estimated_probability}")
print(f"Theoretical probability: {theoretical_probability}")
Real-World Connection
In practical scenarios such as analyzing user events, performing a Bayesian inference on successes in a sequence, or looking at outcomes over multiple draws, this concept reaffirms the idea that if we condition on the total number of successes, each trial shares an equal chance of being a success. This is particularly important when building or interpreting partial-information models.
Additional Detailed Reasoning for Interview Depth
Below are additional follow-up questions
If the coin's probability of landing heads changed partway through the sequence (i.e., it was not the same for all n tosses), would that affect the probability that the first toss was heads given k heads in total?
When the probability of heads changes at some point mid-sequence (for example, if the coin was fair for the first x tosses and then biased for the remaining n−x tosses), the tosses would no longer be exchangeable. Exchangeability is crucial to our original reasoning. Under the condition that there are k total heads, the location of those heads is no longer symmetric across the n tosses if some tosses come from a different probability distribution.
In that scenario, the probability that the first toss is heads—conditioned on seeing k heads out of n total tosses—could differ from k/n. One would need additional information about when exactly the probability changed, the prior distribution of heads for each time segment, and the total number of heads contributed by each segment to derive the correct conditional probability. For instance, if the coin was fair for the first half and strongly biased for the second half, you would need to account for the fact that more heads are likely concentrated in the segment with the higher bias. That changes how likely the first toss (which belongs to the “fair” segment) is to be among the heads, given you know there are k in total.
A potential pitfall is assuming independence and identical distribution over the entire sequence. If that assumption is broken, the straightforward k/n conclusion no longer holds. You must carefully compute or model the conditional probability by enumerating or integrating over all possible ways the heads can be distributed across the segments where the coin’s bias differs.
What if we only know that there are k heads, but we do not know the exact number of tosses n? Could we still determine the probability that the first toss was heads?
If you do not know the total number of tosses n, you lack a key piece of information needed to make the standard combinatorial argument. In other words, to say the first toss is heads with probability k/n, you need to know both k (the total heads) and n (the total tosses). If n is unknown but k is known, then there is ambiguity regarding how many tails might have been tossed overall.
You could attempt a Bayesian approach where you place a prior on n and incorporate the information that there are k heads overall. Even then, you might need to consider how you came to know there are k heads without knowing n. This is a tricky scenario: one possibility is that you observed each toss and counted heads, but somehow lost track of the total number of tosses. Another possibility is that you only observed the heads, but not the tails, so your knowledge is partial.
Without a distribution or prior assumption on n, you cannot compute a well-defined probability. If you do have a prior P(n) for the total number of tosses, you would need to sum or integrate over all possible values of n, weighting by how likely each n is given that there are k heads total. Only then could you arrive at the posterior probability of the first toss being heads. This scenario highlights how critical it is to have complete information about n to apply the simple ratio k/n.
Could the probability that the first toss was heads change if we observed partial sequences, for example, if we only saw the first m tosses (but still know the total k heads in all n tosses)?
Observing a partial sequence can indeed alter our conditional probabilities. Suppose n tosses occurred, you know there are k total heads, and you observed the outcomes of the first m tosses (where 1 < m < n). Let’s say, for instance, you saw the outcomes for the first m tosses and among those m tosses, r of them were heads. Now the question “What is the probability that the first toss was heads?” given (1) the total of k heads in n tosses and (2) that among the first m tosses, r were heads, is more nuanced.
We must reframe the problem with updated information:
The event that the first toss was heads might be correlated with how many heads you saw in the subsequent m−1 tosses that you observed, because these partial observations constrain the distribution of remaining heads among the remaining tosses.
In principle, you could use a combinatorial argument again but with extra conditions. Specifically:
Condition on both “the total number of heads is k” and “the first m tosses contain exactly r heads.”
Then ask: in how many of those configurations is the very first toss a head?
Divide by the total number of configurations consistent with those conditions.
The ratio might still end up simplifying (often it does because of symmetry and exchangeability within the unobserved tosses), but you need to be careful. If you directly observe that the first toss was tails in that partial observation, then the question is moot (probability is zero). If you do not specifically observe the first toss’s outcome (maybe you observed tosses 2 through m, but not toss 1) while still counting that there were r heads in the first m tosses, then the first toss being a head or tail is still an exchangeable scenario with the constraint of r total heads among the first m. But the presence of partial knowledge about the sequence can break naive symmetry in certain complicated setups.
If we are told that exactly k heads occurred, but we also know the first toss was tails, how does that modify the probability that the second toss was heads?
This scenario focuses on a shift in which toss we are interested in once we have partial information about the first. Initially, if we only know that there are k heads in total, each toss is equally likely to be heads at probability k/n. But once we learn that the first toss was tails, we now know there are still k heads, but they must lie in the remaining n−1 tosses. Therefore, the question becomes: “What is the probability that the second toss is heads given that the first toss was tails and we have k total heads among all n tosses?”
Here is how to think about it:
A subtle pitfall is to forget that learning the first toss was tails changes how the heads are distributed. You must condition correctly on that new piece of information. Another subtlety is that the question is about the second toss specifically, not the first. After you have the knowledge that the first toss is tails, the second toss is symmetrical with the remaining n−1 tosses. If the second toss had also been revealed to be tails, you would then conclude that there are still k heads left among n−2 tosses, altering the probability for the third toss, and so on.
How would the reasoning differ if we had a sequence of coin tosses where outcomes were not independent but had some correlation structure (for example, a Markov chain)?
When outcomes are correlated, the probability of seeing certain patterns of heads or tails depends on the outcomes of previous tosses. If you have a Markov chain of order 1, for example, the probability that the i-th toss is heads depends on whether the (i−1)-th toss was heads or tails. Consequently, the enumerations of sequences that contain exactly k heads are not all equally likely unless the chain structure still somehow preserves exchangeability (which is unusual for standard Markov chains).
Thus, the naive formula k/n for the probability that the first toss is heads—given you ended up with k heads total—generally does not hold. In a correlated environment, to find “the probability the first toss was heads given that there are k heads in total,” you would have to use the joint probability model that accounts for the transitions:
Enumerate all possible sequences of length n with k heads.
Weight each sequence by its actual probability under the Markov transition probabilities.
Sum the probabilities of those sequences where the first toss is heads.
Divide that sum by the probability of having k heads in total.
This can be done analytically for small n or specialized Markov chain structures, but it may become computationally intensive for large n. A real-world pitfall is to assume i.i.d. and apply k/n in a scenario where correlation is present (for instance, if the coin “tends to repeat” the previous outcome with a certain probability).
If we tried to build a confidence interval for the probability that the first toss is heads, given partial data about the sequence, how would we approach it?
Constructing a confidence interval for a conditional probability can be tricky, especially if the distribution is not purely i.i.d. or if you do not observe the entire sequence. Nonetheless, one approach for building a confidence interval might be:
Define a parametric or nonparametric model for how the k heads could be distributed among the n tosses.
Use maximum-likelihood estimation or a Bayesian approach to estimate the probability that the first toss is heads under the condition that the total is k heads.
If you have repeated trials of the entire process, you could empirically estimate the fraction of times the first toss is heads among all sequences with k total heads and then form a confidence interval around that empirical fraction.
If you rely on the standard i.i.d. Bernoulli assumption with known probability (like a fair coin p=0.5), the distribution is well-defined, and the exact answer is k/n for all sequences that have k heads in n tosses. However, if there are unknown parameters (like an unknown bias p) or correlated tosses, you must factor that uncertainty into the confidence interval calculation. A big pitfall is ignoring the variability of the underlying model and incorrectly stating that the conditional probability is k/n when p is unknown or the tosses are correlated.
What if there is a possibility of measurement error (i.e., we might have miscounted heads or tails)? How would that affect the calculation?
If we may have miscounted the total number of heads, k, or if there is uncertainty in the classification of each toss (for example, a sensor incorrectly reads a tail as a head sometimes), then the event “we have exactly k heads in the sequence” is itself uncertain. Our knowledge of k might be subject to error.
In practice:
We might have a probability distribution for “observed k” given the “true k.”
We need to incorporate that measurement error in any probability calculation about the location of heads.
Hence, “the probability that the first toss was heads given that we observed k heads” would become:
But to evaluate that, we might need to consider all possible “true k' ” weighted by the likelihood of observing k from k'. If the measurement errors are small and random, the intuitive result might be close to k/n. However, large error rates or systematically biased sensors could significantly shift the probability, since some sequences are more likely to be miscounted as having k heads than others. A major pitfall is to assume perfect knowledge of k when real measurement processes might produce mistakes.
If we repeated the experiment multiple times with different values of n and k, how could we verify empirically that the probability is k/n?
To empirically verify the result, we could perform a Monte Carlo experiment along these lines:
Decide on a range of n values (for example, n = 5, 10, 20).
For each n, sample many thousands of sequences of coin tosses from a fair coin (p=0.5).
Record each sequence’s total heads.
Partition the sequences by the total head count k (from 0 up to n).
Within each partition of sequences that has exactly k heads, count how many of those sequences have the first toss as heads.
Compute the ratio of “first toss heads” sequences to the total sequences in that partition.
Compare this ratio to k/n.
Over large numbers of trials, the empirical ratio should converge to k/n if the coin is truly fair and if each toss is i.i.d. A subtlety is that if you combine multiple values of n in a single dataset, you have to separate them carefully by their k and n to see that the ratio for each (k, n) pair is close to k/n. Another subtlety is if the coin is not exactly fair or if there is correlation or measurement error, the empirical ratio might deviate systematically from k/n, and that deviation would be evidence of a mismatch from the standard i.i.d. fair coin assumption.
How does the concept of exchangeability extend if we have a mixture of different coins but do not know which coin is tossed at each step?
If we have a mixture of different coin biases (like one coin with probability p1 for heads, another coin with probability p2, and so on), but for each toss we randomly choose which coin to flip (or we have a bag of coins but do not track which one is used for each toss), the overall process can be considered a “mixture distribution” of Bernoulli trials.
Whether or not the tosses are exchangeable depends on how the selection of coins is performed:
If each toss is made by randomly drawing from the same mixture distribution of coins with a fixed probability for picking each coin, then the sequence is i.i.d. from the mixture distribution. In that case, all tosses are identically distributed, though they come from a mixture. You still get exchangeability in the sense that each toss has the same marginal probability of heads. Conditioned on the total k, the probability that any particular toss (including the first) is heads can still be shown to be k/n by a symmetry argument across tosses.
However, if the selection of which coin to use changes in a systematic or known pattern (for example, the first half of tosses always uses coin with p1, the second half uses coin with p2), then tosses are no longer exchangeable. The probability that the first toss is heads given k total heads across all tosses would not necessarily be k/n in that scenario.
A pitfall is to treat the mixture scenario incorrectly as a single fair coin. If the mixture is unknown or complicated, the data might suggest an effective overall “p,” but the distribution of heads among toss positions could be skewed if certain coins are used more often at certain times. Thorough analysis demands clarity on how the coins are chosen at each toss.
Could knowledge about k heads in consecutive segments of the tosses change the probability for the first toss?
Yes, if you know more detailed information about how many heads appeared in certain segments of the toss sequence, that might constrain the possible configurations in ways that break the simple exchangeability across the entire sequence.
For example, if you know “out of the first half (n/2 tosses), there were k1 heads, and out of the second half, there were k2 heads, with k1 + k2 = k,” then the probability that the very first toss (which is in the first half) was heads is now conditional on the fact that the first half collectively has k1 heads. Because the first half itself is constrained, a direct combinatorial argument focusing only on that segment is typically used:
Within the first half, there are k1 heads. Then the probability the first toss is heads among those first n/2 tosses is k1 / (n/2) (if the coin is i.i.d. for that segment and we are looking only at the first half’s distribution).
Meanwhile, the second half has k2 heads. That separate piece of information does not directly alter the probability that the very first toss is heads, except that it ensures the entire sequence has k heads in total.
A subtle real-world pitfall is to treat partial segment data incorrectly, leading to confusion about whether the probability k/n still applies. Once you subdivide the sequence into segments, you might need to recast the problem in terms of “Given we know how many heads are in the segment containing the first toss, is the first toss heads?” That might lead to a ratio k1 / (n/2), not k/n, because the relevant sample space is only those tosses in the first segment.
What happens if we had a prior that each toss could also land on a side (like the coin lands and sticks on its edge) with some tiny probability? Does that affect the result?
If there is a third outcome—Heads (H), Tails (T), or Edge (E)—then we are no longer dealing with a standard Bernoulli or binary outcome. Suppose the coin can land on its edge with probability ε, heads with probability (1−ε)/2, and tails with probability (1−ε)/2, or some variant of these probabilities. If we specifically condition on the event “There are k heads in total,” does that automatically exclude the possibility of some tosses landing on edge? Not necessarily. The total of k heads can occur alongside some number of edges.
We might reframe the question to specify that we only count H vs. T, ignoring the edge outcome, or we might say we are only looking at sequences with exactly k heads and ignoring how many edges. In either case, if edges are possible, the combinatorial distribution changes. The probability that the first toss is heads, given that exactly k heads occurred, will generally not be k/n because not all toss outcomes are equally likely in a purely two-outcome sense. The presence of a third outcome breaks the standard binomial distribution assumption.
To do the calculation rigorously, you would need the probability model for heads/tails/edge, the total number of tosses n, and how many times the coin landed on edges in addition to those k heads. Then you count or weigh the sequences that have k heads among n tosses, possibly with some number of edges. The fraction that have the first toss as heads might or might not simplify to k/n, depending on how the edges factor in. A subtle pitfall is ignoring the contribution of edges, effectively forcing a binomial viewpoint when the actual distribution is multinomial.
How might we approach an algorithmic challenge where we need to quickly compute the probability that the first toss was heads across many different values of n and k?
def probability_first_head_given_k(n, k):
return k / n # Valid for i.i.d. coin tosses
No heavy computation is required. This is a big advantage in a scenario where an interviewer might say, “How could you handle a million queries for different n and k efficiently?” The pitfall is that if you misunderstand the distribution (i.e., the coin isn’t fair or i.i.d., or there is measurement error), you might supply an incorrect formula. Always confirm the assumptions hold in your real-world or interview problem.
In a real production setting, how can we confirm that the coin tosses are indeed i.i.d.?
Verifying i.i.d. assumptions in real data can be non-trivial. In practice, one might:
Perform a runs test (a statistical test that checks whether heads and tails occur in clusters more often than expected under independence).
Estimate the autocorrelation of the binary series across various lags to see if heads are systematically followed by heads (or tails) more than chance.
Check if the probability of heads changes over time (drift in p), or if different coins or flipping mechanisms cause different biases.
If these tests show no significant deviations, you can more confidently assume i.i.d. behavior. The big pitfall: many real processes that appear “coin toss-like” can have hidden correlations—like a mechanical bias in the flipping method that might become more pronounced as physical conditions change. If your verification step indicates correlation or time-varying bias, you cannot rely on the simple k/n result for “probability that the first toss was heads.”
Suppose we want to generalize from coin tosses to random variables with more complex distributions, but we still want to know the probability that the first draw took a certain value given the total number of occurrences of that value. Does a result analogous to k/n hold?
For discrete random variables with multiple categories, the same style of reasoning can hold if the draws are i.i.d. and we condition on how many times a certain category appears in the entire sample. Specifically, if you have a discrete random variable X that takes values in {1, 2, …, m} with some probability distribution, and you condition on “the number of occurrences of category j is k out of n,” the probability that the first draw was in category j is indeed k/n under exchangeability.
Why? Because each arrangement of the draws that has exactly k occurrences of category j is equally likely (under an i.i.d. assumption). Out of those k occurrences, picking which positions in the sample are category j is a purely combinatorial choice with symmetrical weighting. Therefore, each position is equally likely to be among the k occurrences. The pitfall is forgetting that i.i.d. is essential: if the draws are not i.i.d. (e.g., Markov chain or another dependency structure), you lose that straightforward combinatorial symmetry.
What if the coin toss was physically performed in a biased manner, but the final data we receive is re-weighted or corrected in some way? Does that affect the probability?
If a physical coin flip is biased, but then someone or some device attempts to “correct” the bias by discarding or weighting certain outcomes to produce an effectively uniform distribution of heads and tails across the final reported dataset, you have to be very careful. The final reported data might appear to have exactly k heads out of n tosses, but the process by which those tosses are selected or weighted can break the simple view that each arrangement of k heads is equally likely. The selection or weighting scheme can introduce dependencies among tosses.
For instance, if the system discards sequences that exceed a certain threshold of heads or tails, or if it re-samples partial outcomes, that can systematically alter how likely each arrangement of heads is. The probability that the first toss is heads, given exactly k heads in the final curated data, might deviate from k/n because the curation process does not treat each toss identically. This scenario frequently arises in data engineering pipelines: always check if the data has been preprocessed or filtered in a way that removes or biases certain sequences. That would be a hidden pitfall if one directly applies k/n without understanding the data pipeline.
How might the question differ if we look for the probability that the first two tosses were both heads, given there were k heads in total?
This is another extension that frequently arises in interviews: we might ask about multiple specific positions. If we want the probability that the first two tosses were heads, given that there were k heads in total among n tosses, we can do a similar combinatorial or symmetry argument:
for i.i.d. coin tosses. Simplifying the binomial coefficient ratio yields:
The logic is straightforward once you see the pattern. It also aligns intuitively with the idea that, out of k heads among n tosses, the chance that any specific pair of positions (like the first two) are both heads is the fraction of heads pairs in all positions. A pitfall is to guess the probability might be (k/n)^2 if you are thinking about unconditional probabilities in an unconditioned Bernoulli process. But you must do a precise combinatorial argument given that you already know exactly k heads are present.
If the tosses have some unknown distribution, how can we proceed with a non-parametric approach?
In a non-parametric approach, we do not assume a specific functional form for the coin’s probability distribution. Instead, we might rely on the principle of exchangeability or the observed data directly. For instance, if we have a large number of repeated experiments (each with n tosses) and we observe the fraction of experiments that have k total heads and also the fraction of those that have the first toss as heads, we can empirically estimate:
(\hat{P})(first toss is heads | k heads in n tosses) = (# of runs with k heads and first toss = heads) / (# of runs with k heads)
“(\hat{P})” here means we are estimating (from observed data or simulations) the probability that the first toss is heads given there are (k) heads total in (n) tosses.
We would not assume a binomial distribution or a Markov model. Instead, we let the data speak for itself. If the unknown distribution is truly exchangeable, the results should converge to k/n. If it is not exchangeable, we will get some other value. The challenge is having enough data to reliably measure these probabilities for each k. A subtle pitfall in a non-parametric setting is limited sample size. For large n, the number of runs with exactly k heads could be small, so the estimate may be noisy. This highlights the interplay between theoretical derivations and real data constraints.
What if the coin is fair, but we do not have perfect knowledge that it is fair? Could that lead us to a different posterior probability for the first toss being heads?
If we are uncertain whether the coin is truly fair, we might place a prior over the coin’s bias p (for instance, a Beta(α, β) prior). After observing that there are k heads out of n tosses, we could update our belief about p using Bayes’ theorem:
Now, the question “What is the probability that the first toss was heads?” can be interpreted in a Bayesian sense. However, if the coin tosses are truly i.i.d. with an unknown p, once we condition on exactly k heads, each of the n tosses is again exchangeable within that observation. The posterior predictive probability that a specific toss was heads, given that there are k heads in total, remains k/n for the standard Beta-Binomial model.
One subtlety is that the question “Was the first toss heads?” is about a past event, not a future toss. So we might think of it as a posterior probability for a latent event given a summary statistic k. The exchangeability argument still applies to the latent events. So even under a Beta prior for p, if the tosses are exchangeable and we only know the summary (k heads in n tosses), the probability that the first toss was heads is k/n. A major pitfall is to confuse the posterior predictive probability of a future toss being heads with the posterior probability that a specific past toss was heads. For a future toss, the probability is (k+α)/(n+α+β) in a Beta-Binomial framework. But for a specific past toss, given that exactly k heads appeared among all n, the probability is k/n.
How could this problem appear as part of a more complex puzzle in interviews?
One common twist: an interviewer might first ask for the probability that a particular toss is heads if there are k heads in total, to see if you realize the answer is k/n (or a generalization for multiple positions). Next, they might embed that result in a more elaborate puzzle involving partial reveals, dynamic updates, or tricky conditioning events. For example, “We show you the outcome of the last toss is heads, the total heads is k, and one random toss from the first n−1 is also heads. Now what is the probability the very first toss was heads?” Each new condition modifies the counting or weighting of sequences. The fundamental principle—exchangeability plus correct conditioning—still underlies any correct solution.
A subtle pitfall is to jump to an unconditioned probability or to apply the standard k/n formula without carefully checking that the new conditions do not break the uniform weighting across configurations.
How could we confirm exchangeability if we only observed a single sequence of length n and know that it has k heads?
Observing just one sequence of n tosses that yields k heads is typically insufficient to statistically confirm that every arrangement of k heads is equally likely. You would need repeated experiments or some well-founded prior knowledge about the fairness and independence of the coin tosses. If you only have one sequence, you can’t verify the distribution of possible outcomes. You would typically rely on physical arguments (fair coin, standard flipping mechanism) or theoretical assumptions. Without repeated data or physical justifications, you cannot confirm exchangeability from a single sequence. A pitfall is to claim that seeing one sequence with k heads “proves” that the probability the first toss was heads is k/n. Rather, the combinatorial argument for k/n depends on the i.i.d. assumption. Observing exactly one outcome of that process doesn’t test that assumption in a robust statistical sense.
Would it make a difference if the coin toss results were revealed to us in real time, or if we only see the final tally of k after all tosses are completed?
If we see the results in real time, we are not simply conditioning on “k heads in total” in the abstract sense. We might gain partial knowledge along the way, which changes our perspective on the distribution of future outcomes or even on the question about the first toss if we somehow momentarily forget it. However, if at the end we forget the entire sequence except for the knowledge that there were k heads in total, then from that final vantage point, all sequences with k heads are again equally likely from the perspective of an observer who only retains that one statistic. The difference is that, in the real-time reveal, we might have used partial knowledge to update our beliefs after each toss. But if the question is strictly, “Given k heads in total, what is the probability the first toss was heads, ignoring any memory of intermediate reveals?” then real-time knowledge does not matter unless we keep it in the final conditioning.
A subtle real-world scenario: If you do keep partial knowledge from real-time observation, you might not remain in the symmetrical scenario that drives the simple k/n outcome. For instance, if you already know that the first toss was heads from real-time observation, the question is trivial (probability 1). Or if you know partial outcomes of the first half, that changes your posterior distribution about how the remaining heads are distributed. A pitfall is mixing partial real-time observations with final aggregated data incorrectly, losing the purely combinatorial viewpoint.
Does the solution work if we are dealing with infinite sequences and only know the proportion of heads in the limit?
In an infinite sequence scenario, saying “there were k heads out of n tosses” for infinite n is not a standard event. You might talk about the limiting frequency of heads as n goes to infinity. If you interpret the question in a limiting sense—like “Given that the empirical frequency of heads is p, what is the probability that the first toss was heads?”—it becomes a different question. For an exchangeable infinite sequence (like a de Finetti process), the limiting frequency of heads is almost surely a certain random value. Even then, conditional on that limiting value being p, by exchangeability, each toss is as likely as any other to be heads. The formal measure-theoretic arguments would show that the probability the first toss is heads is p if you condition on the entire infinite sequence having a proportion p of heads. A pitfall is incorrectly applying finite combinatorial arguments to an infinite sequence. One must rely on de Finetti’s theorem or other measure-theoretic approaches for infinite exchangeable sequences.
If the result is k/n for a fair coin, can we create a simple simulation to illustrate the difference when the coin is not i.i.d.?
Yes, you can. For a non-i.i.d. coin, you might define a small Markov chain with states “Heads” and “Tails” and a transition probability matrix:
# Example of a simple Markov chain
# Prob of H->H is 0.8, H->T is 0.2, T->H is 0.2, T->T is 0.8
import random
def next_toss(current_toss):
if current_toss == 'H':
return 'H' if random.random() < 0.8 else 'T'
else:
return 'H' if random.random() < 0.2 else 'T'
Then simulate many sequences of length n:
Start with a random toss for toss 1 (say heads or tails with 50-50 chance).
For each subsequent toss, use the Markov transition probabilities.
Count how many sequences yield exactly k heads.
Among those sequences, count how many have the first toss as heads.
Compare that empirical ratio to k/n.
You will typically see a deviation from k/n because the correlation structure influences which sequences are more or less likely. This highlights a real-world pitfall: if a process is not truly i.i.d., a naive combinatorial argument can be misleading.
If we suspect a trick in the question—like the statement “given that there were k heads in those n tosses” actually came after we saw the first toss was heads—would that alter the analysis?
If you first observe that the first toss is heads, and then someone states “it turns out there were k heads in total,” you must incorporate that knowledge. Now, you already know the first toss was heads, so the probability that the first toss was heads is 1 by direct observation. The question might be moot. However, if you are only told about k heads in total after the entire experiment, without prior knowledge of the first toss, the standard argument stands.
Another subtle scenario is if the question is poorly worded and the timing of knowledge is ambiguous. If the condition that there are k heads is only established after seeing that the first toss was heads, your interpretation of probability changes. The pitfall is to conflate unconditional knowledge with knowledge gained sequentially. In an interview, clarifying when the condition is applied is crucial. The canonical interpretation is that you discover the total k heads afterward without prior knowledge of individual outcomes.
What if each head is worth a certain reward, and you want to know the expected payoff from the first toss?
If each head is worth R units (and tails is worth 0), then the expected payoff from the first toss, given there are k heads total out of n, is R times the probability the first toss is heads under that condition. Because that probability is k/n (for i.i.d. fair coin tosses), the expected payoff from the first toss is:
If we consider n tosses with k heads as a random sample from the binomial distribution, is there an intuitive short proof that each toss is equally likely to be among the k heads?
One short intuitive argument is:
You pick any one toss at random (for example, the first toss).
Because the n tosses are i.i.d., there is no reason for that toss to have a different distribution from any other.
Conditioned on the event that there are k heads in total, you effectively labeled k of the n tosses as heads. By symmetry, each toss is equally likely to be one of those k.
Hence the probability that any single toss is heads (given the total is k) is k/n. The pitfall is ignoring that this argument hinges on identical distribution across tosses and uniform weighting of all sequences with k heads. If that uniform weighting is broken, the intuitive “pick any toss at random” argument also breaks down.
If the question asked for a joint probability, such as the probability that the first toss was heads and the last toss was heads, would it still be k/n?
No. That is a different question. The probability that the first toss and the last toss are both heads, given k heads total, involves the number of sequences with the first toss as heads and the last toss as heads, among all sequences with k heads. Specifically:
If an interviewer asks, “Could you provide an alternative explanation using symmetry without relying on binomial coefficients?” how might you respond?
A purely symmetry-based argument might go like this:
Suppose you label each toss from 1 to n.
You are told that exactly k of these labels are associated with heads.
All labelings that place k heads among n labels are equally likely because the coin is fair and the tosses are i.i.d.
Therefore, from the perspective of someone who only knows k but not which tosses are heads, each label has an equal chance of being one of the k heads.
The chance that label 1 (the first toss) is one of those k is k/n.
You never even explicitly used binomial coefficients in that explanation. A pitfall is to assume this argument automatically generalizes to correlated or time-varying probability scenarios; it does not. However, for i.i.d. fair coin tosses, it is perfectly valid.
How can we connect this problem to machine learning or data science settings?
In a classification setting, imagine you have n samples, and exactly k of them are labeled “positive.” If the labeling is i.i.d. and we treat the positions of the positive labels as exchangeable among the n samples (no features, purely random labels), then the probability that any particular sample (for instance, the first sample in the dataset) is positive given that k of them are positive is k/n. This is akin to the coin toss problem. It is a simplistic model for random labeling.
However, in real data science contexts, the labels are rarely purely random. Features can correlate with the label. The dataset might not be i.i.d. or might be drawn from a process with hidden structure. The pitfall is to oversimplify real labeling processes as random tosses. The exchangeability principle does not hold if the label generation process depends on sample features in a systematic way. This draws a parallel to the “coin toss not truly i.i.d.” scenario.
If someone tries to interpret the question in a frequentist testing scenario, how might they set it up?
A frequentist might imagine repeatedly performing the experiment of tossing a fair coin n times and recording how many heads appear. Over many such experiments, they would collect all experiments in which k heads were observed. Within that subset, they would count how many had the first toss as heads. By the law of large numbers, as the number of experiments grows, the fraction that have the first toss as heads will converge to k/n. This is exactly the frequentist interpretation of the conditional probability.
Potential pitfalls in a testing scenario include small sample sizes, measurement errors, or hidden biases. If any of these exist, the observed fraction may deviate from k/n. A real data approach also has to consider that perfectly fair coins and perfectly independent tosses are theoretical ideals.
Is there a scenario in which someone might incorrectly derive 1/2 as the answer?
A common incorrect assumption is: “The coin is fair, so the probability of heads for any single toss is 1/2, no matter what.” That is the unconditional probability for each toss if you do not know anything else. However, the question specifically says you know that there are k heads in total out of n tosses. That changes the sample space from all possible sequences of n tosses to only those sequences that contain k heads. Within that conditioned space, each position does not simply have an unconditional 1/2 chance of being heads. Instead, each position is equally likely to be among the k heads, making the probability of heads for a given position (like the first toss) k/n. A pitfall is forgetting that conditioning on the total number of heads restricts the sample space in a way that changes the probability.
If someone tries to combine partial knowledge of k and some prior guess that the first toss was heads, is that valid?
Combining partial knowledge is valid only if you carefully apply conditional probability rules. For instance, if you initially guess that the first toss is heads with probability 1/2 (prior to seeing the total of k heads), and then someone tells you that there are k heads among n tosses, you can apply Bayes’ theorem:
If we suspect the coin is fair but the data shows a strong deviation from k/n, what might that indicate in a real experiment?
If repeated empirical data shows that, given k heads in n tosses, the first toss is heads at a rate significantly different from k/n, it might indicate:
A problem in the randomization procedure (e.g., the first toss might be systematically influenced by how the coin is flipped).
The coin or environment might not be i.i.d.
The coin might have a hidden bias that only manifests on the first toss (like an unbalanced position from which it is flipped).
Potential data-collection or measurement issues.
A pitfall is to ignore that large deviations in actual data from the theoretical ratio could be a sign of a deeper problem. For example, if you keep flipping the coin from the same initial orientation every time, maybe the first toss is more likely to land heads than the subsequent ones.
Could the reasoning be extended to a scenario where we care about the rank order of the heads (for example, the probability that the first head occurs on toss number j given k total heads)?
It typically won’t simplify to something as clean as k/n for j>1, but the combinatorial approach is the same. The subtlety is that the question about the location of the first head is different from asking if a specific toss is heads. A pitfall would be to guess a uniform distribution over all toss positions for the first head, which is not correct because the first head can’t appear after k heads have already occurred, and we know there are exactly k in total.
What if the tosses are not distinct or labeled? Does that even make sense?
If tosses are unlabeled (or if someone scrambles the order of results so we only see a “multiset” of H and T), then talking about “the first toss” is ambiguous. The combinatorial argument to identify “which position is heads” relies on labels for each toss (1 through n). If the tosses were physically performed but then scrambled in time, we can’t even define “the first toss was heads” in a meaningful chronological sense. In that scenario, you might define “the first toss” as the first in some random ordering, or you might define it as “the earliest in time,” but if you truly scramble them so there is no distinct earliest toss, the question is ill-defined. A subtle real-world scenario: if you only see aggregated results (k heads, n−k tails) with no ordering, you cannot meaningfully ask about the “first toss.” A pitfall is failing to clarify what “first” means in a scrambled scenario.
If k equals n/2 for an even n, some might argue the answer must be 1/2. Why is that incorrect?
If n is even and k=n/2, one might jump to the naive conclusion that the probability that the first toss is heads is 1/2 because the coin is fair and k/n = (n/2)/n = 1/2 anyway. That actually does match k/n. So for k = n/2, 1/2 is indeed the correct probability, but you need the combinatorial reasoning or the exchangeability argument to confirm it. If you guess “1/2” simply because the coin is fair in an unconditional sense, you might accidentally be right for the wrong reason. For k = n/2, the correct reasoning is that each position has an equal share in the k heads out of n. The pitfall is that for other values of k, the probability is not 1/2.
Could the question ask for a short proof that “knowing the total number of heads does not affect the uniform distribution over positions for those heads?” What would that proof look like?
Does the question remain unchanged if someone re-labels the tosses in reverse order, or in any permutation?
No matter how you label or relabel the tosses, if the coin tosses are i.i.d. and fair, the set of sequences with k heads among n tosses remains the same. The positions are just a relabeling of time steps. As long as you remain consistent in how you define “first toss” after relabeling, the probability for it being heads is the same by symmetry. A potential pitfall is to think that changing the labeling or perspective might change the probability. It does not, as long as the process is symmetrical. The notion of a “first toss” is arbitrary under a symmetry argument, but typically we label them in chronological order.
If an interviewer challenges you to show the reasoning in a single line or minimal step, how might you respond?
Does this result help in deriving the expected value of the number of heads in the first m tosses?
Yes. Using linearity of expectation and symmetry, if there are k heads in total among n tosses, the expected number of heads in the first m tosses is:
This is just scaling the probability that any one of those m positions is heads (k/n) by m. A subtle pitfall is to assume that all positions in the first m are heads or all are tails. You must apply linearity of expectation carefully. Another nuance is that this is the expected count given that there are k heads total, not the unconditional expectation.
In advanced mathematics, how does de Finetti’s theorem relate to this scenario?
De Finetti’s theorem states that an infinite sequence of exchangeable Bernoulli random variables can be represented as a mixture of i.i.d. Bernoulli sequences with some parameter p. That means if you know the sequence is exchangeable, then it is “as if” you first sample a random p from some distribution, and then condition on that p, the sequence is i.i.d. Bernoulli(p). For the finite question, “Given that there are k heads in n tosses, what is the probability that the first toss was heads?” exchangeability at finite n is enough to guarantee the k/n result if no other constraints or correlations are introduced. The pitfall is to disregard that exchangeability is itself a strong assumption. De Finetti’s theorem simply provides a deeper foundation for why, under exchangeability, each toss is equally likely to be the head among the total k, in an infinite or finite context.
If the question included an extra condition like “the last toss was definitely heads,” does that break the probability for the first toss?
If you also know that the last toss was heads, then among the k heads, one is definitely assigned to position n (the last toss). That means there are k−1 heads left to be distributed among the first n−1 tosses. So the probability that the first toss is heads given k total heads and a known head on the last toss is:
So it changes from k/n to (k−1)/(n−1) because we used up one head in the last position. A classic pitfall is forgetting to recondition on that new piece of information.
Is there a geometric or intuitive visualization that might help?
Could a random walk perspective create confusion about the first toss?
Yes. In a random walk perspective, you might track the difference between heads and tails as you progress from toss 1 to toss n. Then “having k heads total” means that after n steps, the random walk has a certain final value (k heads minus n−k tails = 2k−n). The first toss being heads corresponds to the random walk starting at +1. One might incorrectly try to analyze the random walk path distribution under that endpoint condition. However, unless you are careful, you can get lost in the complexities of path constraints. The simpler combinatorial argument that each path with k heads is equally likely leads you back to k/n for the first toss. A pitfall is to treat the random walk viewpoint incorrectly as if the path shape might discriminate the first toss, ignoring the fact that all path shapes are still equally likely among those with k heads.
Could repeating the question with multiple coins lead to a multi-dimensional extension?
If you had multiple coins tossed side by side, say coin A is tossed n times and coin B is tossed n times, and you only know that the total heads for all tosses from both coins is K (some combined total). Then the question “What is the probability that coin A’s first toss was heads?” becomes more complicated. You need to consider how those K heads are split across the two sequences of n tosses each, for a total of 2n tosses. If you have no prior reason to believe that coin A’s tosses are less or more likely to be heads than coin B’s tosses (and all 2n tosses are i.i.d. from the same distribution), you might do a combinatorial argument across 2n positions. The pitfall is to forget that coin A is not necessarily distinguished from coin B except in labeling. If they truly are the same coin or distribution, each of the 2n tosses is equally likely to be among the K heads. But if coin A is physically different or done at different times, that might break the uniform assumption.
Could there be a relationship to gambler’s ruin problems or negative binomial questions?
While gambler’s ruin and negative binomial problems often focus on the distribution of the count or the number of successes before a certain event, they do not directly ask “Which toss was heads?” under the condition of k total heads. They revolve around different conditioning events, like “We stop when we have k heads” or “We stop when the total surpasses some threshold.” The direct question about the probability that the first toss was heads given a total of k heads typically remains a simpler combinatorial argument for i.i.d. fair coin tosses. A pitfall is conflating gambler’s ruin (where the process ends at a boundary) with this scenario (where we are not stopping early but looking at a fixed n).
Would the statement still be valid if the coin is tossed infinitely, but we only look at the first n tosses where exactly k heads occur?
If we have an infinite series of tosses and we somehow pick out the first n tosses that contain exactly k heads (like a stopping rule that says “Keep tossing until we have recorded k heads, plus some extra tosses?”), the subset of tosses might not be i.i.d. or exchangeable because the selection mechanism could be nontrivial. For instance, if we only look at the first n tosses once we observe k heads in them, that is conditioning on a complicated event in the infinite process. It is not the same as simply saying “We have a fixed block of n tosses, and it has k heads.” The probability that the first toss in that block is heads can be skewed by the stopping procedure. A pitfall is to treat those two scenarios as identical. They are not.
Could the question appear as a puzzle about “k winners in a lottery among n participants, what’s the probability that participant #1 was a winner?”
Yes, that is an equivalent statement in a different context. If you have n participants in a lottery, k winners are randomly chosen out of n. If participant #1 is as likely to be chosen as anyone else, the probability that participant #1 is among the k winners is k/n. This is an exact analog to “which toss is heads.” A subtle pitfall is to do a direct ratio argument, incorrectly concluding 1/2 for a fair coin, forgetting that the total number of heads is restricted to k. The correct analogy with lottery winners is that each participant is equally likely to be among the k winners. This is a helpful real-world illustration.
In large-scale computations, might floating-point inaccuracies in computing binomial coefficients be an issue?
Could the question be re-labeled for “what is the probability the coin landed heads on any specific toss i, given k heads in total?”
Yes. By symmetry, the answer is the same for any toss i, not just the first. The probability that toss i is heads given that there are k heads out of n is also k/n. There is nothing special about i=1 under the i.i.d. assumption. The pitfall is to treat the first toss differently from others, thinking it might have a different distribution if you physically observe it first. In a purely theoretical scenario, or after the fact, all tosses are symmetrical.
If someone only studied average outcomes, could they miss the result?
If you only look at unconditional averages like “the expected number of heads in n tosses,” you get n/2 for a fair coin. That does not directly address the conditional probability question. You need to specifically condition on the event that there are k heads in total. A pitfall is to conflate unconditional probabilities or expectations with the conditional case. Interviews often test whether a candidate recognizes the difference between unconditional and conditional reasoning.
Could we interpret the question as an example of the principle of insufficient reason or the principle of indifference?
Yes. The principle of indifference states that if all outcomes are equally likely and you have no reason to favor one over another, assign them equal probabilities. Given no reason to believe one particular toss is more likely to be heads among the k total heads, you distribute that likelihood uniformly across all n tosses. That yields k/n. This is effectively a philosophical viewpoint behind exchangeability. The pitfall is to apply the principle of indifference incorrectly when the scenario is not truly uniform or has additional constraints.
If we tried to prove it formally by induction on n, could that be done?
One might do an induction proof on n:
Base case: For n=1, if k=1, probability is 1 that the first toss (the only toss) is heads. That equals k/n. If k=0, probability is 0. So it holds.
Inductive step: Assume it holds for n−1. For n tosses with k heads, partition sequences by whether the first toss is heads or tails. Then show it must be k/n. The details can mirror the binomial coefficient argument. A pitfall is that some might find the combinatorial argument simpler than a formal induction. Both are correct approaches in mathematics.
Could the question appear in a Bayesian updating scenario about an unknown chance of heads, then we only see the total k heads, and we want the posterior distribution of which tosses are heads?
Yes. In a fully Bayesian scenario with unknown p, once you condition on k total heads, each toss is symmetrical under the i.i.d. assumption. The posterior distribution across all configurations with k heads is uniform among those configurations. Then the marginal posterior probability that a particular toss is heads is k/n. The pitfall is to incorrectly attempt to do a direct posterior on p first, then guess about individual toss outcomes. You must handle the entire joint distribution carefully. The uniform distribution over the positions of heads emerges from exchangeability and the binomial likelihood.
Suppose the problem asked for the probability that the first toss was tails, given that k heads appear in n tosses. Is there any difference?
Could a question about partial replacement or partial knowledge after some tosses be relevant?
Yes. For example, if you toss the coin n times, observe all outcomes but then “lose” the record of the first toss but remember the total number of heads, do you still compute the probability the first toss was heads as k/n? Indeed you do, because from your perspective, the first toss is unknown, while you still know the total is k. That is basically the same scenario: you only have partial knowledge of the entire sequence. A pitfall is to think you can glean more from your memory if you “sort of recall some partial pattern.” That might break the symmetrical argument unless your memory is truly just “the total k.”
Could any interviewer ask about the continuous-time analog, like a Poisson process?
In a continuous-time setting, you might have events that arrive according to a Poisson process with some rate λ. If exactly k events occur in the interval [0, T], what is the probability that an event occurred in the sub-interval [0, t]? By the properties of the Poisson process, the arrival times of the k events are i.i.d. uniform in [0, T] once you condition on there being exactly k events. Thus, each event is equally likely to be in any sub-interval of length t. The probability that an event landed in the first sub-interval is t/T. That is analogous to our discrete scenario. The pitfall is mixing up discrete tosses with continuous arrivals, but the principle of “uniform distribution among events” is quite similar.
Does the question remain instructive in typical ML or data science interview contexts?
Yes, absolutely. Many data science tasks revolve around partial knowledge or partial observation. This coin toss puzzle tests a candidate’s grasp of conditional probability, combinatorial reasoning, and exchangeability—fundamental concepts that recur in more advanced ML topics. A candidate who can fluidly discuss the pitfalls, hidden assumptions, and how to handle real-world uncertainties shows the depth of understanding that top companies value. A pitfall for interviewees is to present a correct formula (k/n) without demonstrating they understand when it applies or how to adapt if assumptions are violated.