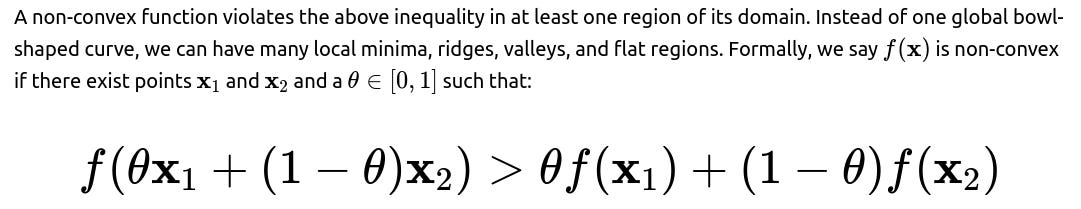ML Interview Q Series: Convex vs. Non-Convex Cost Functions: Optimizing Machine Learning Models.

📚 Browse the full ML Interview series here.

26. Explain the difference between convex and non-convex cost functions. What does it mean when a cost function is non-convex?

A convex cost function, in the context of optimization and machine learning, is one for which any line segment between two points on its graph lies entirely above or on the graph. Equivalently, a function is convex if, for every pair of points in its domain, it satisfies the convexity inequality. This property is extremely valuable because it guarantees that any local minimum is also the global minimum. Optimization in convex problems is often more straightforward since gradient-based algorithms or other convex optimization techniques will converge reliably to the global optimum.

A non-convex cost function is one that does not exhibit this property. When a cost function is non-convex, it can have multiple local minima, local maxima, and saddle points. There is no guarantee that a local minimum found by gradient-based methods is the absolute lowest point. Neural networks, for example, usually have non-convex cost landscapes due to the many parameters and nonlinear activations. Despite the potential challenge of numerous local minima or saddle points, modern practice has shown that even in these highly non-convex setups, it is often possible to find good minima that generalize well.

Understanding the geometry is crucial. In a convex function, you can imagine a “bowl” shape (though in many dimensions), whereas a non-convex function might look more like a mountain range, with many peaks and valleys. If the cost function is non-convex, optimization often involves careful choice of learning rates, initializations, and possibly advanced techniques like momentum, adaptive learning rates, or regularization. These methods help navigate the complex terrain and avoid getting stuck in poor local minima or plateaus.

Convex Cost Function

This means the function evaluated at a convex combination of two points is never larger than the same convex combination of the function evaluated at those points. In a high-dimensional setting, a convex function will have a single global optimum. Gradient descent in a strictly convex problem will reliably converge to the unique global solution. Classic examples of convex cost functions in machine learning are the squared error cost for linear regression or logistic loss for logistic regression (where the optimization w.r.t. the linear parameters is convex).

Non-Convex Cost Function

When a cost function is non-convex, it means there is no guarantee that a local minimum is the global minimum. This is typical in deep neural networks because the mappings from inputs to outputs are highly nonlinear, especially when many layers and parameters are involved. Despite this, practical techniques have shown that many neural network losses contain broad flat minima that generalize well, and standard optimizers like stochastic gradient descent can find regions of good performance.

Why Non-Convex Functions Arise in Machine Learning

The moment we introduce nonlinearities, especially from deep learning architectures (such as ReLU or sigmoid activation functions, or more complicated building blocks like LSTM cells), the parameter space and the resulting objective function become non-convex. Feature interactions in polynomial expansions, certain kernel methods, or any method with hidden units will typically yield non-convex optimization landscapes.

Neural networks with many layers and large numbers of parameters almost always have non-convex loss surfaces. Even simpler multilayer perceptrons, with just a single hidden layer, are non-convex with respect to the weight parameters. While this may sound daunting because it complicates optimization, empirical evidence and theory about wide networks suggest that local minima often perform comparably well in terms of generalization on real-world data, as long as careful training techniques are employed.

Non-Convex Cost Functions in Practice

In practice, optimizing non-convex cost functions requires heuristics, careful engineering, and hyperparameter tuning. Techniques include:

Choosing suitable weight initialization strategies (e.g., Xavier/Glorot initialization or He initialization). Using advanced optimizers (e.g., Adam, RMSProp, AdaGrad, or Adadelta) that adapt learning rates. Applying momentum or variations like Nesterov momentum to help escape shallow local minima or saddle regions. Using appropriate regularization and architectural choices, such as dropout, batch normalization, or skip connections, that can help shape the loss landscape. Selecting batch sizes and data shuffling strategies that can sometimes help avoid poor local minima or saddle points.

While non-convex cost functions lack the comforting global optimality guarantees of convex ones, current deep learning success is in large part due to the fact that local minima found by standard gradient-based methods can still lead to highly accurate models in practice.

Scenario Where This Matters

In simpler tasks such as linear regression or logistic regression without hidden layers, you have a convex cost function. In this scenario, a closed-form solution or a standard gradient descent approach is guaranteed to find the global optimum. But once you move to complex deep neural networks, the cost function inevitably becomes non-convex. Understanding these differences helps you decide on optimization strategies and interpret training convergence behavior.

Potential Pitfalls

With non-convex functions, practitioners must be aware of local minima, saddle points, and the potential for the training process to stall. Sometimes the landscape is dominated by saddle points rather than local minima, which can cause extremely slow convergence. Plateaus in high-dimensional surfaces are also a serious concern. This is why monitoring training metrics, adjusting learning rates, or employing learning rate schedules (like cosine annealing or step decay) can be vital. It is also crucial to note that hyperparameter settings that work for one non-convex setup might not transfer to another, especially in extremely large-scale neural network architectures.

Example Code Snippet in Python

Below is a small illustrative example of a non-convex cost function encountered when training a simple neural network in PyTorch. This is just to demonstrate how one might define the cost function and network. The cost function in the example, while it looks standard (e.g., cross entropy for classification), is non-convex with respect to the network’s weights.

import torch
import torch.nn as nn
import torch.optim as optim

# Simple feed-forward network with one hidden layer
class SimpleNet(nn.Module):
    def __init__(self, input_dim, hidden_dim, output_dim):
        super(SimpleNet, self).__init__()
        self.fc1 = nn.Linear(input_dim, hidden_dim)
        self.relu = nn.ReLU()
        self.fc2 = nn.Linear(hidden_dim, output_dim)

    def forward(self, x):
        x = self.fc1(x)
        x = self.relu(x)
        x = self.fc2(x)
        return x

# Instantiate the network
model = SimpleNet(input_dim=10, hidden_dim=20, output_dim=2)

# Define a non-convex cost function (standard cross entropy for classification is non-convex in weights)
criterion = nn.CrossEntropyLoss()

# Optimizer (e.g. Adam)
optimizer = optim.Adam(model.parameters(), lr=0.001)

# Example training loop
data = torch.randn(5, 10)  # 5 samples, 10-dimensional input
labels = torch.randint(0, 2, (5,))  # binary targets

# Forward pass
outputs = model(data)
loss = criterion(outputs, labels)

# Backward pass
optimizer.zero_grad()
loss.backward()
optimizer.step()

print("Loss:", loss.item())

Even though cross-entropy or mean-squared error might be convex in the outputs (logits) themselves, as soon as you consider them with respect to the neural network parameters, the objective is non-convex.

Below are some important follow-up questions that a FANG-level interviewer might ask. Each one reveals deeper layers of knowledge about convex vs. non-convex optimization in machine learning.

What is the significance of convexity in optimization, and why is it so highly valued?

Convexity simplifies optimization considerably. In a strictly convex problem, any local minimum is guaranteed to be the global minimum. This property ensures that gradient descent or other algorithms like Newton’s method converge consistently to the same global optimum regardless of initialization. From a theoretical standpoint, convex optimization offers strong convergence guarantees, well-developed duality theories, and simpler analyses of performance bounds.

However, many real-world tasks require more expressive models such as neural networks. These become non-convex in their parameters, but the additional representation power often outweighs the downside of losing convexity guarantees. In practice, the improved expressiveness of non-convex models can capture complex relationships in the data that simpler convex models cannot.

If I have a neural network, is its cost function typically convex or non-convex?

Neural networks almost always produce non-convex cost functions with respect to their parameters. The presence of nonlinear activation functions like ReLU, tanh, or sigmoid, plus interactions among multiple layers, creates a highly non-convex loss landscape. While the final form of the cost function (for instance, cross-entropy for classification) might appear straightforward, combining it with neural network parameters leads to a very high-dimensional, non-convex surface.

In standard feed-forward networks with a single hidden layer, the cost function is already non-convex, and for deeper or more complicated networks like CNNs, RNNs, or Transformers, non-convexity is even more apparent. This means in principle that standard gradient-based training methods can get stuck in local minima or saddle points. However, empirical results show that many local minima are effectively “good enough” and lead to high accuracy.

Why do neural networks often use non-convex cost functions, and isn't that a problem for optimization?

Neural networks naturally introduce non-convex cost functions because of the layered, nonlinear transformations. The composition of linear layers and nonlinear activations allows deep networks to learn extremely sophisticated functions. It is precisely these nonlinearities and parameter interactions that yield powerful feature extraction and decision boundaries.

This can indeed create challenges for optimization since global guarantees are lost. But in practice, large-scale gradient descent variants have proven surprisingly effective at navigating these landscapes. Research in deep learning suggests that, in sufficiently high-dimensional spaces, local minima are not typically isolated sharp pits but can be wide basins that generalize well. While there are no formal guarantees that you always find the global optimum, standard heuristics, improved initialization methods, careful learning-rate schedules, and large-scale data all help in finding solutions with strong performance.

What happens if a non-convex cost function has many local minima? How do we handle it?

Many local minima do exist, but not all local minima are equally problematic. One important perspective from research in deep learning is that local minima with higher training losses can sometimes be escaped more easily due to the geometry of high-dimensional surfaces or noise introduced by stochastic gradient descent. Other times, the minima found are “good enough” solutions that yield competitive performance, especially on real-world data.

Techniques to handle local minima include:

Using momentum-based optimizers (SGD with momentum, Adam, etc.) that can push through small local minima. Scheduling learning rates so that they begin large enough to leap over narrow local minima and later reduce to refine the final solution. Adding noise (either inherent in stochastic mini-batch updates or explicit regularization) can help the model escape shallow local minima or saddle points. Using modern network architectures (like residual networks, skip connections, or normalization layers) that empirically yield friendlier loss landscapes.

In short, while local minima can be a theoretical concern, in practice, many well-chosen architectures and optimization strategies rarely get stuck in extremely poor minima for most mainstream tasks.

Are gradient-based methods guaranteed to find the global optimum in a non-convex cost function?

They are not guaranteed in a strict mathematical sense. Gradient-based methods like SGD can converge to local minima, saddle points, or sometimes just very slowly improving regions, especially if the landscape has many plateaus. The success in deep learning does not come from formal proofs that we always reach the global minimum. Instead, it comes from empirical findings that indicate solutions discovered by these algorithms tend to be good local minima or wide basins with near-optimal performance, at least on the training distributions and tasks that are typical in practice.

In research contexts, some results show that under certain conditions (like very wide networks or specific architecture constraints), almost all local minima can yield similarly good performance. But these results do not provide universal guarantees across all possible neural architectures.

Could we convert a non-convex problem to a convex one in practice?

It is theoretically possible in certain restricted scenarios. Kernel methods, for instance, can map data into very high-dimensional feature spaces, and the resulting optimization in that feature space can sometimes be convex in terms of the kernel parameters. However, for deep neural networks, the transformations and architecture choices typically make the entire mapping non-convex. Attempting to turn the entire network training problem into a convex one often destroys the representational advantage that made deep networks attractive in the first place.

Methods like convex neural networks, certain forms of shallow networks with convex regularizers, or other special architectures have been researched, but they have not seen widespread adoption compared to standard non-convex deep networks. The general trade-off is that enforcing convexity can limit the model’s flexibility and performance.

Are second-order methods relevant for non-convex cost functions?

Second-order optimization methods involve the Hessian matrix of second derivatives. In a non-convex problem, the Hessian can have both positive and negative eigenvalues and might be very costly to compute or approximate accurately in high dimensions. Some approximate second-order methods like L-BFGS can be used for small to medium size problems, but for large-scale deep learning tasks, they become computationally expensive in both memory and compute time.

Nevertheless, there are some limited settings where second-order or quasi-Newton methods can be beneficial. Researchers have proposed methods like K-FAC (Kronecker-Factored Approximate Curvature) that approximate the Hessian for deep networks. These approaches can yield faster convergence under certain conditions, but their complexity often limits their adoption in extremely large-scale settings.

Does batch size or data distribution matter for convex vs. non-convex cost functions?

The shape of the overall cost function with respect to the parameters remains non-convex regardless of batch size or data distribution. However, the stochastic nature of mini-batch updates can help with escaping local minima or saddle points by injecting noise into the gradient estimates. Large batch sizes reduce this noise but sometimes lead to different generalization properties and can cause the optimizer to converge to sharper minima if not carefully managed. Very small batch sizes have more gradient noise, potentially helping exploration but also making training unstable. Data distribution also affects the local geometry of the cost surface because certain subsets of data can highlight or obscure certain directions of descent.

Show me a scenario in code where we experiment with a simple convex function vs. a non-convex function.

import numpy as np
import matplotlib.pyplot as plt

def convex_function(x):
    return x**2

def non_convex_function(x):
    return x**2 * np.cos(x)

def gradient_descent(f, df, init_x, lr=0.01, steps=100):
    x_values = []
    fx_values = []
    x = init_x
    for _ in range(steps):
        x_values.append(x)
        fx_values.append(f(x))
        grad = df(x)
        x = x - lr*grad
    return x_values, fx_values

# Derivatives
def d_convex_function(x):
    return 2*x

def d_non_convex_function(x):
    return 2*x*np.cos(x) - x**2*np.sin(x)

# Run gradient descent on both
init_x_convex = 5.0
init_x_nonconvex = 5.0

convex_x_vals, convex_fx_vals = gradient_descent(convex_function, d_convex_function, init_x_convex)
nonconvex_x_vals, nonconvex_fx_vals = gradient_descent(non_convex_function, d_non_convex_function, init_x_nonconvex)

# Plot results
plt.figure(figsize=(12,5))
# Plot for convex
plt.subplot(1,2,1)
x_range = np.linspace(-6, 6, 300)
plt.plot(x_range, convex_function(x_range), label='convex x^2')
plt.plot(convex_x_vals, convex_fx_vals, 'ro-', label='GD path')
plt.title('Convex Function x^2')
plt.legend()

# Plot for non-convex
plt.subplot(1,2,2)
x_range = np.linspace(-6, 6, 300)
plt.plot(x_range, non_convex_function(x_range), label='non-convex x^2 cos(x)')
plt.plot(nonconvex_x_vals, nonconvex_fx_vals, 'ro-', label='GD path')
plt.title('Non-Convex Function x^2 cos(x)')
plt.legend()

plt.show()

Could regularization turn a non-convex loss into a convex one?

Typical regularizers, such as L2 or L1 weight penalties, do not fundamentally turn a non-convex problem into a convex one when combined with a neural network. Instead, they can alter the shape of the loss landscape, potentially smoothing it or reducing the amplitude of certain undesirable minima, but they do not generally restore convexity once there are multiple layers and nonlinear activations involved. The overall objective remains non-convex but might become more tractable, reducing overfitting and sometimes providing better minima.

Final Thoughts on Convex vs. Non-Convex

A cost function is convex if it satisfies the property that any local minimum is a global minimum. For linear or simple machine learning models, this often applies, which makes training straightforward. A non-convex cost function, common in neural networks and more complex modeling paradigms, can have multiple local minima, saddle points, and other complexities in its loss landscape. Despite the theoretical challenges, modern deep learning is built on non-convex losses and yet succeeds in practice due to high-dimensional optimization phenomena, robust optimizers, and large datasets.

---

Below are additional follow-up questions

Can combining multiple cost terms — some convex and some non-convex — lead to an overall convex cost function?

When we sum or otherwise combine multiple cost components, the overall cost function is convex only if all of the components are convex and they are combined via operations that preserve convexity. If any term in the sum is non-convex, the result is generally non-convex.

One subtle point is that even if a cost function looks like a sum of multiple parts (e.g., a convex regularizer like L2 plus a data-fitting term that is non-convex in the parameters), the presence of any non-convex element typically makes the entire cost non-convex.

For example, suppose you have:

• A convex regularization term

  

  A data-fitting term

  f(w)

  that is non-convex in the parameter vector w

Then the combined objective is:

Even though

is convex, if

f(w)
is non-convex, the sum

J(w)

remains non-convex. One typical scenario is a neural network with weight decay. The weight decay term is convex (it is simply

), but the main cost (e.g., cross-entropy with respect to deep neural network weights) is non-convex, so the final objective is non-convex.

In practice, many training objectives in machine learning have a convex term (often for regularization) plus a non-convex term (due to the model structure), resulting in a non-convex objective overall. The non-convexity may pose theoretical challenges, but practitioners typically accept it for the modeling power gained by non-linear structures.

Does the choice of activation function in a neural network directly affect convexity or non-convexity of the overall cost function?

Yes, the activation function greatly influences whether the resulting parameter mapping is convex or non-convex with respect to the network parameters. Generally, any non-linear activation (e.g., ReLU, sigmoid, tanh, etc.) introduces non-convexity. The cost function for a linear regression or logistic regression with a purely linear model (no hidden layer) is convex w.r.t. parameters, but once we add even a single layer with a ReLU or sigmoid activation, the cost becomes non-convex.

To illustrate why, consider a single-hidden-layer neural network:

where

σ

is a non-linear activation function (e.g., ReLU, sigmoid). Even if we use a convex loss in terms of

(like mean-squared error or cross-entropy with respect to logits), the dependence on

is non-convex due to the non-linear activation.

Hence, the cost surface ends up having many local minima and saddle points. If we replaced

σ

with the identity function, the mapping would be purely linear in the parameters, leading to a convex cost. But that would forfeit the expressive power of neural networks, which is precisely due to the non-linearities.

Is it possible for a cost function to be convex over some regions of parameter space and non-convex over others?

Yes. A function can be piecewise convex and piecewise non-convex, or more generally, it might exhibit convex behavior in specific local neighborhoods but not across the entire domain.

In many high-dimensional loss landscapes, certain regions may look “bowl-shaped” locally, and gradient-based methods might behave as if the function is approximately convex in that region. However, if you move into a different region of the parameter space, the function might show non-convex behaviors with multiple local minima or ridges.

An example is a neural network with piecewise linear activations such as ReLU. In any region where the ReLU units do not switch their on/off states, the network behaves like a purely linear mapping (hence, convex in that slice), but across boundary regions where some ReLU units switch states, the overall function changes form and can become non-convex globally.

In practice, you cannot rely on local convexity to guarantee a global optimum, but local convexity can sometimes simplify the training trajectory if the optimizer remains in a region that appears to be “nicely” behaved.

Are there scenarios where a model's cost function looks convex when viewed as a function of certain variables, but is non-convex in the full parameter space?

Yes. Many machine learning models, including matrix factorization and neural networks, can look convex when viewed in one subset of variables while holding another subset fixed, but become non-convex once you consider all parameters jointly.

A classic example is matrix factorization. The problem of factoring a matrix

M

into product of two matrices

U

and

V

can be convex if we fix one of the factors; we might see a simpler, convex least-squares cost in the other factor. But if both factors are variables, the combined problem is non-convex.

Similarly, in neural networks, if you freeze all layers except the last one, optimizing the final layer’s weights with respect to a convex loss (like cross-entropy on linear logits) is convex. Once you include earlier layer parameters in the optimization, the objective is non-convex because of the non-linear transformations.

This partial convexity property leads to techniques like alternating minimization, coordinate descent, or block coordinate descent, where we alternately optimize over subsets of parameters. While this can be efficient in certain contexts, it does not transform the overall problem into a globally convex one.

What are some subtle convergence issues that can arise in non-convex training when using advanced optimizers like Adam or RMSProp?

When using adaptive gradient methods such as Adam or RMSProp on non-convex cost functions, a few subtle issues can arise:

• Sensitivity to learning rate schedules. Adam can appear robust, but in certain non-convex cases, an overly large learning rate might skip over narrow but good minima or cause the parameters to bounce between basins of attraction. Too small a learning rate might trap the network in a wide plateau or cause very slow convergence.

• The phenomenon of “sharp minima vs. flat minima.” Adaptive methods sometimes allow the network to settle into sharper local minima, which could affect generalization. In non-convex cost functions, the geometry of the region around the local minimum matters. Sharp minima might yield higher test error even if the training error is low.

• Potential mismatch between training phases. If you change from one optimizer to another mid-training (e.g., from Adam to SGD), the transitions can cause abrupt changes in the exploration of the loss surface. This can be beneficial or detrimental depending on how it is orchestrated.

These subtle points emphasize the importance of careful hyperparameter tuning, momentum coefficient selection, and an awareness of the underlying geometry of the loss.

Could the dimensionality of the parameter space help or hurt finding good minima in a non-convex cost function?

High dimensionality can paradoxically help in finding “good enough” solutions. In very high-dimensional parameter spaces, local minima may be connected by broad valleys or there might be an abundance of “degenerate” minima that perform similarly well. Some research in deep learning suggests that in extremely high dimensions, the probability of encountering truly bad local minima is relatively low in practice.

However, high dimensionality can also cause:

• Exploding or vanishing gradients in certain architectures or parameter ranges, potentially making it harder to navigate the cost landscape. • A proliferation of saddle points or flat plateaus that slow down convergence. • Increased complexity in hyperparameter search, since more parameters often require more careful tuning of learning rate schedules, initialization, and regularization.

Overall, while high dimensionality can present challenges, it also seems to allow neural networks more flexibility to “slide around” the landscape and find acceptably good regions of low loss in practice. This interplay between dimensionality and non-convex optimization is still an area of active research in theory and practice.

How do we evaluate “success” in training when we cannot guarantee finding a global optimum in a non-convex problem?

In real-world machine learning tasks, especially with deep networks, success is usually measured by generalization performance on a validation or test set, rather than by strictly finding the global optimum of the training loss. Even if an algorithm converges to a local minimum, that local minimum may generalize well if it is a “flat” or “broad” minimum.

Some practical metrics for evaluating success are:

• Validation set accuracy (or any relevant metric, such as F1 score, precision, recall, etc. for classification tasks). • Test set accuracy or error, checking for overfitting or underfitting. • Robustness to distribution shifts. Sometimes a local minimum might be good on the training set but performs poorly if data shifts slightly. • The shape of the loss landscape around the final parameters: flatter minima can correlate with better generalization.

Thus, the objective in practice is not necessarily to find the absolute global minimum of the training loss; it is to find a region in parameter space that yields strong performance on unseen data.

In what ways can ensemble methods mitigate the challenges of non-convex cost functions?

Ensemble methods often help in non-convex scenarios by combining predictions from multiple models, each of which might be stuck in a different local minimum or trained under different conditions. Some practical ways ensembles help:

• If each model is independently initialized and trained, they will likely land in different local minima or different regions of the non-convex landscape. Averaging or voting across these models can smooth out idiosyncrasies or errors from any one model’s local optimum.

• Ensembles can improve generalization by leveraging the diversity in learned decision boundaries. Even if each model is non-convex, the combination can be more robust to specific local minima quirks.

• In practice, methods like snapshot ensembling or model checkpoint ensembling collect multiple snapshots of the model during the training process (e.g., at different epochs or learning rate schedules) and average them. This effectively reduces the variance introduced by non-convex training paths.

Although ensembling does not solve the fundamental non-convexity, it mitigates potential overfitting and local irregularities. The downside is increased computation time and memory usage since multiple models or multiple snapshots must be stored and executed at inference time.

What is the difference between a strictly convex function and a strongly convex function, and how does that differ from a general convex function in the context of optimization?

• A function is convex if for all

and for any

θ∈[0,1],
it satisfies:

• It is strictly convex if:

for

and

θ∈(0,1).

Strict convexity ensures that there is a unique global minimum, so you cannot have multiple different points in the domain all attaining the same minimum value unless they coincide.

• It is strongly convex if there exists a constant

μ>0
such that for all

and

θ∈[0,1],

Strong convexity ensures an even stronger form of uniqueness for the optimum and leads to faster convergence rates for gradient-based methods (often linear or exponential convergence for algorithms like gradient descent in finite-dimensional problems).

In practical optimization (like linear or logistic regression with L2 regularization), the loss can become strongly convex, which yields robust and fast convergence. However, most neural network objectives do not satisfy such properties because of non-linearities. Hence, the powerful convergence guarantees of strongly convex or strictly convex functions typically do not apply to typical deep neural network training.

Could partial convexity in some layer parameters be exploited to speed up training of a non-convex model?

Yes. In certain architectures, we can sometimes isolate a subset of parameters that define a convex sub-problem, then optimize them separately in a more direct or closed-form manner. Methods like “alternating least squares” in matrix factorization exploit this idea. Another example: in neural networks, if you keep hidden layers fixed and only retrain the final linear classification layer, that portion is convex with respect to that last layer’s weights.

Some meta-learning or optimization frameworks try to “unwrap” non-convex layers or approximate them to gain partial convexity, then iterate. While this can help, it typically does not yield a fully convex problem. Even so, it may improve training stability or speed for certain tasks, especially if the partially convex portion is large enough or critical enough in shaping the final model output.

One has to be aware that the final, end-to-end optimization remains non-convex, but partial convex sub-steps can reduce complexity in practice, especially if combined with careful layer-freezing or block-wise updates.

Can non-convex cost functions become easier to optimize under certain transformations, such as normalizing or scaling inputs?

Data preprocessing and normalization can significantly smooth or reshape the landscape. While these transformations do not turn a fundamentally non-convex problem into a convex one, they can reduce pathological curvature or steep gradients in certain directions. Techniques that help include:

• Feature scaling: Ensuring each input feature is on a similar scale (e.g., standardization to zero mean and unit variance) so that gradient steps are balanced across parameters. • Batch normalization: Applied inside the network to stabilize distributions of layer inputs and outputs, which can reduce internal covariate shift. This does not guarantee convexity, but often empirically yields faster and more stable training. • Weight normalization or layer normalization: Similar effect in smoothing the training dynamics. • Spectral normalization: Controlling the Lipschitz constant of certain layers to help with generalization and gradient stability.

All these transformations might reduce the severity of local minima or limit the chaotic nature of the cost landscape, but the function remains non-convex in the strict sense. Nevertheless, these transformations can be the difference between successful training and getting stuck or diverging early on.

Does non-convexity always mean “hard to optimize,” or can some non-convex functions actually be easier in practice?

Non-convex typically implies that, in theory, we cannot guarantee finding a global optimum using local search methods alone. However, certain non-convex functions are still relatively easy to optimize in practice, especially in high dimensions. The presence of broad, gently sloping minima can mean that standard gradient descent with appropriate heuristics converges to a solution that is good enough.

Deep learning is the prominent example: even though the cost functions are highly non-convex, standard mini-batch gradient descent often finds solutions that generalize effectively. Sometimes the entire cost surface is described as having many local minima, but they often have similar values of the objective (or are connected by flat valleys). This phenomenon may be less about it being “convex-like” and more about the high-dimensional geometry allowing for many equally good (or near-good) solutions.

Conversely, there exist non-convex functions with many narrow minima that are extremely difficult to optimize. The difference is highly problem-dependent.

How do we handle non-convex situations where the number of parameters grows extremely large, such as in massive language models?

Scaling up to billions or trillions of parameters (as in large language models) presents unique challenges:

• Memory constraints: Storing gradients, parameters, and optimizer states is non-trivial, and advanced distributed training strategies become necessary. The non-convex nature still persists; it is just that we now have far more degrees of freedom.

• Gradient noise: Large batch sizes or distributed mini-batches can decrease the inherent noise in gradient estimates, sometimes making the optimization trajectory more deterministic. This can be a double-edged sword because it might lead to sharper minima or hamper the ability to escape poor local minima. Conversely, smaller batch sizes can reintroduce beneficial noise but slow throughput.

• Learning rate schedules: Carefully tuned schedules (e.g., warmup, cosine decay, or adaptive approaches) are crucial to ensure the model traverses the vast parameter space effectively. Non-convex landscapes in high dimension can have wide flat basins that are beneficial if the optimizer can find them.

• Architecture design: Techniques like skip connections, attention mechanisms, or residual blocks often help in large-scale models by alleviating vanishing gradients and stabilizing training. Though these do not confer convexity, they reduce pathological curvature and help the optimizer find good solutions more reliably.

Hence, while scaling up intensifies the non-convex challenge, it also provides more capacity for the model to capture complex patterns. Empirical evidence suggests that bigger, deeper models often find high-quality minima as long as the optimization strategy (initialization, learning rate schedule, etc.) is managed carefully.

Could evolutionary or population-based approaches circumvent some of the local minima issues in non-convex optimization?

Evolutionary algorithms, genetic algorithms, and population-based methods can in principle explore the parameter space more globally. They maintain a population of candidate solutions and apply selection, mutation, and crossover to generate new solutions. This might reduce the chance of getting stuck in one local minimum, as some individuals in the population might escape to other regions of the landscape.

However, these methods can be computationally expensive for large-scale neural network training. They typically require evaluating many candidate solutions each iteration, which is prohibitive if each candidate is a huge model with billions of parameters. Still, smaller or specialized problems may benefit from evolutionary approaches, and hybrid approaches (e.g., combining gradient-based methods with evolutionary search for hyperparameters) can be effective.

Even so, population-based methods do not guarantee they will find the global optimum in a highly non-convex space, but they can sometimes explore more broadly than purely local gradient descent methods. Balancing computation cost with exploration is the main challenge.

How do we distinguish between local minima and saddle points in a non-convex cost function, and why does it matter?

In a non-convex cost surface, a local minimum is a point where the gradient is zero and the Hessian is positive semidefinite in the relevant directions, whereas a saddle point is a stationary point where the Hessian has both positive and negative eigenvalues, so the curvature is not consistently “bowl-shaped.”

Distinguishing them matters because:

• Saddle points: The cost can be flat in many directions but also rise in others. Training can stall near saddle points because gradients become small, but the model is not truly at a basin of attraction. Sometimes small perturbations or noise can push the parameters away from a saddle point, resuming descent.

• Local minima: A genuine local minimum might be harder to escape without a significant shift. If the local minimum is suboptimal, the model might be stuck. But in high-dimensional spaces, many local minima end up having comparable loss values, so being stuck in a local minimum is not necessarily bad.

Empirical studies suggest that saddle points and flat plateaus can be more troublesome than truly bad local minima in very high-dimensional neural networks. Optimization techniques that incorporate momentum, noise, or adaptive steps can help overcome those stalls at saddle points. In many neural network architectures, local minima are often “good enough,” so the main worry is not so much that you find a local minimum, but that you get caught in a plateau or sharp region that hinders generalization.

Could certain initialization strategies inadvertently lead to suboptimal minima in a non-convex setting?

Initialization can heavily influence which region of the loss landscape the optimizer encounters first. Poorly chosen initial weights could:

• Immediately saturate certain non-linear activations (e.g., large negative biases with a sigmoid can saturate neurons at 0). • Induce exploding gradients if the scale of the initial weights is too large, causing updates to be chaotic early in training. • Bias the model to certain symmetrical or degenerate regions of the parameter space, especially if you initialize all weights identically or with no randomization.

Many specialized heuristics have been proposed for neural network initialization, such as Xavier (Glorot) initialization or He initialization, which aim to preserve variance in forward and backward passes. These heuristics do not make the cost function convex, but they reduce the likelihood of getting stuck in poor local minima or other pathological regions right from the beginning.

Moreover, layer-specific or task-specific initializations can be beneficial (e.g., pretraining certain layers on related tasks). This can “nudge” the model toward regions of the parameter space that are known to be good starting points, improving final performance despite the non-convex nature of the problem.

Are there special classes of non-convex problems that still have guaranteed convergence to global optima?

Yes, certain non-convex problems exhibit special structure that allows guaranteed convergence:

• Biconvex problems: The function is convex in each set of variables while holding the others fixed, but not jointly convex. While not guaranteed to be globally convergent in all cases, some specialized methods can find global solutions for certain biconvex formulations if additional constraints or properties are satisfied.

• Geodesically convex problems: In some manifold settings (e.g., matrix completion with low-rank constraints on a Riemannian manifold), the problem can be convex in the geodesic sense, even though it is not Euclidean convex. This yields strong theoretical convergence guarantees for certain specialized optimization algorithms.

• Neural tangent kernel (NTK) regime: For very wide neural networks, some theoretical results indicate that training can behave like a convex optimization in function space, although these results have strong assumptions on architecture width and certain data distributions.

In standard practice, though, typical deep neural network training is not proven to converge globally, but works well empirically. Structured non-convex problems with additional theoretical properties are more of a research area than a mainstream approach in large-scale production deep learning.

When training large ensembles or using multi-objective optimization, how does convexity or non-convexity play out?

In multi-objective optimization (e.g., optimizing both accuracy and fairness, or accuracy and latency), each objective might be convex or non-convex, and you often form a Pareto front of trade-offs rather than a single global optimum. Even if each individual objective is convex with respect to parameters, combining them can turn the problem non-convex or might still require searching for a set of solutions that represent different trade-offs.

In ensemble methods, each individual model’s training cost might be non-convex, so training them jointly (like in a multi-task or multi-loss setting) can compound the non-convexities. If you train each model separately and then ensemble, each model navigates its own non-convex cost function. The final combination can actually be somewhat smoothing, because it’s effectively an average of predictions, but this smoothing happens after each model’s training is done.

How do issues like gradient clipping or optimizer constraints interact with non-convex cost functions?

Gradient clipping is often used in deep learning to prevent exploding gradients, especially in RNNs or very deep networks. In a non-convex setting, clipping can help the optimizer avoid large, erratic updates that jump across distant regions of the loss surface. However, one must be cautious:

• Aggressive clipping might stall progress in narrow but steep descent directions. • Improper clipping thresholds can break the delicate balance of gradient magnitudes, causing the optimizer to behave unpredictably and potentially ignore beneficial directions.

Similarly, constraints on parameters or optimizers (e.g., L1 constraints, weight positivity constraints, or differential privacy constraints) can shape the feasible set in complicated ways. This shaping can sometimes reduce the effective dimensionality or restrict the parameter space to more “well-behaved” regions, but it does not guarantee convexity. Instead, it imposes geometry that might or might not help in practice. The interplay of constraints, clipping, and non-convex cost surfaces often needs extensive experimentation to find stable configurations.

What are common misconceptions about convexity and non-convexity in practical ML applications?

• Misconception: “Non-convex means random guessing.” In reality, gradient-based optimization can reliably find good regions in non-convex landscapes if the problem structure is favorable and enough data is available. • Misconception: “Convex models are always better for real-world data.” While convex models (like linear or logistic regression) have elegant guarantees, they may lack the capacity to model the complexities of high-dimensional real-world problems. Non-convex neural networks often outperform simpler convex models in tasks like image recognition, speech, and language. • Misconception: “Local minima are the only problem in non-convex optimization.” In fact, saddle points and plateaus can be even more problematic. • Misconception: “If you add a convex regularizer, you make the whole model convex.” As discussed, combining a convex regularizer with a non-convex model does not produce a convex overall objective. • Misconception: “There is a single best strategy to train non-convex models.” Optimization success often depends on architecture, initialization, learning rate scheduling, data properties, etc. It is a multi-factor problem requiring careful hyperparameter tuning and domain knowledge.

Do we need different validation or debugging strategies for non-convex models compared to convex ones?

You often need more rigorous checks with non-convex models because training can fail or plateau for reasons unrelated to data misfit. Recommended strategies include:

• Monitoring training and validation loss curves for signs of plateauing or divergence. • Trying multiple random initializations to see if the model consistently converges to similar performance or drastically different outcomes. • Performing ablations: remove or replace certain layers or regularizers to see if they cause the training to get stuck. • Checking gradient magnitudes and distributions across layers, ensuring no single layer saturates or sees vanishing/exploding gradients. • Varying learning rates or applying learning rate schedules to see if it overcomes local traps. • Using test tasks or smaller subsets of data to quickly iterate on hyperparameters before scaling up.

Convex models have simpler debugging pathways: if gradient descent diverges in a convex setting, it’s almost certainly due to too large a learning rate or data issues, because any local minimum is the global solution. Non-convex models can fail for many other subtle reasons, including architecture design, activation saturation, or mismatch between the data distribution and model capacity.

Could gradient-free methods help us circumvent non-convex local minima entirely?

Gradient-free methods, such as random search, Bayesian optimization, or derivative-free optimization, do not require explicit gradients and can sometimes explore the parameter space differently. However:

• For high-dimensional problems (like deep neural networks), gradient-free methods become extremely expensive. Evaluating large parameter sets with minimal guidance from gradients leads to combinatorial explosion in search space. • Bayesian optimization is popular for hyperparameter tuning but not typically for direct weight optimization in deep networks. • Derivative-free methods can be helpful if the objective function is discontinuous or not differentiable. But standard deep networks are differentiable (barring some activation corners), so gradient-based methods are typically more efficient and scalable.

Hence, while gradient-free approaches might theoretically be more global, they are rarely used for full-scale neural network training because of computational constraints. They may be used in smaller or special contexts.

Still, non-convex issues remain, since global methods do not guarantee they can systematically escape all bad local minima without incurring massive computational costs.

Is there any benefit to analyzing convex relaxations of a non-convex problem?

Yes, sometimes analyzing a convex relaxation or upper/lower bounds can provide insights:

• It can give a theoretical baseline or bound for the best achievable solution if the problem were convex. This can be helpful to understand how “far” your non-convex solution might be from a hypothetical global optimum. • In certain integer programming or combinatorial optimization problems, solving a convex relaxation (like linear or semidefinite programming relaxation) and then rounding can yield approximate solutions to the original non-convex problem.

For neural networks, convex relaxations (like the convex outer polytope of ReLU networks) are an active area of research in verification and robustness. These relaxations are too loose to solve the full training problem exactly, but they can help in bounding or verifying certain properties of the network (like adversarial robustness).

Hence, while you cannot train a standard deep network purely via a convex relaxation, the analysis might reveal theoretical properties or highlight where the network might be vulnerable.

Could dynamic, online, or streaming data scenarios exacerbate non-convex training issues?

Yes, when data arrives in a stream or changes over time, the model might need to continually adapt. This is often called online learning or continual learning. In a non-convex setting, new data distributions can:

• Shift the landscape dynamically, making previously found minima suboptimal. • Potentially interfere with older knowledge, leading to “catastrophic forgetting” in neural networks if care is not taken. • Require incremental updates without the benefit of re-initializing or re-shuffling a static dataset.

Approaches to handle these include storing a small replay buffer of past data, using regularization to preserve old parameters, or adopting meta-learning strategies. None of these methods eliminate the fundamental non-convexity, but they help the model navigate shifting cost landscapes over time. The complexities of real-world data distribution shifts can pose additional pitfalls that purely convex online learning methods (like linear regression with an online update rule) would handle more gracefully in theoretical terms, but at the cost of lower representational power.

What are the main real-world implications of using non-convex cost functions in high-stakes or mission-critical applications?

In high-stakes applications (e.g., medical diagnostics, autonomous driving, financial forecasting), using non-convex models means:

• Less interpretability: Non-convex models (especially deep nets) can be opaque. Uncertainty in local minima can hamper transparent decision-making or error analysis. • Dependence on heuristics: The final solution’s quality may heavily depend on tuning or random initialization. This raises questions of reproducibility and reliability. • Potential for surprising failure modes: If the model was trained in a suboptimal region of the cost space or on insufficient data, it might behave unpredictably in edge cases. • Regulatory or compliance challenges: Stakeholders might demand rigorous proof or explanation of decisions, which is more straightforward for convex or linear models where global optimality or simpler structures are guaranteed.

Nevertheless, these non-convex methods are widely used in these domains because of their superior performance on complex tasks. Often the solution is to add additional layers of validation, interpretability tools (e.g., feature attribution), robust test protocols, or real-time anomaly detection, rather than to revert to purely convex models that may not perform as well overall.