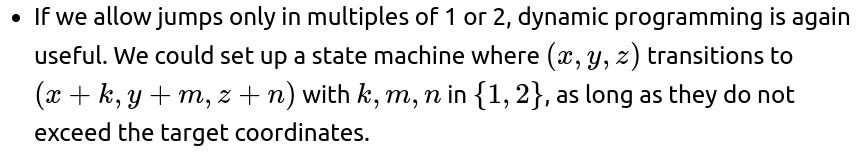ML Interview Q Series: Counting Distinct Paths in a 3D Grid Using Multinomial Coefficients
Browse all the Probability Interview Questions here.
Imagine you are located at the origin (0, 0, 0) in a three-dimensional space. You aim to get to (3, 3, 3) by making moves only in three directions: upward, rightward, or forward. How many distinct paths can you take?
Short Compact solution
To move from (0,0,0) to (3,3,3), you must make exactly three moves up, three moves right, and three moves forward, for a total of nine moves. The number of distinct ways to arrange these nine moves (where each move in the same direction is indistinguishable) is computed by the multinomial coefficient. Hence, the count of all distinct paths is:
Comprehensive Explanation
Each path consists of nine total moves, split evenly into three categories: three “up” moves, three “right” moves, and three “forward” moves. One way to see this is to imagine writing out a sequence of nine letters, where each letter can be “U” (up), “R” (right), or “F” (forward). Since you must use each letter exactly three times, the total number of distinct sequences is given by dividing the factorial of nine (the total length) by the factorial of three for each group:
This formula is a direct application of the multinomial coefficient. Essentially, 9! counts all permutations of nine positions, but since each of the three positions of “U” are identical among themselves (and similarly for “R” and “F”), we must divide by 3! for each repeated direction.
Here is a concise Python snippet to verify the result using a straightforward combinatorial function:
from math import factorial
numerator = factorial(9)
denominator = factorial(3)*factorial(3)*factorial(3)
paths = numerator // denominator
print(paths) # Outputs 1680
Follow-up question: How would you generalize this result for moving from (0,0,0) to (a,b,c)?
If we generalize the destination to be (a, b, c), then the total number of steps needed is a + b + c. Among these a + b + c moves, exactly a must be in one direction (say “up”), b in another direction (say “right”), and c in the third direction (say “forward”). The total number of unique paths is:
In a Python code snippet, we can write:
from math import factorial
def count_paths(a, b, c):
return factorial(a + b + c) // (factorial(a) * factorial(b) * factorial(c))
print(count_paths(3,3,3)) # 1680
Follow-up question: How could you confirm this by a more exhaustive or algorithmic approach?
A simple Depth-First Search (DFS) or Breadth-First Search (BFS) in a grid-like structure can be used. You can treat each coordinate (x,y,z) as a node and move only in the three allowable directions. A BFS approach, while more computationally expensive than the direct combinatorial formula for larger numbers, would confirm the count for relatively small targets like (3,3,3).
Below is an example BFS in Python for small grid sizes:
from collections import deque
def bfs_count_paths_3d(a, b, c):
queue = deque()
queue.append((0,0,0))
visited_paths = {(0,0,0): 1} # Dictionary storing how many ways to get to each point
while queue:
x, y, z = queue.popleft()
for dx, dy, dz in [(1,0,0), (0,1,0), (0,0,1)]:
nx, ny, nz = x+dx, y+dy, z+dz
# Check bounds
if nx <= a and ny <= b and nz <= c:
if (nx,ny,nz) not in visited_paths:
visited_paths[(nx,ny,nz)] = 0
queue.append((nx,ny,nz))
visited_paths[(nx,ny,nz)] += visited_paths[(x,y,z)]
return visited_paths.get((a,b,c), 0)
print(bfs_count_paths_3d(3,3,3)) # 1680
Internally, this code initializes a queue and maintains a record of how many ways lead to each coordinate. For each point, we expand in the allowed directions. Over time, the number of ways to reach (3,3,3) accumulates. While this method is more brute-force, it is instructive and provides a sanity check.
Follow-up question: What if negative moves were allowed as well?
If negative moves are allowed, then the problem becomes much more complex since you can move in multiple directions (potentially returning to previous coordinates). Simply counting from (0,0,0) to (3,3,3) without restricting the total path length can lead to infinitely many routes unless you impose a limit on the number of moves.
One typical scenario is to set a maximum number of moves. In that case, you would need to count all possible sequences within that move budget that land exactly on (3,3,3). You would usually employ dynamic programming to handle the possibility of reversing direction and re-visiting coordinates.
Follow-up question: Why is this type of counting relevant in machine learning or data science?
Although it might look like a straightforward combinatorial puzzle, path-counting problems show up in various contexts such as dynamic programming algorithms, lattice-based probability models (e.g., random walks), and some Markov chain analyses where transitions only move in certain directions. Understanding how to count the number of ways to reach certain states is fundamental in computing probabilities of events in state-space models or in enumerating discrete paths in model architectures (e.g., certain neural network structures or Bayesian network structures).
Moreover, combinatorial reasoning is essential in analyzing the complexity of algorithms and in parsing high-dimensional data transitions in certain advanced topics such as reinforcement learning, where the number of possible state-action sequences can explode combinatorially.
Follow-up question: Are there pitfalls in practical implementations?
One major pitfall is dealing with large factorials when a, b, and c become large. Factorials grow extremely fast, leading to integer overflow in languages that do not support big integers by default. In Python, integer overflow is not an issue because Python’s int can expand as needed, but time to compute massive factorials may still become a performance concern. A typical way to handle large values is to use logarithms or precomputed factorial tables with modular arithmetic if only remainders are required.
Another subtlety involves ensuring the moves are properly constrained or that the boundaries of the grid are well-defined if you use an algorithmic approach. In BFS/DFS solutions, failure to handle boundary checks could incorrectly allow paths that go out of scope or double-count states.
Below are additional follow-up questions
What if we introduce a forbidden region in the 3D grid?
If certain points in the 3D grid are off-limits (an obstacle or forbidden region), then not every path that uses three “up,” three “right,” and three “forward” moves remains valid. We can no longer use a direct combinatorial formula because it counts all paths without considering obstructions. Instead, we might:
Use dynamic programming:
Use a BFS/DFS approach that skips forbidden nodes, similar to the BFS code described earlier, but ignore any move that tries to enter a forbidden coordinate.
Potential pitfalls and edge cases:
Marking forbidden cells incorrectly can lead to double-counting or ignoring valid routes.
If the origin or the destination is blocked, the path count is trivially zero.
Dynamic programming array or BFS memory usage can blow up if the grid is large and you store data for every coordinate.
What if the step sizes are not restricted to exactly 1 in each direction?
If you are allowed to move in increments greater than 1 for some steps (for example, you can jump two steps upward in one move), the counting changes significantly. Instead of each “up” move being identical, you would have different categories like “move up by 1,” “move up by 2,” etc. The solution might then be approached by:
Breaking the problem into partitions: We must find all integer partitions of the total distance that sum up to 3 in each dimension if 3 is still the target. Each distinct partition in each dimension multiplies out with the partitions for the other dimensions to form the total path count.
Potential pitfalls and edge cases:
Keeping track of which jump sizes are allowed can become complicated if the set of allowed steps is large.
Some combinations of step sizes may skip over points, complicating the question of how to define “distinct paths.” If you jump from z=0 to z=2 in one move, do we consider that the same or different from taking two forward moves of z=1 each?
How do we handle paths if the moves can occur in any continuous order within each dimension (i.e., real-valued step increments) but still sum to (3,3,3)?
When moves are no longer discrete, you transition into a continuous space problem, which is fundamentally different. In that scenario, “number of distinct paths” may no longer be a meaningful question in simple combinatorial terms; we might talk about path integrals in a continuous domain.
One approach is to interpret the problem as counting distinct sequences of continuous increments summing to 3 in each of the three dimensions, which can be infinite in quantity under typical definitions.
You would need constraints, such as bounding the number of sub-steps or restricting increments to rational fractions, to keep the set countable.
Potential pitfalls and edge cases:
In continuous problems, the notion of distinct paths might require a geometric or measure-theoretic perspective (e.g., comparing path lengths, using integrals to quantify volumes in function space).
Without additional constraints, you end up with uncountably infinite solutions.
What if each dimension has a different final coordinate, and you only have partial knowledge of one dimension’s final count?
Imagine you know the number of ways to go from (0,0) to (a,b) in 2D, but you still need to factor in the third dimension. If (a,b) is known to have X ways, how does that help for (a,b,c) in 3D?
Potential pitfalls and edge cases:
Double-counting if you merge the 2D and 3D sequences incorrectly, or if the 2D path is not valid in the 3D sense (for instance, obstacles in the 3D dimension that do not appear in the 2D slice).
Failing to track partial constraints (e.g., if the 2D path has some region blocked that doesn’t appear blocked in the 3D version).
How would you handle a scenario where the allowable directions rotate as you move?
Sometimes, problems involve a set of directions that change based on your current coordinate or orientation, rather than always being “up,” “right,” or “forward.” If you are dealing with a rotating frame of reference or direction constraints that differ at each step:
You might set up a graph where each node is a combination of position and orientation. For instance, (x,y,z,orientation) could define a unique node.
Edges in the graph represent valid moves in the direction permitted by that orientation. You would then run a path-counting algorithm (such as dynamic programming or BFS in the higher-dimensional state space) to find the number of ways to reach (3,3,3,some valid orientation).
Potential pitfalls and edge cases:
The state space grows because orientation adds extra dimensions. This can cause exponential explosions in complexity for large problems.
Ensuring consistency between consecutive steps is tricky. If each orientation only allows certain transitions, you must carefully encode the adjacency rules.
What if you need not just the number of paths but the probability of choosing one path at random (given some distribution of moves)?