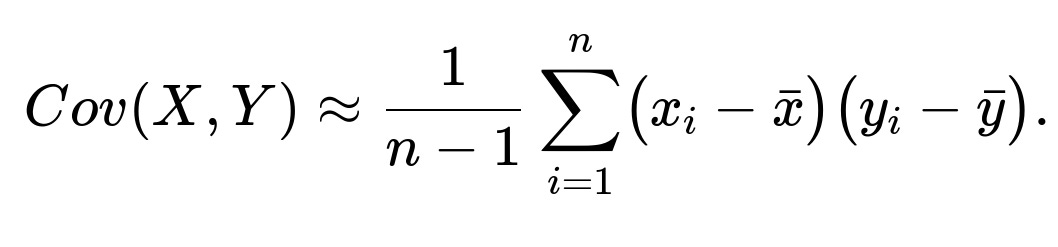ML Interview Q Series: Covariance and Correlation: Definitions, Formulas, Differences, and Applications Explained.
Browse all the Probability Interview Questions here.
Explain how to define covariance and correlation through their respective formulas, and highlight their differences and similarities
Short Compact solution
Covariance between two random variables X and Y is a linear measure of their relationship. Formally, it can be expressed as
This quantity can vary from negative infinity to positive infinity, and it reflects not only the direction of the relationship but also depends on the units of X and Y.
Correlation is obtained by normalizing the covariance by the standard deviations of X and Y, leading to a dimensionless measure:
It always lies within the range -1 to 1 and indicates the strength as well as direction of the linear relationship, independent of the underlying units of each variable.
Comprehensive Explanation
Covariance and correlation are both key statistical tools for measuring linear association between two variables. They capture how one variable changes with respect to another, but they do so in slightly different ways.
Understanding Covariance
Covariance reveals whether two variables move in the same direction or opposite directions on average. A positive covariance implies that as one variable increases, the other also tends to increase, while a negative covariance means that as one variable increases, the other tends to decrease.
The magnitude of covariance depends on the scales of the variables involved. If X and Y have large numerical ranges, their covariance can be large in absolute value, and vice versa. Consequently, interpreting a raw covariance value can sometimes be tricky because it may be driven by the variables’ units rather than purely by the strength of the linear relationship.
Understanding Correlation
Correlation addresses the scaling issue by dividing out the standard deviations of X and Y. This produces a unitless value that always lies in the interval [-1, 1]. A value closer to +1 indicates a strong positive linear relationship, -1 indicates a strong negative linear relationship, and values near 0 suggest no strong linear pattern (although non-linear relationships may still exist).
Because correlation is standardized, it is often preferred for comparing relationships across different pairs of variables whose scales might differ significantly. However, it is important to note that correlation only captures linear relationships. Non-linear associations will not be well-represented by correlation alone.
Key Differences
Both covariance and correlation measure linear dependence. However:
Covariance can be any real number from negative infinity to positive infinity; correlation is always constrained to the range [-1, 1].
Covariance retains the units of the variables (e.g., meters squared if one variable is in meters and the other in meters); correlation is dimensionless.
Correlation is a rescaled version of covariance that factors in the individual variability (i.e., standard deviations) of the two variables.
Mathematical Illustration
If you have a dataset of sample pairs
the sample covariance can be computed as an average of the products of deviations from the mean:
The corresponding sample correlation is then
These formulas are typically used in practical data analysis to compute empirical covariance and correlation from collected data.
Practical Example in Python
Below is a simple Python code snippet demonstrating how one might compute covariance and correlation for a pair of numpy arrays:
import numpy as np
# Example data
X = np.array([1.0, 2.5, 3.7, 4.1])
Y = np.array([2.0, 2.8, 3.9, 5.0])
# Calculate means
mean_X = np.mean(X)
mean_Y = np.mean(Y)
# Compute sample covariance manually
cov_manual = np.sum((X - mean_X) * (Y - mean_Y)) / (len(X) - 1)
# Compute sample correlation manually
corr_manual = cov_manual / (np.std(X, ddof=1) * np.std(Y, ddof=1))
# Compare with NumPy's built-in functions
cov_np = np.cov(X, Y, ddof=1)[0, 1] # Covariance
corr_np = np.corrcoef(X, Y)[0, 1] # Correlation
print("Manual Covariance:", cov_manual)
print("Manual Correlation:", corr_manual)
print("NumPy Covariance:", cov_np)
print("NumPy Correlation:", corr_np)
In this code:
np.cov(X, Y, ddof=1)returns the sample covariance matrix with X as row 0 and Y as row 1.np.corrcoef(X, Y)returns the correlation matrix, with the correlation in the off-diagonal entries.
Use in Machine Learning
In machine learning and data science, understanding covariance and correlation is crucial for tasks such as:
Feature selection: Highly correlated features may provide redundant information.
Exploratory data analysis: Correlation matrices are common in analyzing pairwise relationships among features.
Dimensionality reduction: Techniques like Principal Component Analysis (PCA) rely on the covariance matrix.
Correlation coefficients are especially common in data preprocessing and feature engineering, since they help identify which input variables might be most predictive or redundant for a target variable.
Follow-up question: How do we interpret a correlation coefficient that is close to zero if the underlying relationship is non-linear?
Even if the correlation coefficient is near zero, the two variables might still be strongly related in a non-linear way. For instance, if Y = X² (a perfect parabola around the origin), the Pearson correlation might be close to zero, yet there is a clear pattern in the data. In real-world scenarios, always visualize data or use additional methods (like rank-based correlation measures—Spearman or Kendall—if you suspect monotonic non-linear trends) to ensure that a near-zero correlation does not hide a non-linear relationship.
Follow-up question: When would you choose covariance over correlation?
Covariance might be more appropriate when the actual scale of changes in the variables is of direct interest. For example, in a financial portfolio analysis, one might care about the actual dollar variability among assets (covariances) rather than merely the normalized correlation. In most other scenarios, correlation tends to be more interpretable because it removes the effect of differing units.
Follow-up question: How do outliers affect correlation and covariance?
Outliers can significantly skew both covariance and correlation if they deviate strongly from the general linear pattern in the data. Since both measures rely on mean and variance concepts, any extreme data points can inflate or deflate the result disproportionately. It is often advisable to analyze data distribution, remove or down-weight outliers (if justified), or employ robust correlation measures that are less influenced by outliers.
Follow-up question: Can correlation imply causation?
Correlation does not imply causation. A high correlation might mean that two variables move together in a consistent fashion, but there might be hidden confounding factors. Determining causation typically requires controlled experiments, domain expertise, or more sophisticated approaches such as causal inference frameworks.
Follow-up question: How do you handle missing values when computing correlation in practice?
In practical data science workflows, one can drop rows with missing data if the quantity of missing values is small. Alternatively, various imputation strategies can be used (e.g., mean imputation, regression-based imputation, or more advanced methods like multiple imputation) to retain as many observations as possible. The choice depends on the dataset size, the pattern of missingness (random or systematic), and the potential bias introduced by different imputation approaches.
Follow-up question: Is there a scenario where correlation = 1 but the relationship is not strictly linear?
If the correlation is strictly 1 or -1 using Pearson's correlation, it implies a perfect linear fit among the data points. However, be mindful of numerical precision issues. In practice, a correlation extremely close to 1 can still be off from exact linearity due to floating-point roundoff. But theoretically, a correlation of 1 indicates the points lie exactly on a line with positive slope, and a correlation of -1 indicates they lie perfectly on a line with negative slope.
Follow-up question: How is correlation used in feature selection?
In feature selection, high correlation between two features might signal redundancy. If two features convey essentially the same information, one of them might be excluded to reduce model complexity and overfitting risk. Additionally, correlation between a feature and the target variable can be an initial heuristic to gauge potential predictive power. However, it is not the sole metric for selecting features, as non-linear relationships and complex interactions might not be captured by linear correlation alone.
Below are additional follow-up questions
How does correlation differ from rank-based correlation measures like Spearman’s correlation or Kendall’s tau, and when should these be used?
Spearman’s correlation and Kendall’s tau are both rank-based (non-parametric) measures that evaluate the monotonic relationship between two variables. In contrast, Pearson’s correlation measures linear relationships. When data exhibit outliers, heavy tails, or clear monotonic (but potentially non-linear) trends, Spearman or Kendall often provide a more robust and interpretable measure because they rely on the relative ordering of data points rather than the raw distance from the mean.
A potential pitfall arises if the data are strictly linear but heavily influenced by noise. In such a scenario, Spearman’s correlation might understate the true linear trend because it ignores the raw distances in favor of ranks. Conversely, if the data have outliers that distort means and standard deviations, Pearson’s correlation might be misleading, whereas rank-based methods are more resistant to outliers. Another subtle issue appears if the dataset contains many tied values; Spearman’s correlation can still be computed, but Kendall’s tau is sometimes considered more robust in the presence of ties, although it is more computationally intensive.
How might collinearity among multiple variables affect correlation analysis in multivariate contexts, and how can it be detected or mitigated?
Collinearity occurs when two or more variables in a dataset are highly correlated, making it hard to distinguish their individual effects. In a regression context, this leads to inflated variance in the estimated coefficients, weakening statistical tests and interpretability.
A standard detection method is to compute a correlation matrix and look for large absolute correlations (e.g., above 0.8) or use Variance Inflation Factors (VIF) for each predictor. Multicollinearity can also hide in the data if several variables share smaller pairwise correlations but collectively exhibit high dependence. Techniques such as Principal Component Analysis (PCA) can help mitigate collinearity by transforming features into orthogonal components, but the interpretation of original variables might become less direct. Another approach is regularization (like Ridge or Lasso regression) that down-weights or shrinks correlated coefficients, reducing variance at the cost of possibly biasing the estimates.
A subtle pitfall is overlooking combinations of multiple variables that do not appear highly correlated pairwise yet combine to produce near-singular covariance matrices. Hence, simply checking pairwise correlation might not be enough. Checking determinant or eigenvalues of the covariance matrix, or employing specialized diagnostics, can reveal more complex dependencies.
In high-dimensional datasets, how do we effectively compute and interpret a large correlation matrix, and what pitfalls should we watch out for?
When the number of features is very large (hundreds or thousands), computing and storing a full correlation matrix can be resource-intensive. Even after calculation, interpreting such a large matrix is challenging because it’s difficult to glean meaningful insights from so many pairwise relationships.
One strategy is to use dimensionality reduction or feature selection first. Approaches like PCA can help identify sets of features that explain most variance. Another approach is to visualize the correlation matrix using heatmaps with clustering (e.g., hierarchical clustering to group highly correlated variables). Still, a major pitfall is multiple comparisons: with thousands of correlations, many may appear statistically significant by chance alone. Controlling the False Discovery Rate (FDR) or using other multiple-comparison corrections can reduce false positives.
An additional subtlety arises if the data matrix has more features than observations (the so-called “p >> n” problem). Traditional estimates of correlation can be extremely noisy in such scenarios. Techniques like shrinkage estimates of the covariance or correlation matrix can help stabilize estimates when the dataset is high-dimensional.
Why do parametric tests often rely on Pearson’s correlation, while non-parametric tests might opt for rank-based correlations? Are there any boundary scenarios?
Parametric tests that assume normally distributed data rely on Pearson’s correlation, as it directly links the covariance of two normally distributed variables to their linear association. If these assumptions hold—particularly linearity and normality—Pearson’s correlation efficiently captures the strength and significance of the relationship.
Non-parametric tests, on the other hand, do not require normality assumptions. Instead, they rely on the ordering of data (ranks) and detect monotonic patterns. In scenarios where the data are heavily skewed, have outliers, or follow unknown distributions, Spearman’s or Kendall’s correlation gives more reliable or interpretable findings.
A boundary scenario occurs if the data come from a highly non-normal distribution that is still linearly related (e.g., large outliers but a strong linear pattern). Pearson’s correlation might become unreliable as the extreme points dominate the mean and variance. In such cases, using rank-based correlation may dampen the effect of outliers, but it may also lose sensitivity to finer linear details in the bulk of the data. A thorough approach often involves using diagnostic plots and testing normality assumptions to decide which correlation measure is most appropriate.
Are correlation and covariance always symmetrical, and how does this symmetry affect covariance or correlation matrices?
Yes, both covariance and correlation are inherently symmetrical in the sense that
This arises because the formula for covariance involves multiplying deviations in X and Y, which is inherently commutative. Consequently, both the covariance matrix and correlation matrix are symmetric matrices: the off-diagonal elements above the diagonal mirror those below the diagonal.
This symmetry implies that covariance and correlation matrices can be analyzed using linear algebra techniques that exploit symmetry. For example, these matrices are guaranteed to be positive semi-definite (they can be shown to have non-negative eigenvalues in theory, assuming no numerical issues). That property is crucial in multivariate statistics (e.g., in computing the Mahalanobis distance or performing PCA). One edge case is if the data contain linear dependencies or near-dependencies, which may lead to singular (or nearly singular) covariance matrices with zero or near-zero eigenvalues, creating computational and interpretive difficulties.
In practice, how do advanced measures like distance correlation differ from Pearson’s correlation, and when might distance correlation be more appropriate?
Distance correlation is a measure that goes beyond linear or even strictly monotonic relationships. It captures any form of dependence between two variables, whether linear or non-linear, by comparing pairwise distances within each variable’s distribution. If variables are independent in a broad sense, the distance correlation is zero, whereas a Pearson correlation of zero only indicates a lack of linear dependence.
A key advantage is that distance correlation can detect relationships like quadratic or sinusoidal patterns. However, a pitfall is interpretability: a non-zero distance correlation indicates dependence, but it does not specify how or why the relationship manifests (linear, polynomial, etc.). It also can be more computationally expensive for large datasets and might be less intuitive to interpret for domain experts used to linear correlation. Another subtlety is that in high-dimensional settings, even distance correlation might become unstable or difficult to interpret if not carefully controlled or regularized.
Can correlation be misleading in cyclical or time-series data that contain trends or seasonality?
Yes. In time-series data, two variables might exhibit high correlation simply because they both share an upward trend over time rather than being causally or meaningfully related. Similarly, cyclical patterns (like seasonal peaks and troughs) can create misleadingly strong correlations if variables share the same seasonality.
A typical mitigation approach is to remove trends or seasonality from the data, for example by differencing or applying seasonal decomposition. One can then compute correlation on the residuals or the differenced data, which can better isolate genuine relationships from coincidental alignment in trend or cyclical patterns. A hidden pitfall is over-differencing, which could eliminate meaningful long-term relationships or overshadow real patterns. Also, ignoring the autocorrelation within each time series can mask or distort correlation estimates.
If we apply transformations (such as log, power, or Box-Cox) to data, how might this affect covariance and correlation?
Transformations can drastically change the distribution shape and variance of a dataset, often making relationships more linear. For instance, a log transform may convert multiplicative relationships into additive ones, revealing a more stable linear correlation that is not apparent in raw data. Because correlation is scale-invariant, a transformation that stabilizes variance and normalizes the data can lead to a more reliable Pearson’s correlation.
However, a pitfall is applying transformations arbitrarily and drawing spurious conclusions. For example, if the transformation is chosen simply to maximize correlation, it can bias results and produce overfitted findings that do not generalize. Another edge case is negative or zero values in the data, which complicates or precludes the use of certain transformations (like the log transform). Ensuring consistency (and invertibility if needed) is crucial for interpretability when using transformed variables in downstream analyses.
How does heteroskedasticity impact correlation, and is there a correlation measure that accounts for it?
Heteroskedasticity occurs when the variability of one variable changes systematically with the level of another variable. In such contexts, the assumptions behind ordinary linear models—specifically that errors have constant variance—are violated, and Pearson’s correlation might be misleading because the variance of the residuals is not uniform across all ranges of X.
While there is no universal “heteroskedasticity-adjusted correlation,” methods like weighted least squares can down-weight observations that exhibit disproportionately large variance. Rank-based correlations are sometimes more stable under heteroskedasticity, though they do not specifically account for the changing variance—rather, they simply consider ranks. A real-world example is income data, where variability (standard deviation) grows at higher income levels. A naive correlation analysis could be overly influenced by the wide spread at high incomes and may not reflect lower-income data well. Analysts should examine residual plots or use tests for heteroskedasticity (like Breusch-Pagan) to detect the issue before interpreting simple correlation metrics.
In factor analysis or PCA, how do we decide whether to use a covariance matrix or a correlation matrix, and what are the consequences of each choice?
In Principal Component Analysis (PCA) or factor analysis, using the covariance matrix preserves the original scale of the variables, which can be important if absolute variability matters (e.g., in finance, a larger variance in returns might be key to risk assessment). However, variables with larger scales dominate the first principal components more strongly because they have larger variances.
Using the correlation matrix, on the other hand, standardizes each variable to unit variance before extracting principal components. This ensures that all variables contribute equally, regardless of their raw scale. This approach is appropriate when the measurement units are arbitrary or when no single variable’s scale should dominate the analysis. The pitfall is that truly meaningful scale differences could be lost if standardization is performed without domain-specific justification. Another subtlety arises if certain variables inherently exhibit very small or very large variances (e.g., counts vs. continuous measurements). Normalizing them indiscriminately might distort the interpretation of the resulting factors or principal components.