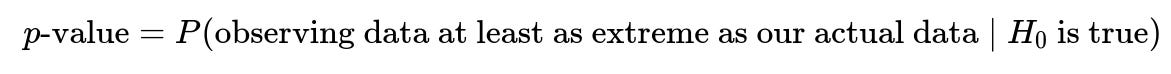ML Interview Q Series: Decoding P-values: Accurate Interpretation in Hypothesis Testing and A/B Experiments.
📚 Browse the full ML Interview series here.
Interpreting p-values: In the context of hypothesis testing (such as evaluating an A/B test for an ML model), what does a p-value represent? If an experiment yields a p-value of 0.01, what does that imply about the result, and what are common misconceptions about what a p-value means?
Meaning of the p-value
A p-value is associated with the framework of hypothesis testing. It is the probability of obtaining results at least as extreme as those observed, assuming the null hypothesis is true. When we conduct a hypothesis test (for example, evaluating whether there is a statistically significant improvement in an A/B test), we start with a null hypothesis, often denoted as (H_0). The null hypothesis typically states that there is "no difference" or "no effect" between two conditions (e.g., no difference in click-through rates between the control and treatment variants).
This expression means: If (H_0) truly holds, we look at how likely we would be to see the current data we actually observed (or something even more extreme in the same direction). A "small" p-value suggests that we would rarely observe such data if (H_0) was indeed correct.
Interpretation of a p-value of 0.01
A p-value of 0.01 typically signals that, assuming the null hypothesis is true, there is a 1% probability of observing data as extreme (or more extreme) than what you observed in your experiment. This is usually taken to mean that the evidence in the data is relatively strong against the null hypothesis, because such results would only occur 1% of the time by random chance if there really were no difference.
Many organizations use a conventional threshold, such as 0.05, to define "statistical significance." When the p-value is below that threshold (p < 0.05), the result is often called "statistically significant." For a p-value of 0.01, it is below 0.05, so the result would be considered statistically significant. However, choosing 0.05 or 0.01 as a cutoff is a somewhat arbitrary convention; it does not always imply real-world importance or guaranteed correctness.
Common misconceptions
One misconception is believing that the p-value is the probability that the null hypothesis is true. It does not represent (P(H_0 \mid \text{data})). Instead, it represents (P(\text{data} \mid H_0)). They are fundamentally different quantities. Another common misconception is that a p-value tells you the probability that your result will replicate, or that there is a certain percentage chance the observed difference is "real." Neither is correct.
A further misconception is thinking that a small p-value automatically translates to a large real-world effect size. Even if a p-value is small, the actual magnitude of the difference in an A/B test might be negligible. Statistical significance does not necessarily equate to practical significance.
A related misconception is the notion that a p-value of 0.01 means there is a 1% chance the experiment’s findings are due to random chance. That is not strictly correct, because the p-value is computed under the assumption that chance is the only factor at work (i.e., the null hypothesis). It is not the probability that chance alone created your effect. It is the probability that if the null were true, you would see data as extreme or more extreme 1% of the time.
What are Type I and Type II errors, and how do they relate to p-values?
Type I error is rejecting the null hypothesis when the null hypothesis is actually true. In an A/B testing setting, this would mean concluding that your new model or variant is better when in reality it is not. The significance level ((\alpha)) of a test (often set at 0.05) is the maximum allowable probability of a Type I error. If you decide on an (\alpha) of 0.05, you are stating that you accept a 5% chance of erroneously rejecting a true null hypothesis.
The p-value is compared to (\alpha) to determine whether you should reject (H_0). When p-value < (\alpha), the result is said to be statistically significant, and you proceed to reject (H_0). The probability of incorrectly rejecting (H_0) (when (H_0) is in fact true) is tied to your chosen significance level, so if you set (\alpha = 0.05), you are accepting up to a 5% risk of a Type I error.
Type II error is failing to reject the null hypothesis when it is actually false. This relates to test power: the higher the power of your experiment design, the lower the chance of a Type II error. Power is defined as (1 - \beta), where (\beta) is the probability of making a Type II error. The p-value doesn’t directly measure power, but a well-chosen sample size can help ensure that your test has sufficient power to detect the effects that you care about.
What if we run multiple tests without accounting for multiple comparisons?
Conducting multiple hypothesis tests without any correction can inflate your overall Type I error rate. If you run many parallel tests and keep (\alpha = 0.05) for each test, the chance that you get at least one false positive (Type I error) across all tests increases substantially. Common ways to adjust for multiple comparisons include the Bonferroni correction, the Holm-Bonferroni method, or the Benjamini-Hochberg procedure. These methods adjust the threshold or procedure for declaring significance so that the overall family-wise error rate remains controlled at a desired level.
If you do not account for multiple comparisons, a p-value of 0.01 might be less meaningful than you think, because if you have 100 comparisons, purely by chance you might expect around 1 significant result at the 1% level even if all null hypotheses are truly correct. This can lead to “false discoveries” if the analyst is not careful.
How is the p-value connected to confidence intervals?
A 95% confidence interval for a parameter (for example, the difference in conversion rates between two variants) is closely related to a significance test at (\alpha = 0.05). A 95% confidence interval that does not include 0 is akin to rejecting the null hypothesis at that level. While a confidence interval provides a range of plausible values for the parameter, a p-value indicates how likely it is to see data at least as extreme, assuming no true effect. Both forms give related but distinct insights into the data. Confidence intervals help you see the potential size and direction of the effect, while p-values give a sense of how unexpected your results are under (H_0).
How do we avoid p-hacking and misinterpretation of p-values?
P-hacking arises when researchers run many analyses, measure many outcomes, or repeatedly peek at the data until they find a p-value below 0.05. This leads to overstated significance and false discoveries. Best practices include:
Using a clear hypothesis and analysis plan prior to collecting data. Correcting for multiple comparisons if you test multiple hypotheses. Performing power analysis to choose an adequate sample size. Reporting effect sizes and confidence intervals, not just p-values. Looking at real-world significance or cost-benefit considerations rather than only statistical significance.
Ensuring code and data transparency also helps. Colleagues or reviewers can validate whether the analyses conformed to a pre-established plan. In real-world ML product experiments, it is wise to avoid repeated significance testing as data trickles in, unless your procedure is specifically designed for sequential analysis (e.g., using group sequential methods or Bayesian approaches).
By carefully designing experiments, choosing an appropriate (\alpha), and interpreting results in the context of effect size, domain knowledge, and the cost of errors, one can get the most out of p-values and avoid the pitfalls and misconceptions tied to them.
Below are additional follow-up questions
What if the underlying assumptions of the statistical test are violated?
When we talk about p-values in a classical frequentist framework (for example, a t-test or a z-test), there are standard assumptions such as normality of residuals, independence of observations, and homoscedasticity (equal variances in different groups). If these assumptions are violated, the theoretical distributions used to compute the p-value (e.g., the t-distribution for a two-sample t-test) may not match the actual behavior of the data. Consequently, the calculated p-values might be misleading or incorrect.
One subtlety is that many tests (especially the t-test) are reasonably robust to mild violations of normality if sample sizes are sufficiently large, thanks to the Central Limit Theorem. However, if the dataset is small or has strong outliers, normality assumptions can be severely violated. In such cases:
You might switch to a non-parametric alternative (like the Mann-Whitney U test or Wilcoxon Signed-Rank test).
You might transform your data (log transform, Box-Cox transform, etc.) to stabilize variance or approximate normality.
You might use a permutation test or bootstrap-based test that does not rely on the same parametric assumptions.
An edge case is strong autocorrelation in time series data or in certain ML applications where the data points might not be truly independent. Even if sample sizes are large, correlated observations can cause standard tests to underestimate or overestimate variability, leading to incorrect p-values. For instance, if your data come from a streaming service with user sessions that overlap, independence assumptions might break down. In such scenarios, methods that model correlation (like mixed-effects models or time-series-specific tests) can help produce more reliable inferences.
How do small or large sample sizes affect the p-value interpretation?
Very small sample sizes
If your sample size is tiny, you might get unstable estimates of the variance or effect size. P-values in that context can swing dramatically with the addition or removal of just a few data points. Even if the effect is truly present, the test may not detect it due to low statistical power, resulting in a high likelihood of Type II error (failing to reject the null when it is indeed false). It also becomes more likely that assumptions of the test are not met (e.g., normality). Confidence intervals tend to be very wide, suggesting high uncertainty.
Very large sample sizes
With massive datasets, even minuscule differences can become “statistically significant” if the test’s assumptions are not violated. A difference that is practically irrelevant—for instance, a 0.0001% increase in a click-through rate—might yield a very low p-value simply because the sample size is enormous. In such scenarios, you may declare "statistically significant" but find the real-world impact is negligible. Here, it’s essential to look at effect sizes, confidence intervals, domain context, and cost-benefit analyses. Statistical significance alone does not imply practical significance.
A subtle pitfall in large-scale ML experiments is data leakage or unaccounted-for confounding factors. Because of the large volume of data, extremely small confounding effects can become detectable. You need careful experiment design (randomization, stratification if needed) to ensure that your measured effect is truly attributed to the condition being tested.
How do p-values differ for one-sided vs. two-sided tests, and when should each be used?
In hypothesis testing, you must define whether you’re testing a one-sided or two-sided alternative hypothesis:
One-sided test: You hypothesize a difference in a specific direction. For example, you might state that version B has a higher average conversion rate than version A. The entire significance “tail” is placed on one side of the distribution (above or below, depending on your direction).
Two-sided test: You hypothesize a difference in either direction. For instance, you only know that version B’s conversion rate might differ (be higher or lower) from version A’s, and you’re testing for any departure from the status quo.
If you use a one-sided test incorrectly (simply because you noticed your difference was positive and you only want to see significance in that direction), you can overstate the significance of your result. Realistically, a two-sided test is safer when you are open to the possibility of your new variant performing either better or worse. A one-sided test should be chosen before examining the data and only if a negative direction is of no practical or theoretical interest.
A common pitfall is to run a two-sided test, see a near-significant result in the expected direction, then switch to a one-sided test after seeing the data. This post-hoc decision effectively changes the experiment plan, increasing the risk of Type I error.
In what ways can correlated data or repeated measures impact p-value calculation?
In many real-world ML applications (especially in recommendation systems, time series forecasting, or repeated user testing scenarios), the assumption of independent and identically distributed samples can break. Correlation or repeated measures (e.g., the same user appearing multiple times under different conditions) can severely affect the estimated variance, typically making naive standard errors too low and p-values artificially small.
For example, if the same user is exposed to both control and treatment under a within-subject design, or if you measure the same user over multiple time points, repeated measurements are not truly independent. Handling these cases can involve:
Mixed-effects models (also known as hierarchical linear models): These introduce random intercepts/slopes for individuals or groups, helping capture correlation within the same user or group of users.
Blocking or stratification: If you know data come in blocks (for instance, days, geographies, or user cohorts), you can incorporate that in the modeling.
Time-series methods: If measurements are sequential, specialized time-series analysis (ARIMA, state-space models, etc.) can factor in autocorrelation.
Failing to address correlation often makes p-values misleadingly small, because the tests assume more independent information is present than there really is.
How do we handle missing data in hypothesis testing, and how does it affect p-values?
Missing data often arises in A/B tests or observational studies. For example, some users might not complete the funnel or might not be tracked properly. If you simply discard incomplete observations, you can create bias if the missingness is not random. Non-random missingness (missing not at random, or MNAR) can systematically skew your results, causing the test’s assumptions to break down.
Possible strategies:
Imputation: For example, you might impute missing values based on mean, median, or model-based predictions. However, incorrectly specifying an imputation model can bias the distribution and p-values.
Multiple imputation: You impute several plausible datasets, run your hypothesis tests on each, and then pool the results. This helps account for the uncertainty in imputation.
Sensitivity analysis: Investigate how different missing-data assumptions change the outcome. If you find that small changes in the imputation procedure drastically shift the p-value, you know your test result is sensitive to the missing data process.
In short, missing data can add complexity and uncertainty. If not addressed properly, it can lead to either inflated or deflated p-values, and your final inferences may be invalid.
How do we interpret p-values in the context of adaptive or sequential experimentation?
Many real-world ML experiments do not collect data in a single batch. Instead, product teams might want to terminate or pivot an experiment early if results appear conclusive or if performance looks dismal. However, sequentially monitoring the p-value after each batch of data (often called “peeking”) inflates the Type I error rate. Because we are effectively doing multiple tests over time, the chance of incorrectly rejecting the null at least once increases.
Adaptive or sequential designs (such as group sequential methods or techniques like alpha-spending functions) give formal ways to monitor and stop trials early while controlling the overall Type I error. In these designs:
The experiment plan explicitly states at which points you will check the data and how you will adjust your significance threshold.
Methods like O’Brien-Fleming or Pocock boundaries define how to spend your alpha across multiple interim analyses.
Alternatively, a fully Bayesian approach can track posterior distributions rather than repeated p-values.
A common pitfall is to check the p-value daily and stop as soon as it dips below 0.05. This practice can lead to a much higher false-positive rate than 5%. Proper sequential or Bayesian methods ensure you can adapt in an online environment while still having valid inferences.
Can p-values alone determine real-world decisions, or do we need effect sizes and confidence intervals?
P-values by themselves only provide a gauge of how incompatible your data appear with the null hypothesis. They do not quantify the size of the effect. You can have a very small p-value with a trivially small difference in means or proportions if the sample size is large. Conversely, you might have a “borderline” p-value with a large effect size if your sample size is small, leaving you with high uncertainty.
Professional practice typically involves examining:
Effect size: This could be the raw difference in means (like a 5% increase in click-through rate) or standardized differences (Cohen’s d, etc.). A large effect size can be valuable in practical terms even if the p-value is borderline.
Confidence intervals (CIs): A 95% CI for the difference in means or proportions shows the range of plausible values given the observed data. If it’s narrow and far from zero, that gives strong evidence of a meaningful effect. If the interval is wide, your data may not be sufficiently precise to draw a robust conclusion, even if the p-value is small or large.
Decision-making in an ML environment often factors in cost, user experience, product design considerations, and risk tolerance. A purely statistical approach that looks at p-values alone can overlook these pragmatic aspects.
What strategies can be used to avoid over-reliance on p-values in an ML context?
Although p-values are a mainstay of statistical testing, modern ML practices sometimes emphasize alternative or complementary techniques:
Bayesian approaches: Instead of p-values, Bayesian analysis uses posterior probability distributions to show how likely a parameter (e.g., the difference between two treatments) is to lie above or below a certain threshold.
Estimation-focused approaches: Emphasizing confidence intervals or credible intervals over yes/no significance decisions.
Effect size and ROI analysis: A real-world question might be “If we launch this feature, do we expect at least a 2% improvement in user engagement?” You can compare your observed effect or posterior distribution to that threshold.
Likelihood ratios: Likelihood ratio tests or information criteria (AIC, BIC) can sometimes be more direct for comparing model fits without relying solely on p-values.
Cross-validation or out-of-sample performance: In purely predictive ML contexts, performance metrics like accuracy, precision, recall, or AUC on holdout sets or cross-validation folds might be more relevant than p-values about parameter significance.
A pitfall is to treat p-values as the only yardstick of success. Many advanced ML methods—such as neural networks, tree-based ensemble methods, or large language models—do not inherently produce p-values for their predictions; they rely on metrics and confidence estimates of predictive performance. When doing A/B tests, yes, p-values are common, but that is typically just one piece of the entire model-evaluation puzzle.
How should we address the possibility of publication bias or selective reporting in ML experiments?
In a corporate setting, teams might run experiments but only internally publicize or share the “success stories.” Similarly, academic research can sometimes face publication bias where papers with significant p-values are more likely to be accepted for publication. This selective reporting can distort the perceived success rate of proposed techniques.
Some ways to combat this:
Pre-registration: Define your hypotheses, metrics, and analysis plan before you see the data. Document them. Then, even if the results turn out to be non-significant, you still share them.
Reproducible pipelines: Keep a robust pipeline with version-controlled data, analysis scripts, and environment settings so that internal or external stakeholders can verify that no hidden “forking paths” or selective analyses were done.
Embrace negative or null results: In some development teams, a “null result” might be equally valuable because it prevents wasted resources on a non-effective feature. Transparent reporting helps the organization make well-informed decisions across multiple experiments.
A subtle pitfall is that teams might not see negative results from other groups or time periods and thus replicate mistakes. This can be especially problematic in big companies with many teams. Having a central registry of experiments—both successes and failures—can reduce the risk of duplicating efforts.
How do we use p-values in the presence of confounders or multi-variate settings?
Many real-world problems involve more than one factor influencing an outcome. Suppose you are testing the effect of a new model interface on user satisfaction, but user demographics or device types are also strongly correlated with satisfaction. If these are not balanced between the control and treatment groups, a simple univariate test might give a misleading p-value.
Common approaches:
Randomization with stratification: Pre-stratify or block on known confounders (e.g., device type: iOS vs. Android) to ensure balanced representation across groups.
Multivariate regression modeling: A linear or logistic regression can include confounding variables as additional predictors. The p-value for your “treatment” variable in this model accounts for partialing out the effects of confounders.
Propensity score matching (in observational studies): Match or weight subjects in the treatment and control groups to create a pseudo-randomized effect, then compute p-values after balancing.
Causal inference methods: Tools like difference-in-differences, instrumental variables, or synthetic controls can help if standard randomization was not feasible.
A pitfall is ignoring confounders and assuming your experiment is purely random or ignoring differences in user populations. Another subtlety is overfitting a model with too many covariates, which can produce artificially small p-values for some terms just by chance. Rigorous validation and domain understanding are key.
How do we interpret p-values when dealing with classification thresholds and multiple metrics?
In ML tasks, you might have multiple metrics—precision, recall, F1-score, ROC-AUC, etc.—and various classification thresholds you tune for a model. If you test each combination of threshold and metric for significance, you inflate Type I error due to multiple comparisons.
Potential approaches:
Pre-specify a primary metric: For instance, if recall is critical for your application, define recall at a specific threshold as your primary metric before testing anything else.
Use corrections for multiple hypotheses: If you must compare multiple metrics or thresholds, you can apply methods like Bonferroni or Holm-Bonferroni to adjust your significance level.
Multivariate or rank-based methods: In some advanced scenarios, you can define a single composite objective that captures multiple performance aspects.
A real-world pitfall is that teams might keep adjusting the classification threshold until they see a “significant” difference, inadvertently p-hacking their results. A more robust method is to fix the threshold selection method (e.g., maximizing F1 on a validation set) before you perform any final hypothesis test.
How do seasonal or time-dependent trends affect p-values in A/B tests?
Seasonality or trending behavior over time can influence performance metrics. For instance, user engagement might be higher during weekends or holidays. If your A/B test does not account for these trends, your p-value might reflect differences in seasonality rather than differences caused by the experimental variant.
Potential strategies include:
Randomization with time blocking: Launch control and treatment variants simultaneously across the same time intervals.
Use difference-in-differences: For each time window or day, collect baseline from control vs. treatment, then look at changes over time.
Wait for full seasonal cycles: If your product experiences strong weekly or monthly cycles, ensure your test runs for enough time to capture them.
Use a time-series approach: Model seasonality explicitly (e.g., with seasonal ARIMA) and evaluate the incremental effect of the treatment as an additional component.
A hidden pitfall arises if you run an experiment for too short a window during, say, a holiday surge, and incorrectly generalize the result. That can lead to spurious significance or missing the true effect that you’d see during normal periods.
How might we handle extremely low-frequency events?
Some metrics—like rare adverse events or extremely large purchases—occur only infrequently. When dealing with low-frequency data, standard asymptotic approximations used to derive p-values (like those in a typical z-test for proportions) may not hold. The distribution might be heavily skewed, and zero counts might be common.
In these cases:
Exact tests: Techniques like Fisher’s Exact Test can be used for categorical data with low counts.
Bootstrapping: You can bootstrap (resample) your dataset many times to empirically approximate the distribution of your metric and derive an empirical p-value.
Aggregated metrics: You might consider combining multiple similar outcomes or extending the time window to capture more events, though that risks mixing in confounders or ignoring time dynamics.
A pitfall is concluding no effect just because the data are too sparse to detect small differences. With extremely rare events, you might need a much larger sample or a longer observation period to achieve sufficient statistical power.
What are potential issues if the p-value threshold is changed after seeing results?
It’s a common temptation: an experiment yields a p-value of 0.06 under a significance threshold of 0.05, and the team says, “Well, 0.06 is close. Let’s just adopt 0.10 or 0.06 as our new threshold.” This is a form of “significance chasing.” It undercuts the principle that the significance level ((\alpha)) should be set before observing data. If you adapt (\alpha) based on the observed results, you can no longer interpret the p-value as you originally intended.
A direct real-world pitfall is that repeated flexible changes to the p-value threshold effectively p-hack the experiment, leading to inflated false-positive rates. If you must adapt or deviate from the initial plan for legitimate reasons, you should document the rationale and note that the resulting p-values are “exploratory” rather than confirmatory. In many regulated industries (like pharmaceuticals), changing (\alpha) post-hoc is simply disallowed because it invalidates claims about Type I error control.
When do non-significant p-values still lead to important insights?
Failing to reject the null hypothesis (i.e., obtaining a large p-value) is not necessarily uninformative. Sometimes, a non-significant result—especially one accompanied by a narrow confidence interval around zero—can suggest that if there is an effect, it’s likely small and might be of no practical consequence. That can guide business or product decisions: maybe there is no justification for rolling out a new feature if it doesn’t appear to meaningfully change a core metric.
However, a non-significant result with a very wide confidence interval could indicate a lack of data or power to draw meaningful conclusions. In that scenario, the correct takeaway is not that “there’s no effect” but rather “the data are inconclusive.” Additional data collection or improvements to the experiment design could be warranted.
Real-world subtlety: Even if the p-value is > 0.05, you might glean valuable knowledge about the effect’s plausible range. If the confidence interval is large but includes a moderate or large positive effect, you might want to refine the experiment or collect more data to confirm or refute that possibility.
How do domain-specific cost functions interact with p-values?
In many ML applications, the cost of false positives vs. false negatives can differ greatly. For example, in fraud detection, a Type II error (failing to catch fraud) might be extremely costly, whereas a Type I error (flagging a genuine transaction as fraud) might be less costly or equally costly but in different ways. P-values reflect the probability of data given the null, but they don’t inherently encode domain-specific cost functions.
An extremely small p-value might justify a decision to adopt a new system, but if the cost of false alarms or the risk to user experience is high, you might still proceed more cautiously. In other words:
High cost of Type I: You might choose a more stringent (\alpha) (e.g., 0.01 or 0.001) to reduce the risk of adopting a harmful change.
High cost of Type II: You might accept a more relaxed significance threshold to avoid missing a potentially valuable improvement.
In practice, data scientists often weigh business priorities and potential upside/downside alongside p-values or confidence intervals, forging a more holistic approach to making decisions.
Why might we consider effect sizes or Bayesian posterior probabilities in addition to p-values?
Effect sizes and Bayesian posterior probabilities can provide more intuitive insights:
Effect sizes show how large the impact is, which helps gauge practical importance rather than just the presence or absence of significance.
Bayesian posterior probabilities let you phrase conclusions like “We have a 95% probability that the improvement is at least 2%,” which can be more directly aligned with business or product goals than saying “We reject the null hypothesis at p < 0.05.”
In a real-world ML environment, telling stakeholders “the new recommendation algorithm has a 2.5% chance to be worse than the existing one and a 97.5% chance to be better” might resonate more than “the difference was statistically significant at the 5% level,” especially if decisions involve risk tolerance and ROI.
A pitfall in purely frequentist approaches is that p-values alone cannot straightforwardly express statements about the probability that a hypothesis is true; they are statements about data given the hypothesis. Bayesian approaches can tackle that question directly (with prior assumptions), but this requires careful choice of priors and might be computationally more complex.
How can we ensure that p-value results are robust across different data segments?
You might find a significant difference overall, but it could be driven primarily by a single segment of users (e.g., a certain geographic region, device type, or user demographic). Investigating segment-level differences (also known as subgroup analysis) is common and can be illuminating. However, repeatedly slicing the data by many factors can lead to multiple comparisons problems. The more segments you examine, the higher the chance of finding a spurious significant effect somewhere.
Techniques to address this:
Pre-specify key segments you are interested in analyzing based on domain knowledge (e.g., region, device type).
Use hierarchical or multi-level models that allow partial pooling across segments, improving estimates in segments with less data.
Apply corrections for multiple testing if you plan to do many subgroup analyses.
A subtle real-world pitfall is that data scientists discover a strong effect in one small segment post-hoc and present that as an important insight, but it might be noise. If it’s purely exploratory, it should be labeled as such, and a follow-up experiment might be needed to confirm the effect in that segment.
Under what circumstances might a p-value misrepresent the “practical risk” of adopting a new model?
P-values revolve around the idea of the null hypothesis and the probability of seeing the observed data if the null is true. Even if p < 0.05, an ML model that’s “better on average” might have worst-case performance scenarios that harm certain subsets of users or degrade performance in high-stakes situations.
Consider a text-generation model that is 5% better on standard benchmarks, with a p-value < 0.01. If there is a 0.5% chance it generates highly offensive or problematic content, that might be unacceptable from a brand or user experience perspective. The p-value from your A/B test that measured average user satisfaction does not necessarily capture that risk. Real-world product decisions often incorporate fairness, risk tolerance, or compliance considerations.
One subtlety is that you can design metrics that incorporate risk. For instance, you might measure not only the mean outcome but also the worst decile or some safety-critical threshold. The p-value on that specialized metric might be more relevant to your real concerns, but it might not align with a classical approach that focuses on average differences.
How does the choice of test statistic impact the resulting p-value?
Hypothesis testing can use different test statistics: the difference in means, difference in medians, or more complicated metrics. Choice of test statistic can change how sensitive the test is to certain effects. For example:
If the data are heavily skewed with outliers, a test based on means might be overly influenced by large but rare observations, potentially affecting the p-value’s stability.
A rank-based non-parametric statistic (like the Wilcoxon rank-sum for two independent samples) might be more robust to outliers, but less sensitive to differences in distribution tails.
In large-scale ML contexts, you might measure metrics like the AUC of a classifier. The variance of such metrics is not always straightforward; specialized tests or bootstrapping can be used to approximate the distribution of the AUC.
A real-world pitfall is blindly applying a test statistic or formula that was taught in a standard class (e.g., t-test) without validating that the underlying assumptions apply to your specific ML-based or domain-specific metric.
Are there scenarios where effect direction flips depending on the data sample, and how does that affect interpreting p-values?
Sometimes, an effect might appear positive in one subset of data and negative in another—this is akin to Simpson’s paradox, where the sign or magnitude of an effect can change when data is aggregated vs. disaggregated. P-values do not inherently warn you about such phenomena. If you only look at the overall aggregated p-value, you may miss that in certain subgroups (like new vs. returning users) the effect direction is reversed.
In ML model deployment, you could inadvertently degrade user experience for a major segment while improving it for another. Or, you might average out to an overall improvement but create fairness or equity issues. Therefore, it’s critical to do a thorough exploratory analysis of possible effect modifiers. Where relevant, you can run separate hypothesis tests or use models that include interaction terms (subgroup × treatment). If you do multiple subgroup analyses, remember to correct for multiple comparisons or treat those analyses as exploratory.
A subtle point is that if you break down your data to hunt for interesting patterns only after an overall test, you might need to do fresh confirmatory tests on new data to validate those patterns. Otherwise, you risk capitalizing on chance variations in the particular sample at hand.
What if p-values conflict with domain knowledge or prior evidence?
If domain experts strongly believe that a certain change should not have any effect, yet your test yields a tiny p-value, you may be seeing a chance anomaly, data contamination, or an unexpected confounding factor. Alternatively, it might be that the domain experts’ assumption was incomplete. In such conflicts, it’s wise to:
Double-check your data pipeline, randomization procedures, and potential confounders.
Re-run or replicate the experiment, if feasible.
Consult domain experts more closely to see if there could be an unaccounted-for mechanism that explains the effect.
P-values are purely statistical, and domain knowledge might reveal that the effect is biologically or physically implausible. Conversely, domain experts might not have considered certain dynamic influences. Either way, replicating or collecting additional data helps resolve the disagreement. Blindly trusting or dismissing the p-value can both lead to errors.
What are some best practices for documenting p-values in final reports or internal dashboards?
In many tech companies, experiment results are shared through dashboards or analytics tools. Some recommendations for best practice:
Always provide sample sizes and effect sizes along with p-values.
Include confidence intervals for the metric differences.
Document the exact test used (t-test, z-test, non-parametric test, or a regression approach) and mention any assumptions.
Specify the alpha level that you used and whether you corrected for multiple comparisons.
If it’s a sequential test, mention how many times the data were “peeked at.”
Provide disclaimers if any known confounders or data limitations exist.
A subtle pitfall is presenting a p-value in isolation on a dashboard without context. Stakeholders might misinterpret its meaning or treat it as a conclusive, all-encompassing statement about the success or failure of a change. Transparent, thorough documentation reduces that risk.
How can we address noisy labels or measurement errors that might dilute p-values?
In some ML scenarios, your response variable might be noisy or your user feedback might be incomplete. Even if your experiment is well-designed, label noise can inflate the variance of your estimates, potentially leading to higher p-values (less chance of seeing a significant effect) or unpredictable bias.
Possible strategies:
Improve measurement: Better instrumentation or multiple measurement methods (e.g., collecting both direct user feedback and indirect usage metrics) can reduce noise.
Data cleaning: Remove or correct suspicious data points if you have strong evidence that they are erroneous.
Noise-robust metrics or transformations: If the distribution of noise is known or if outliers are frequent, a robust method (like median-based or rank-based tests) might yield more reliable p-values.
Larger sample: Sometimes, the simplest solution is to increase your sample size to wash out random noise.
A pitfall arises when you suspect you have “noisy data” but do not investigate the source of that noise. You might miss a real effect or interpret a spurious pattern as evidence of an effect. Proper diligence in data collection and validation is essential.
Could certain resampling or simulation methods be used to validate or refine p-values?
Yes. Bootstrap and permutation methods are popular in data science to empirically estimate the distribution of a test statistic:
Permutation tests: Randomly shuffle labels (e.g., treatment vs. control) under the assumption that the null hypothesis is true and compare the observed test statistic to the distribution of shuffled outcomes.
Bootstrap: Re-sample with replacement from the observed data multiple times, each time calculating the difference in means (or other metrics). This yields an empirical distribution of the difference, from which a p-value can be approximated.
These methods can be especially useful if you lack confidence in the parametric assumptions of a standard test or if your data come from complex distributions. The main pitfall is computational cost—bootstrapping or permutation tests can be expensive for large datasets. Also, if the data collection process or randomization was flawed, resampling methods still replicate that flaw. Hence, the correctness of these approaches rests on the assumption that the original dataset is representative and that the labeling or grouping was done appropriately.
When might p-values be misleading in online recommendation systems?
Online recommendation systems often use multi-armed bandit approaches that adaptively shift traffic to the better-performing variant. Traditional p-values rely on fixed-allocation designs. If you feed more traffic to the current best performer as the experiment progresses, you are no longer sampling identically or independently from each arm. This adaptive data collection violates standard test assumptions for computing p-values.
A real-world subtlety is that multi-armed bandit algorithms prioritize optimizing cumulative reward over rigorous inference of significance. If you want both optimization and valid inference, you may need specialized methods (like Thompson sampling with Bayesian posteriors or group sequential frequentist methods). If you try to apply a standard p-value approach at the end of a bandit experiment, the Type I error is typically not well-controlled because of the repeated adaptation.
Is there a risk in conflating correlation with causation when interpreting p-values?
Yes. Even in an experiment that is believed to be randomized, unrecognized biases or unintentional selection effects could mean that your observed difference correlates with the treatment but is not fully caused by it. A p-value only tells you how surprising the data are under the null hypothesis; it doesn’t automatically prove that the observed difference is purely causal. Good experimental design and randomization help, but real-world complexities (unequal dropout rates, imperfect randomization, user self-selection, etc.) can reintroduce confounding.
In observational studies (where you didn’t randomly assign treatments), a small p-value might just reflect correlation. You must be extra cautious in concluding causality. Adjustments with regression or propensity scores help but do not guarantee the confounders have all been accounted for. This is a major pitfall in ML where observational data are abundant and experiments might be logistically difficult to run. Always remember that a statistically significant correlation does not necessarily imply a direct cause-and-effect relationship.
How can we handle scenarios where the p-value approach is not the most appropriate?
Sometimes, you might be dealing with:
Non-standard outcomes (like user behavior distributions that are extremely skewed or multi-modal).
Complex dependencies (like network effects where one user’s treatment status affects another user’s outcome).
Very high-dimensional parameter spaces (like large-scale model parameter comparisons).
In these scenarios:
Bayesian methods: Provide a flexible framework for modeling complicated data structures and directly obtaining posterior distributions.
Simulation-based methods: If you can simulate from your model or environment, you might evaluate performance metrics more directly rather than relying on a closed-form p-value.
Machine learning model comparisons: Out-of-sample performance measures with cross-validation or nested cross-validation might be more transparent or robust than focusing on a single p-value for the difference in performance.
A pitfall is to shoehorn everything into a classic hypothesis testing framework when the real problem might be better served by more specialized approaches. Proper method selection depends on the exact nature of the data, the experiment design, and the business or product question at hand.