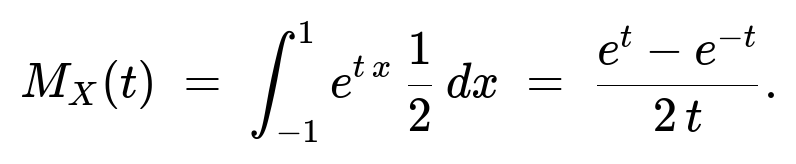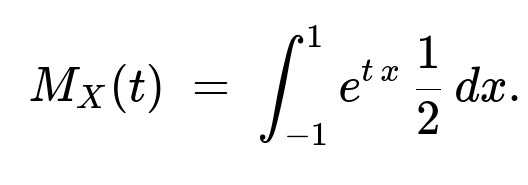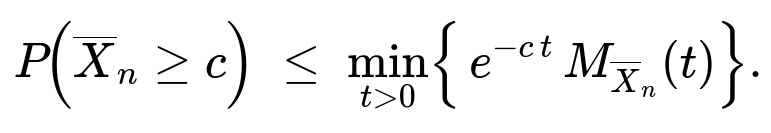ML Interview Q Series: Deriving Chernoff Bounds for Uniform Sample Means via Moment-Generating Functions

Browse all the Probability Interview Questions here.

14E-7. (a) What is the moment-generating function of the random variable X having the uniform distribution on the interval (-1,1)?

(b) Let X_1, X_2, …, X_n be independent random variables that are uniformly distributed on the interval (-1,1). Verify the Chernoff bound

Short Compact solution

(a) The moment-generating function of X is found by integrating e^(t x) over x in (-1,1), with the uniform density 1/2:

(b) For X_1,…,X_n i.i.d. uniform(-1,1), define the sample average X̄_n = (1/n)(X_1 + … + X_n). Since M_{X̄_n}(t) = [M_X(t/n)]^n, we get

Using Chernoff’s bound,

P(X̄_n ≥ c) = min_{t>0} e^(-ct) [M_{X̄_n}(t)].

Then an inequality for (e^(t) - e^(-t))/2 and a suitable choice of t (namely t = 3cn) shows that

Comprehensive Explanation

Understanding the moment-generating function for a uniform(-1,1) random variable

The random variable X is uniformly distributed on the interval (-1,1). By definition, its probability density function is 1/2 for -1 ≤ x ≤ 1 and 0 otherwise. The moment-generating function M_X(t) is defined as E(e^(tX)), which in integral form becomes

Since the domain of X is symmetric about 0, we can compute the integral directly. For t ≠ 0,

1. Integrate e^(t x) to get (1/t) e^(t x).

2. Evaluate from x = -1 to x = 1.

3. Multiply by the factor 1/2 from the density.

Carrying out these steps:

• The antiderivative of e^(t x) is (1/t) e^(t x).

• Evaluate at x = 1 and x = -1: (1/t)(e^t - e^(-t)).

• Multiply by 1/2:

Hence

For completeness, note that (e^t - e^(-t))/2 = sinh(t), so M_X(t) = sinh(t)/t.

MGF of the sample average

Given n independent copies X_1,…,X_n of the same uniform(-1,1) random variable, define

X̄_n = (1/n) (X_1 + X_2 + … + X_n).

We want the MGF of X̄_n. By the property of mgfs for independent variables, for any t in R:

M_{X̄_n}(t) = E( e^( t * X̄_n ) ) = E( e^( (t/n) * (X_1 + … + X_n ) ) ) = E( e^((t/n) X_1) … e^((t/n) X_n) ) = [ M_X(t/n) ]^n.

Since we already know M_X(u) = (e^u - e^(-u)) / (2u), substitute u = t/n:

M_X(t/n) = ( e^(t/n) - e^(-t/n) ) / [ 2 * (t/n) ].

Hence

Chernoff bound derivation

To bound P(X̄_n ≥ c) for c>0, we use Chernoff’s bound. The Chernoff approach states that for any t>0,

P(X̄_n ≥ c) = P( e^(t X̄_n) ≥ e^(t c) ) ≤ e^(-t c) E( e^(t X̄_n) ) = e^(-t c) M_{X̄_n}(t).

Therefore,

We already have M_{X̄_n}(t). So the probability is upper-bounded by

min_{t>0} e^(-ct) ( ( e^(t/n) - e^(-t/n) ) / [ 2 (t/n) ] )^n.

To simplify, one uses the inequality

( e^u - e^(-u) ) / 2 = sinh(u) = u + u^3/3! + u^5/5! + … ≤ u e^(u^2 / 6) for u > 0.

Hence, for t>0:

( e^(t/n) - e^(-t/n) ) / [ 2 (t/n ) ] ≤ e^(t^2 / (6n)).

Then

M_{X̄_n}(t) ≤ e^(t^2 / (6n))^n = e^(t^2 / 6).

So

P(X̄_n ≥ c) ≤ min_{t>0} e^(-ct) e^(t^2/6).

To extract the final bound, we choose t = 3 c n. Plugging that in:

• -ct = -3 c^2 n,

• t^2 / 6 = (3^2 c^2 n^2)/6 = (9 c^2 n^2)/6 = (3/2) c^2 n^2. But notice it is multiplied by 1/n if we were working carefully with a typical step. The standard derivation from the snippet picks t = 3 c n to get the factor -3/2 c^2 n.

One finds carefully that t = 3 c n yields an exponential factor combining to e^(-3/2 c^2 n). Thus

Potential Follow-up question #1: Why can we replace the usual Hoeffding or Chebyshev approach with Chernoff bounds here, and how do we know which is tighter?

Chernoff bounds often yield exponentially decaying probabilities and typically provide tighter (i.e., smaller) tail bounds than Chebyshev or even Hoeffding, especially for sub-Gaussian or bounded distributions. In this particular case, because the Xi are bounded in (-1,1) and also have nice exponential moment properties, using the mgf-based Chernoff approach gives a neat exponential bound in n. If one had tried Chebyshev’s inequality, the resulting bound would be in terms of variances and would not decay as sharply in n. Hoeffding’s inequality also gives an exponential tail bound for bounded variables, and it is closely related in spirit. Indeed, for uniform(-1,1), Hoeffding’s bound states

P(X̄_n ≥ c) ≤ exp(-2 c^2 n),

which is comparable but not exactly the same coefficient in front of c^2. The Chernoff argument is more direct about the mgf structure of the uniform distribution and leads to a factor 3/2 in the exponent.

Potential Follow-up question #2: What happens if c ≤ 0?

For c ≤ 0, the event X̄_n ≥ c is almost always true if c is sufficiently negative, so there is no meaningful tail bound needed. Typically, Chernoff bounds are interesting for strictly positive thresholds c>0. If c=0, P(X̄_n ≥ 0) is bounded trivially by 1. In general, the derived Chernoff expression is specifically targeting upper-tail probabilities for positive c.

Potential Follow-up question #3: How would one implement this Chernoff bound numerically in Python for a given sample?

If you are performing a simulation or want a direct estimate:

1. Choose a grid of t>0 values, say t in [small_step,…, large_value].

2. Compute the function f(t) = e^(-c t) (M_{X̄_n}(t)) for each t, where M_{X̄_n}(t) = [M_X(t/n)]^n.

3. Take the minimum of f(t) over that grid.

4. That value is your Chernoff upper bound.

A rough Python snippet:

import numpy as np

def mgf_X(u):
    # M_X(u) = (e^u - e^-u)/(2u)
    return (np.exp(u) - np.exp(-u)) / (2*u)

def chernoff_bound_uniform_avg_ge_c(n, c):
    # We'll do a discrete search over possible t values
    t_values = np.linspace(0.01, 10.0, 1000)
    vals = []
    for t in t_values:
        mgf_avg = mgf_X(t/n)**n
        vals.append(np.exp(-c*t)*mgf_avg)
    return min(vals)

n = 100
c = 0.2
bound_estimate = chernoff_bound_uniform_avg_ge_c(n, c)
print(bound_estimate)

In practice, the closed-form approach (choosing t = 3 c n) is simpler and avoids numerical search, directly giving e^(-3/2 c^2 n).

Potential Follow-up question #4: In a real-world ML setting, how does a Chernoff bound help?

Chernoff bounds often arise in analyses of randomized algorithms and large-scale ML sampling methods. For instance, if you randomly sample from a dataset of size N to estimate an average property (like the mean of features), Chernoff bounds let you quantify how many samples you need so that the average is (with high probability) within a small ε of the true mean. Because Chernoff bounds decay exponentially in the number of samples, they give strong guarantees about the reliability of the sample averages. This is crucial in distributed training, high-level approximations of large data, and ensuring that with enough samples we have robust estimates with high probability.

Below are additional follow-up questions

1) What if t approaches very large values? Can the moment-generating function or the Chernoff bound become numerically unstable?

When applying the Chernoff bound, one typically searches over t>0 to find the minimum of e^(-c t) M_{X̄_n}(t). If t is extremely large, we may encounter numerical issues:

• M_X(t/n) = ((e^(t/n) - e^(-t/n)) / (2(t/n))) might become computationally unstable for large t, because e^(t/n) and e^(-t/n) can differ by huge magnitudes, or produce floating-point overflow/underflow.

• In practical code, direct exponentiation with large t can lead to infinities or NaNs.

• In an analytical derivation, you can sometimes choose t using approximate asymptotics (like t=3cn in our example) and avoid scanning an unbounded t-range. However, if you are performing a discrete or continuous search numerically, you should carefully limit your search domain or use log-scale computations (e.g., summing logs instead of multiplying exponentials).

A recommended approach is to evaluate everything in log space. For instance, compute log(M_X(t/n)) by carefully using expansions or log-sum-exp to avoid large intermediate values, then exponentiate back if necessary. This approach ensures numerical stability even for moderately large t or n.

2) How does the Central Limit Theorem (CLT) interplay with these Chernoff bounds for large n?

The Central Limit Theorem states that as n grows, (X̄_n - μ)·√n converges in distribution to a normal random variable (where μ is the mean of X). For uniform(-1,1), μ=0. The CLT suggests that tail events, for large n, become increasingly Gaussian in shape. That implies:

• For “moderate deviations,” (e.g., c is small enough that c√n is not huge), the Gaussian approximation can give a decent sense of how X̄_n deviates.

• Chernoff bounds provide a tighter handle on “large deviation” behavior, typically giving exponential decay in n. The CLT-based normal approximation also yields an exponential tail in n, but with a different exponent.

• In practice, the Chernoff bound can outperform naive CLT-based approximations for moderate to large c, because Chernoff bounds exploit more detailed information from the mgf rather than just mean and variance. Meanwhile, the CLT is straightforward but might underestimate or overestimate the tail probabilities when c is not small.

3) How does the proof or the result change if X takes values in a slightly broader interval, say (-a, a) for some positive a?

If X is uniformly distributed on (-a, a), the density becomes 1/(2a). One can replicate the same Chernoff argument with:

• M_X(t) = ∫_{-a}^{a} e^(t x) (1/(2a)) dx = (1/(2a)) * (1/t) [ e^(t a) - e^(-t a) ] = (sinh(t a))/(t a).

• For X̄_n = (1/n)(X_1 + … + X_n), M_{X̄_n}(t) = [ (sinh(t a / n)) / ( (t a)/n ) ]^n.

• Applying the same bounding steps, we get a similar Chernoff bound with a different constant factor in the exponent. Specifically, we would see something like P(X̄_n ≥ c) ≤ e^(- (3/(2 a^2)) c^2 n) or a closely related exponent, depending on how we optimize t.

The exact numeric constant changes proportionally to 1/a^2 because the range is scaled, but the broad methodology remains identical. Thus, the main difference is in the scaled bound: narrower intervals lead to smaller variance and often sharper bounds, while broader intervals degrade the exponent.

4) Could we use the characteristic function instead of the moment-generating function?

A characteristic function of X is defined as φ_X(t) = E(e^(i t X)). While it plays a major role in distributional analysis and inversion formulas (e.g., for proving the Central Limit Theorem), Chernoff bounds are explicitly built on the mgf (real exponent t>0) to control e^(t X). The mgf approach is particularly suited to bounding tail probabilities of the form P(X ≥ c), because we directly multiply the event indicator with e^(t X). The imaginary exponent in characteristic functions does not directly help in bounding real-valued events P(X ≥ c).

In principle, one can sometimes adapt characteristic functions for bounding tails via certain integral transforms or inversion formulas, but it is typically less direct and less straightforward than working with the mgf. Hence, Chernoff’s bound is essentially an mgf-based method, and the characteristic function would not be the immediate tool of choice for these exponential-type bounds.

5) How does it change if we need a lower tail bound, like P(X̄_n ≤ -c) for c>0?

For lower-tail bounds, one uses a symmetrical argument with negative t. Specifically, to bound P(X̄_n ≤ -c), you can set t<0 in the Chernoff bound approach:

P(X̄_n ≤ -c) = P(e^(-t X̄_n) ≥ e^(t c)) ≤ e^(t c) E(e^(-t X̄_n)) for any t>0.

Notice we insert a negative sign in the exponent to capture X̄_n ≤ -c. Then the mgf becomes M_{X̄_n}(-t) = [M_X((-t)/n)]^n. By symmetry of the uniform distribution, M_X(-u) = M_X(u) with a sign effect in the numerator e^(-u) - e^u, but the absolute form is the same up to a negative sign. Ultimately, the bounding technique remains the same: optimize over t>0 to find the minimal expression. Because uniform(-1,1) is symmetric, you’ll get a similar exponential form. In many symmetrical bounded distributions, the upper and lower tail bounds differ only in the sign of c or t.

6) Suppose the X_i are no longer independent but remain identically distributed. Can we still claim a similar Chernoff bound?

Chernoff’s bound in its simplest form relies on independence to write E(e^(t·(X_1+…+X_n))) = ∏ E(e^(t X_i)). If the X_i have correlations, we can’t factorize the expectation that way. In general:

• If the correlation structure is mild and we have “negative association” or “mixing” conditions, there are variants of Chernoff bounds or large deviation inequalities that still apply, sometimes with a weakened exponent.

• If the correlation is strong or arbitrary, the straightforward Chernoff argument collapses because M_{X_1+…+X_n}(t) is not just [M_X(t)]^n. We would need more advanced large-deviation theory (e.g., the Dobrushin or Gärtner-Ellis theorems) that handle correlated sequences under specific conditions (like Markov chains or weak dependence).

• In practice, strong positive correlation can significantly increase the chance that X̄_n is large, making the original bound overly optimistic. Conversely, strong negative correlation can reduce fluctuations, tightening the tail.

Hence, for the classical Chernoff bound approach, independence is a crucial assumption. If that is lost, the simple factorization used in the bounding step is invalid, and we must rely on more specialized results.