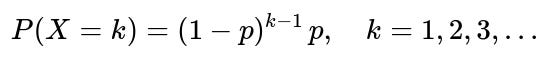ML Interview Q Series: Deriving Geometric Distribution Expectation Using Geometric Series Calculus.

Browse all the Probability Interview Questions here.

27. Derive the expectation for a geometrically distributed random variable.

Below is a comprehensive, in-depth explanation of how to derive the expectation (mean) of a geometrically distributed random variable. Following that, you will find potential follow-up questions (formatted with H2 headings) and exhaustive answers to them. Throughout this discussion, the focus is on a clear and thorough conceptual explanation. We minimize unnecessary repetition while still providing enough detail to cover subtle points that might arise in a FANG-type interview context. All code examples are in Python, and all mathematical expressions are rendered in LaTeX with the required syntax.

Thinking Process (concise, high-level overview without revealing private chain-of-thought): We start by clarifying definitions of the geometric distribution. Then we show step-by-step how to compute its expectation using the sum of an infinite series or other known techniques. We discuss the difference between two conventions of geometric distributions (one that counts the number of Bernoulli trials until the first success, and one that counts the number of failures before the first success). After deriving the expected value formula, we illustrate edge cases and typical pitfalls.

Explanation Begins:

Understanding the Geometric Distribution

The geometric distribution models the number of trials needed to get the first success in repeated Bernoulli trials with success probability p. There are two common parameterizations for a geometric random variable X:

• Parameterization A: X is the total number of trials needed to achieve the first success. Here, X∈{1,2,3,… }. • Parameterization B: X is the number of failures before the first success. Here, X∈{0,1,2,… }.

We will use Parameterization A, which is very common:

In this form, k represents the exact trial on which the first success occurs.

Deriving the Expectation

To derive the expectation (mean) of X, we use the following definition of expectation for a discrete random variable:

E[X] = sum over k from 1 to infinity of [k * P(X = k)]

We substitute the PMF for the geometric distribution:

P(X = k) = (1 - p)^(k-1) * p

so

E[X] = sum over k from 1 to infinity of [k * (1 - p)^(k-1) * p]

We can factor out p since it does not depend on k:

E[X] = p * sum over k from 1 to infinity of [k * (1 - p)^(k-1)]

Next, let r = 1 - p. Then the sum becomes:

E[X] = p * sum over k from 1 to infinity of [k * r^(k-1)]

We recognize a known power series identity. One standard approach is to note that for |r| < 1:

sum over k from 0 to infinity of [r^k] = 1 / (1 - r)

and by differentiating with respect to r (the so-called derivative trick), each term k * r^(k - 1) appears, giving:

sum over k from 1 to infinity of [k * r^(k - 1)] = 1 / (1 - r)^2

Hence:

E[X] = p * (1 / (1 - r)^2) = p * (1 / (1 - (1 - p))^2) = p * (1 / p^2) = 1 / p

Therefore, for the geometric distribution where X represents the trial number of the first success:

E[X] = 1 / p

If one used Parameterization B (the number of failures before the first success), then the random variable Y = X - 1, and its expectation would be:

E[Y] = E[X - 1] = (1 / p) - 1 = (1 - p) / p

This completes the derivation of the expected value for a geometrically distributed random variable.

Practical Code Example

Below is a simple Python code snippet illustrating simulations to empirically verify the mean of a geometric random variable using Parameterization A (number of trials until the first success). This snippet can help confirm that E[X] is approximately 1/p empirically:

import numpy as np

def simulate_geometric(p, num_samples=10_000_000):
    # Parameterization A:
    # Generate geometric random variables using built-in or custom approach
    # We'll use a custom approach here for illustration
    samples = []
    for _ in range(num_samples):
        count = 1
        while np.random.rand() > p:
            count += 1
        samples.append(count)
    return np.mean(samples)

p = 0.3
estimated_mean = simulate_geometric(p)
print("Empirical Mean =", estimated_mean, "Theoretical Mean =", 1/p)

In practice, using something like np.random.geometric(p, size=num_samples) can be much faster, but the above custom loop shows the concept.

Could you explain why differentiating the sum of a geometric series helps in deriving the expectation?

When computing the expectation E[X] = sum over k from 1 to infinity of [k * r^(k-1)], the term k * r^(k-1) appears naturally when taking the derivative of the standard geometric series. Specifically, if you start with

sum over k from 0 to infinity of [r^k] = 1 / (1 - r), valid for |r| < 1,

then differentiate both sides with respect to r. Each r^k becomes k * r^(k-1), and the right-hand side 1 / (1 - r) becomes 1 / (1 - r)^2. This identity is exactly what we need for evaluating the sum of k * r^(k-1). From a deeper perspective, this derivative trick is an efficient shortcut to handle infinite sums that would otherwise be more tedious to evaluate directly.

What if the geometric random variable was defined as the number of failures before the first success?

If X is defined as the number of trials up to and including the first success (Parameterization A), then E[X] = 1 / p. If Y is defined as the number of failures before the first success (Parameterization B), then Y = X - 1, so

E[Y] = E[X - 1] = (1 / p) - 1 = (1 - p) / p

It is essential to know which parameterization a particular library or reference is using. Many off-by-one errors happen when someone incorrectly assumes one parameterization when a library uses the other.

What are typical edge cases or pitfalls when using the geometric distribution?

One main pitfall is mixing up the two parameterizations. Another is ignoring that 0 < p <= 1, which is required for a proper geometric distribution. If p is extremely small, you can end up with very large values of X. If p is extremely close to 1, most of your samples for X will be 1. Both extremes can cause numerical or performance issues, so be mindful of that when simulating or using the distribution in real applications.

How would you simulate large-scale geometric data efficiently?

The main technique is to avoid pure Python loops and rely on vectorized implementations. NumPy, for example, provides np.random.geometric(p, size=N), which uses efficient native code under the hood. This is much faster than running a Python while-loop for each sample.

Can you relate the geometric distribution to a Bernoulli process and its memoryless property?

A Bernoulli process is a sequence of independent Bernoulli trials, each with probability p of success. The geometric distribution models the waiting time (number of trials) for the first success. It also has the memoryless property:

P(X > s + t | X > s) = P(X > t)

If s trials have passed with no success, the distribution of how much longer until the first success does not depend on s. Only the geometric and the exponential distributions share this memoryless property in discrete and continuous time, respectively.

Why is the memoryless property so critical in certain applications?

The memoryless property is important in situations where the future is conditionally independent of the past given the present, such as reliability testing where each new trial remains identical and independent of previous trials, or in modeling discrete-time arrivals where the probability of an arrival is constant each time period.

Could you also compute the expectation for the geometric distribution by summation without the derivative trick?

Yes. You could start from

E[X] = sum over k from 1 to infinity of [k * p * (1 - p)^(k-1)]

and then manipulate the partial sums of an infinite series. Eventually, by recognizing the structure of 1 + 2r + 3r^2 + ..., you arrive at the same identity that the sum is 1 / (1 - r)^2 for r = 1 - p. The derivative approach is simply a concise way of deriving the same result.

How would you explain the variance and other moments of the geometric distribution?

For X (the trial number of the first success) in Parameterization A, the variance is given by

Var(X) = (1 - p) / p^2

One way to derive this is to use E[X^2] - (E[X])^2 or known formulas for the negative binomial distribution, of which the geometric is a special case.

Is there a connection between the geometric distribution and the binomial or negative binomial?

Yes. The geometric distribution is a special case of the negative binomial distribution with r = 1 (i.e., when you only need 1 success). Both geometric and binomial distributions arise from repeated Bernoulli trials. The binomial distribution counts the number of successes in a fixed number of trials, whereas the geometric distribution models how many trials it takes to get a single success.

How can knowledge of the geometric distribution be applied in real-world engineering or product use cases?

A/B testing: The time or number of impressions until the first conversion can be geometric if each impression is an independent Bernoulli trial with probability p of converting.

Manufacturing defects: If each item has an independent probability p of being defective, the number of items produced until the first defective is geometric.

Queuing systems: In discrete-time queue models, the waiting time until the first arrival can be geometric if arrivals occur with a constant probability each time unit.

What if we consider partial knowledge of p or perform Bayesian inference for p in a geometric model?

You can place a Beta prior on p and observe data about how many trials occurred before success. Because the geometric likelihood is conjugate to the Beta prior (through the Bernoulli framework), updating the prior to a posterior is relatively straightforward. You can then sample from or analytically compute the posterior over p and make predictions about future waiting times.

Could you show a quick example of using PyTorch or TensorFlow Probability to sample from a geometric distribution?

PyTorch example:

import torch

p = 0.3
geom_dist = torch.distributions.Geometric(p)
samples = geom_dist.sample((1000,))
print(samples.float().mean().item())
print("Theoretical Mean:", 1/p)

TensorFlow Probability example:

import tensorflow_probability as tfp
import tensorflow as tf

tfd = tfp.distributions
p = 0.3
geom_dist = tfd.Geometric(probs=p)
samples = geom_dist.sample(1000)
mean_est = tf.reduce_mean(tf.cast(samples, tf.float32))
print(mean_est.numpy())
print("Theoretical Mean:", 1/p)

Note that some libraries use Parameterization B (the number of failures before success), so check the documentation to see if you need to adjust by 1.

Summarize why the expectation of a geometric distribution is 1/p

X counts the number of Bernoulli trials needed for the first success, each with probability p. From either a power series manipulation or a derivative approach on the infinite series, you get E[X] = 1 / p. Intuitively, if each trial has probability p of success, on average you expect about 1/p trials to achieve success.

Below are additional follow-up questions

How does the survival function of a geometric distribution help in practical scenarios?

The survival function (also called the tail probability) of a geometric distribution (Parameterization A) is the probability that the random variable X exceeds some value k. Concretely, for X = the trial on which the first success occurs, the survival function is:

S(k) = P(X > k) = (1 - p)^k

The reasoning is that for X to be greater than k, the first k trials must fail (each with probability 1 - p). In many real-world applications, such as reliability testing or A/B experiments, this survival function is used to determine the chance that no success (or desired event) has occurred by a certain time. It can be helpful in:

• Analyzing how likely it is that a user never converts up to a certain number of visits. • Estimating how many items you can produce before the first defect appears, with a given probability threshold.

A subtle pitfall is misinterpreting “greater than k” as “at least k successes” rather than “0 successes by time k,” so clarifying the meaning in your application is crucial.

What if the success probability p changes over time or depends on some external factors?

In many real-world processes, p can vary by trial (known as a non-stationary or time-varying process). The standard geometric distribution assumption is that p remains constant across trials. If p = p_i on trial i, the distribution of waiting times until first success is no longer strictly geometric. You might then define a discrete-time inhomogeneous process with:

P(X > k) = product from i=1 to k of (1 - p_i)

and

P(X = k) = (1 - p_1)(1 - p_2)...(1 - p_(k-1)) p_k

The expectation in that scenario must be computed using this more general PMF. One can no longer use the simple closed-form result 1 / p, because p is no longer constant. Instead, you would handle the random variable either by explicit summation or by simulation. Practically, you might consider:

• Adaptive probability models: p changes if external conditions (like environment, user behavior, or system states) shift. • Bayesian updating: if p is not known and you observe data over time, you can update beliefs about p in each trial.

A pitfall in a real project is to use a vanilla geometric model for data when p is clearly non-constant. This mismatch can lead to flawed inference or incorrect predictions.

Can we derive the moment generating function (MGF) of the geometric distribution and use it for insights?

Yes, the moment generating function of a geometric distribution (Parameterization A) with success probability p is:

M_X(t) = E[e^(tX)] = (p e^t) / (1 - (1 - p) e^t), for t < -ln(1 - p)

In plain text form:

M_X(t) = (p * exp(t)) / [1 - (1 - p) * exp(t)]

Using the MGF, you can obtain moments by taking derivatives of M_X(t) at t = 0. The first derivative at t = 0 yields E[X], and the second derivative helps compute E[X^2]. This approach can be helpful in advanced situations where sums of multiple geometric random variables are involved, or when you need higher-order moments. One subtlety is to make sure you keep track of the radius of convergence for t.

Is the geometric distribution unimodal, and why might that matter?

Yes, for the version where X = 1, 2, 3, ..., the geometric PMF typically has its highest value at X = 1. That is because the probability mass function p (1 - p)^(k - 1) is largest at k = 1, provided 0 < p <= 1. There is a single peak at k = 1, so it is unimodal.

In practice, unimodality matters because it tells you there is a single most likely outcome (the first trial is the success, if p is not extremely small). This helps to understand how the distribution shapes your real-world phenomenon: it suggests that the largest probability chunk is for success to happen very quickly. Nonetheless, if p is tiny, that peak is still the largest value, but the distribution's tail can extend very far.

How do we handle scenarios where p is extremely close to 0 or extremely close to 1 in implementations?

When p is close to 1, X is nearly always 1. This can lead to degenerate-like behavior (most samples are 1, so variance is very small). In software implementations, you might want to short-circuit logic if p is above some threshold, to avoid unnecessary computations.

When p is extremely small, the waiting time can be very large. This might trigger performance or memory issues in naive simulation approaches if you are repeatedly waiting for success. You could instead use a more efficient technique (like a direct inverse transform sampling approach) or place a cap and handle extremely large waits in a special manner.

A subtle pitfall is floating-point underflow in calculations like (1 - p)^(k - 1) if k is large. Libraries that have built-in geometric generators often mitigate this internally, but if you code your own approach, you have to be careful about potential numerical stability problems.

If we collect empirical data, how can we test if it follows a geometric distribution?

Statistically, you could:

• Use a chi-square goodness-of-fit test by binning your observed counts for each possible trial number. • Use a likelihood-ratio test or a Kolmogorov–Smirnov–type test adapted for discrete distributions. • Plot an empirical survival function on a log scale. For a geometric distribution (Parameterization A), log of P(X > k) = k * log(1 - p). If your data is roughly linear on a log scale, that’s indicative of a geometric tail.

A subtlety is ensuring you have enough data points, especially in the tail, to validate the geometric shape. If your data is truncated or you cannot observe very large values, your test might incorrectly reject or accept the geometric model due to incomplete tail information.

How does the concept of hazard rate apply to the geometric distribution, and how is it interpreted?

The hazard rate in discrete time is defined as:

h(k) = P(X = k | X >= k)

For a geometric distribution, h(k) = p (i.e., the constant probability of success on each trial, given that you have not succeeded yet). This constant hazard rate is another way of capturing the memoryless property. Practically, it indicates that your chance of “failure ending” (or success happening) per trial remains the same regardless of how many failures have already happened. This is crucial in settings like reliability or survival analysis, where you interpret p as the probability that a system fails (or a success occurs) in any given period, independent of how long it’s been running.

What if a process produces more zeros than the standard geometric model allows (a zero-inflated scenario)?

A zero-inflated geometric model would let you incorporate an extra mass at X=1 (Parameterization A) or X=0 (Parameterization B), beyond what a standard geometric distribution predicts. Concretely, you might say:

• With some probability alpha, X is 1 immediately (or 0 if we are in failures-before-success mode) no matter what. • Otherwise, you follow a standard geometric distribution with parameter p.

This can happen in real-world cases where there is a certain proportion of guaranteed “instant successes” or an external factor that forces success on the first try. Fitting a zero-inflated geometric model involves estimating both alpha (the probability of an immediate success) and p (the geometric success probability). A pitfall is ignoring that extra mass at 1 or 0, which can cause you to underestimate or overestimate p if you assume a pure geometric model.

If the independence assumption is violated, how does that affect geometric modeling?

If trials are not independent, the standard geometric model no longer applies directly. Correlation between trials means that the chance of success on the next trial might depend on whether previous trials were successes or failures. In such a case:

• The memoryless property breaks down. • You might need a Markov chain approach to model the transition probabilities from one state to another. • You can still attempt to approximate with a geometric distribution if correlations are weak, but you must be aware of potential bias in your estimates.

For instance, in a user behavior scenario, a user might be less likely to convert (success) after multiple failures if frustration sets in, or more likely if interest intensifies. Such feedback loops destroy the simple geometric assumption.

How do we combine or mix multiple geometric distributions in practice?

If you have different subpopulations or different contexts, each with a different success probability p_i, you could create a mixture of geometric distributions. Concretely, you might say:

• With probability w_1, X is geometric with p_1. • With probability w_2, X is geometric with p_2. • And so on, for multiple p_i summing to 1 in mixture weights.

The resulting mixture distribution is no longer purely geometric and typically loses the memoryless property. You can still compute the overall PMF as a weighted sum of each sub-geometry’s PMF. However, the expectation of the mixture is sum over i of [w_i * (1 / p_i)] for Parameterization A. A pitfall is trying to apply a single geometric to the entire data when in fact there are distinct subpopulations with different success probabilities. This mixture approach is often used in modeling heterogeneous user populations or systems with different operating conditions.