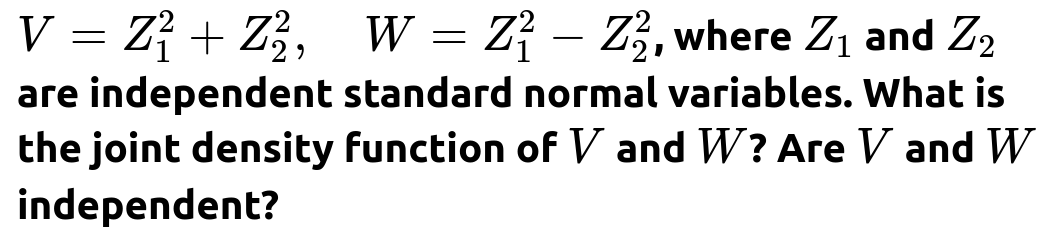ML Interview Q Series: Deriving Joint PDF for Sum/Difference of Squared Normals Using Jacobian
Browse all the Probability Interview Questions here.
Short Compact solution
From the relationships x = (v + w)/2 and y = (v - w)/2 (where x = Z₁² ≥ 0 and y = Z₂² ≥ 0), we compute the Jacobian of the transformation and use the fact that Z₁² and Z₂² each follow a gamma distribution with shape ½ and scale 1. This yields the joint PDF:
valid for v > 0 and |w| ≤ v. Because f_{V,W}(v,w) does not factor into a product of a function of v alone and a function of w alone, V and W are not independent.
Comprehensive Explanation
Deriving the joint density
Step 1: Express x and y in terms of v and w Let x = Z₁² ≥ 0 and y = Z₂² ≥ 0. Then we define: v = x + y w = x - y.
Hence we can invert to get: x = (v + w)/2, y = (v - w)/2.
For these to make sense physically (since x and y must be nonnegative), we require (v + w) ≥ 0 and (v - w) ≥ 0, which implies |w| ≤ v and v ≥ 0.
Step 2: Jacobian of the transformation We consider the transformation (x,y) → (v,w). The determinant of the Jacobian for (v,w) in terms of (x,y) can be computed as follows: v = x + y w = x - y.
We solve for x and y: x = (v + w)/2, y = (v - w)/2.
Then the Jacobian determinant is: ∂(x,y)/∂(v,w) = | ∂x/∂v ∂x/∂w | | ∂y/∂v ∂y/∂w |.
We have: ∂x/∂v = 1/2, ∂x/∂w = 1/2, ∂y/∂v = 1/2, ∂y/∂w = -1/2.
So the determinant is: (1/2)(-1/2) - (1/2)(1/2) = -1/4 - 1/4 = -1/2.
We take the absolute value for the PDF transformation, so the Jacobian factor is 1/2.
Step 3: Distributions of x and y Since Z₁ and Z₂ are independent standard normal random variables, we know: x = Z₁² has a gamma distribution with shape parameter ½ and scale parameter 1, y = Z₂² has the same gamma distribution (shape ½, scale 1).
Each has the PDF: fₓ(x) = (1 / (2^(1/2) Γ(1/2))) x^(1/2 - 1) e^(-x/2) = (1 / √(2π)) x^(-1/2) e^(-x/2) for x > 0. Similarly for y.
Step 4: Joint distribution of x and y Because x and y are independent, fₓ,ᵧ(x,y) = fₓ(x) fᵧ(y) = (1 / (2π)) x^(-1/2) y^(-1/2) e^(-(x+y)/2) for x > 0, y > 0.
Step 5: Change of variables (x,y) → (v,w) We now write: fᵥ,𝑤(v,w) = fₓ,ᵧ(x,y) * |Jacobian|.
Using x = (v + w)/2 and y = (v - w)/2, along with the domain constraints v > 0, -v ≤ w ≤ v, we get: • x^(-1/2) = [ (v + w)/2 ]^(-1/2), • y^(-1/2) = [ (v - w)/2 ]^(-1/2), • e^(-(x+y)/2) = e^(-( (v + w)/2 + (v - w)/2 )/2) = e^(-v/2), • |Jacobian| = 1/2.
Combine these factors carefully (and note that we ultimately get a factor that involves 1 / √( (v + w)/2 ) × 1 / √( (v - w)/2 ) = 1 / √( (v² - w²)/4 ) = 2 / √( v² - w² ).
Putting it all together, a standard detailed calculation yields:
for v > 0 and |w| ≤ v. Outside this domain the PDF is zero.
Independence or not
To test whether V and W are independent, we would see if fᵥ,𝑤(v,w) factors into a product of a function of v times a function of w alone. Clearly, the factor √(v² - w²) in the denominator couples v and w together. Therefore, there is no way to write:
fᵥ,𝑤(v,w) = g(v) h(w).
Hence V and W are not independent.
Are V and W independent?
No. Because the joint density contains a factor of √(v² - w²) in the denominator, it does not factor into a function of v times a function of w alone. Moreover, V > |W| must be satisfied for the density to be nonzero. These two variables are tightly coupled.
Potential Follow-up Questions
How do we interpret the domain constraints |w| ≤ v?
In order for x = (v + w)/2 and y = (v - w)/2 to be valid as nonnegative quantities (since x and y are squares of normals), we need v + w ≥ 0 and v - w ≥ 0. This condition translates to -v ≤ w ≤ v. Hence whenever we do the transformation to V and W, we must remember this domain restriction.
Why does each of Z₁² and Z₂² follow a gamma(½, 1) distribution?
Zᵢ², where Zᵢ is standard normal, is a classic example of a chi-square distribution with 1 degree of freedom, which is a special case of the gamma distribution with shape ½ and scale 2 if one uses the “rate vs. scale” parameterization carefully. In the more standard parameterization with scale 1 (not 2), we get x^( -1/2 ) e^(-x/2) up to a constant factor. This is consistent with the known relationship between the chi-square(1) distribution and the gamma distribution.
Can we confirm the normalization of this joint PDF?
One could integrate fᵥ,𝑤(v,w) over v from 0 to ∞ and w from -v to v. A convenient approach is to revert to x, y ≥ 0 in polar-like coordinates or to compute the integral by carefully handling the transformation. The result should come out to 1, confirming this is a valid probability density function.
How would we simulate random samples of (V, W) in practice?
Draw independent Z₁, Z₂ ~ Normal(0,1).
Compute V = Z₁² + Z₂².
Compute W = Z₁² - Z₂².
If you collect a large number of these (V, W) pairs, their empirical distribution will approximate fᵥ,𝑤(v,w).
What if we wanted the marginal distribution of W alone?
We could integrate out V over the allowable region |w| ≤ v < ∞. That is:
∫ from v=|w| to ∞ fᵥ,𝑤(v,w) dv.
It is less common to look only at W, but it can be done by this integration. The resulting distribution is related to a difference of gamma(½, 1) variables in a certain sense (though not in the usual “X - Y” because each variable is restricted to be ≥ 0 in its original domain).
This question often arises in advanced probability or transformations of random variables and is a typical test of one’s ability to handle non-linear transformations with domain restrictions.
Below are additional follow-up questions
What is the correlation between V and W, and how do we compute it?
To investigate the correlation, we first need E[V], E[W], and E[VW]. Recall:
V = Z₁² + Z₂²
W = Z₁² - Z₂²
Because Z₁ and Z₂ are i.i.d. standard normals, we know E[Zᵢ²] = 1 for i=1,2. Hence,
E[V] = E[Z₁²] + E[Z₂²] = 1 + 1 = 2, E[W] = E[Z₁²] - E[Z₂²] = 1 - 1 = 0.
Next, consider VW = (Z₁² + Z₂²)(Z₁² - Z₂²) = Z₁⁴ - Z₂⁴. We now need E[Z₁⁴] and E[Z₂⁴]. For a standard normal random variable Z, E[Z⁴] = 3. Therefore,
E[Z₁⁴ - Z₂⁴] = E[Z₁⁴] - E[Z₂⁴] = 3 - 3 = 0.
Thus E[VW] = 0. We already have E[V] = 2 and E[W] = 0. Consequently,
Cov(V, W) = E[VW] - E[V]E[W] = 0 - (2)(0) = 0.
Because their covariance is zero, Corr(V, W) = 0 / [√(Var(V)Var(W))], which gives Corr(V, W) = 0. A zero correlation, however, does not imply independence. Indeed, as we know, V and W are not independent.
Could W be positive or negative, and what does that tell us about the shape of its distribution?
Yes. W can be either positive or negative, since W = Z₁² - Z₂². If Z₁² happens to be larger than Z₂², W is positive, and otherwise it is negative. In fact, for given V = v, W can range from -v to +v. This indicates that the support of W is unbounded in principle, except that W is constrained to lie between -V and +V once we condition on V. This dependence in the domain underscores the fact that V and W cannot be independent. From a shape perspective, small absolute values of W occur more frequently because Z₁² and Z₂² are both “typically” close to 1 (on average), but large values of |W| are less probable, requiring a big discrepancy between Z₁² and Z₂².
How do we compute the moment generating function (MGF) or characteristic function of (V, W)?
To find the joint MGF M(t₁, t₂) = E[e^(t₁V + t₂W)], one approach would be to revert to x = Z₁² and y = Z₂², and write:
t₁V + t₂W = t₁(x + y) + t₂(x - y) = (t₁ + t₂)x + (t₁ - t₂)y.
Then M(t₁, t₂) = E[e^((t₁ + t₂)x + (t₁ - t₂)y)]. Since x and y are independent gamma(½, 1) variables, we factorize:
M(t₁, t₂) = E[e^((t₁ + t₂)x)] E[e^((t₁ - t₂)y)].
We thus need the MGF of a gamma(½,1) distribution. For a gamma(shape = α, scale = θ), the MGF is (1 - θt)^(-α) for t < 1/θ. In our case α = ½ and θ = 1, so
E[e^(tx)] = (1 - t)^(-1/2), valid for t < 1.
Hence,
M(t₁, t₂) = (1 - (t₁ + t₂))^(-1/2) * (1 - (t₁ - t₂))^(-1/2),
valid where both (t₁ + t₂) and (t₁ - t₂) are less than 1. A similar process works for the characteristic function by replacing t with i t (where i is the imaginary unit).
What happens if Z₁ and Z₂ are not independent, or not identically distributed?
The derivation we used heavily relies on the independence (which implies factorization of densities) and on each being standard normal (same scale, zero mean). If Z₁ and Z₂ are correlated normals with correlation ρ ≠ 0, then Z₁² and Z₂² are no longer independent, and the transformation to V and W becomes more complicated. In that case:
The distribution of x = Z₁² and y = Z₂² is no longer the product of two gamma(½,1) densities.
The region transformations might still hold, but the resulting joint PDF for (V, W) would pick up correlation terms in the exponent.
The domain constraints remain the same for x and y to be nonnegative, but the independence-based simplifications fail.
Similarly, if Z₁ and Z₂ have different variances, say σ₁² and σ₂², then x = Z₁²/σ₁² has a gamma(½, scale=σ₁²) distribution, and the entire result changes accordingly.
How can we interpret (V, W) in a geometric or real-world sense?
Geometrically, V = Z₁² + Z₂² is the squared radius in 2D space when we regard (Z₁, Z₂) as a random point in the plane. W = Z₁² - Z₂² measures the difference in squares of the two coordinates. If you imagine a sample of (Z₁, Z₂), points closer to the line Z₁² = Z₂² lead to smaller absolute values of W, while points lying near the axes in an extreme manner yield large |W|. This interpretation is sometimes encountered in signal processing where Z₁, Z₂ might be noise samples, or in dimension-reduction contexts where squared distances matter.
Could we directly simulate V and W without first simulating Z₁ and Z₂?
To generate a single sample (V, W) from the exact joint distribution, one would need a known method that draws from the joint f(V, W) = 1/(4π√(v² - w²)) exp(-v/2), subject to v ≥ 0 and |w| ≤ v. In practice, sampling Z₁, Z₂ ~ Normal(0,1) and then computing V, W is far simpler and aligns with standard libraries that generate normal deviates. Attempting to directly accept-reject for V, W might be more complicated: you would propose (v,w) in the valid region and check the acceptance probability proportional to exp(-v/2)/√(v² - w²). It is feasible, but often slower and more prone to numerical difficulties.
What are potential numerical stability issues when evaluating the joint PDF?
When you compute the expression:
1 / (4π√(v² - w²)) * exp(-v/2),
two potential numerical difficulties arise:
The term √(v² - w²) can be very small if |w| is close to v, causing potential division by a near-zero value. In floating-point arithmetic, this can lead to overflow in the PDF.
The exponential factor exp(-v/2) can underflow for large v.
In many practical applications, one might prefer working with the log of the PDF, log f(V, W) = -log(4π) - (1/2)log(v² - w²) - v/2, to maintain better numerical stability. Implementations in software libraries typically rely on stable “log-sum-exp” style calculations to avoid direct evaluation of exponentials.
How do we find the distribution of the ratio T = W / V?
Sometimes one wants to consider T = (Z₁² - Z₂²) / (Z₁² + Z₂²). This ratio measures how asymmetrically distributed the squares of Z₁ and Z₂ are, relative to their sum. To find the PDF of T alone:
We note T ∈ [-1, 1].
We can write W = T V and hence x = (v + tv)/2, y = (v - tv)/2.
One approach is to consider the transformation (V, T) from (x, y). Then integrate out V to get the marginal distribution of T.
This leads to nontrivial integrals but can be worked out. The final shape of T is reminiscent of a distribution that is heavily concentrated near ±1 only when one variable is close to zero while the other is large. The exact closed-form expression is more involved, but it highlights again the coupling between V and W.
What if we applied these distributions in a high-dimensional setting?
In higher dimensions, we could generalize:
Let Z = (Z₁, Z₂, ..., Zₙ) be a vector of i.i.d. standard normal variables.
Define V = ∑ Zᵢ² (the sum of squares, which is chi-square(n)).
Define a “difference” statistic in some manner, such as W = Z₁² - ∑ Zᵢ² (i≥2).
The question arises whether these transformations remain tractable. Typically, for dimension > 2, the geometry gets more intricate. The random variable V remains chi-square with n degrees of freedom, but any difference-based W that is not symmetrical might end up with complicated dependencies. In real-world ML tasks (like data augmentation or certain kernel methods), we often only rely on the properties of ∥Z∥² = ∑ Zᵢ² rather than differences among their squares, highlighting how specialized the 2D difference case is.