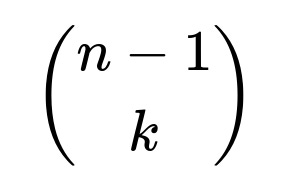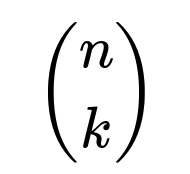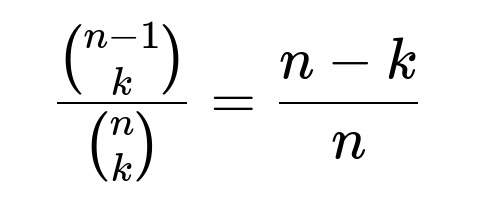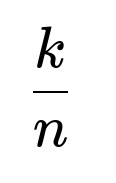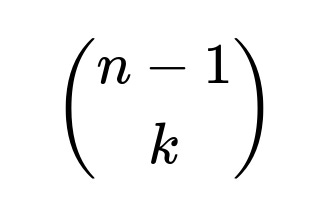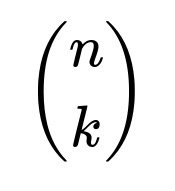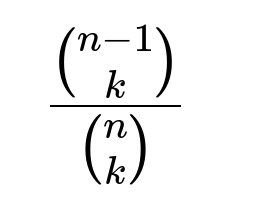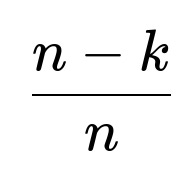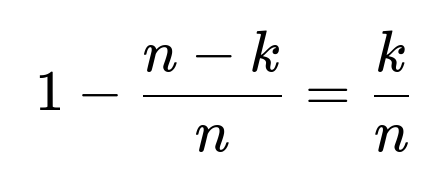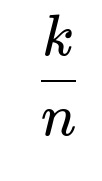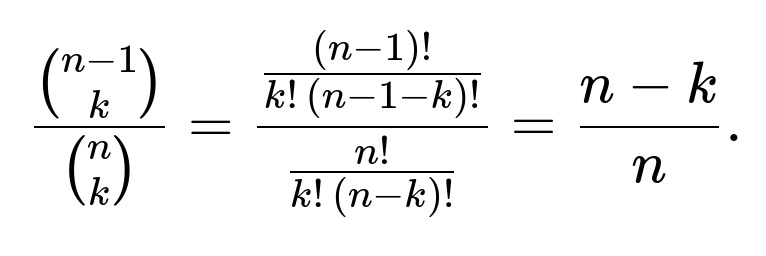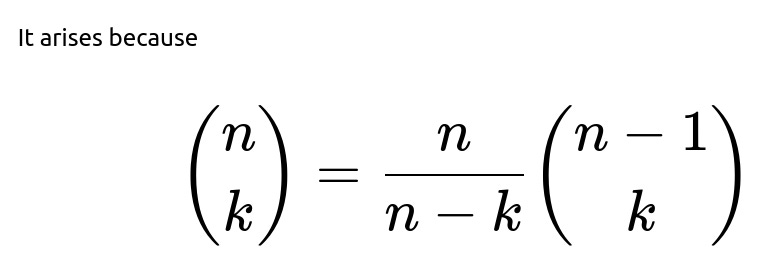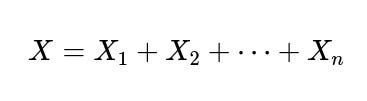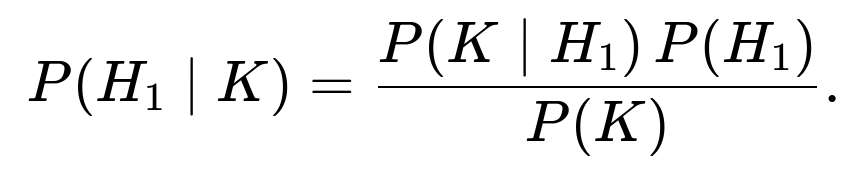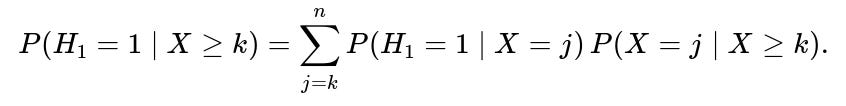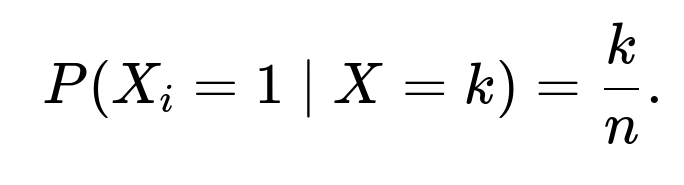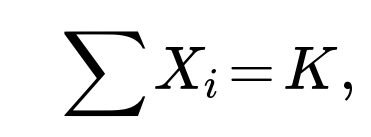ML Interview Q Series: Deriving the k/n Probability for First Head Given k Total Heads via Symmetry.
Browse all the Probability Interview Questions here.
A fair coin is flipped n times. It is observed that exactly k of those flips landed on heads. Under these conditions, what is the probability that the first flip was a head?
Short Compact solution
One way to see this is to count how many ways the first flip can be tails while still producing k heads in total. There are
ways to place the k heads among the remaining n - 1 flips if the very first flip is tails. Meanwhile, the total number of ways to have exactly k heads in n flips is
Hence, the probability that the first flip is tails (given k heads in total) is
. Subtracting from 1 shows that the probability the first flip is heads is
Comprehensive Explanation
The question is about conditional probability. We know we ended up with k heads in n total flips, and we want the probability that the very first flip was one of those heads. A fair coin implies that any arrangement of heads and tails with exactly k heads is equally likely.
Counting Possible Outcomes
Think about the set of all flip sequences that have exactly k heads. Each sequence is equally likely once we know there are k heads in total. We want to check, among those sequences, how many start with a head versus how many start with a tail.
If the first flip is tails, then the remaining n - 1 flips must contain all k heads. That leads us to
equally likely ways to distribute k heads among those n - 1 flips.
On the other hand, the total number of sequences with exactly k heads in n flips (no matter where those heads appear) is
. Dividing gives the probability that the first flip was tails:
. A direct combinatorial identity simplifies that ratio to
. Therefore, the probability that the first flip is heads is
Alternative Intuitive Explanation
Another way to interpret it is that if there are k heads in total out of n flips, then by symmetry each of the n positions is “equally likely” to be one of the k heads. Since the first position is just one among those n positions, the probability it is a head is
. This argument relies on the idea that all arrangements are equally probable once we know there are k heads total.
A Brief Numerical Example
If n = 5 and k = 2, then among all sequences of length 5 with exactly 2 heads, each such sequence is equally likely. We can list them (there are 10 in total), and exactly 2 out of 5 flips are heads in each sequence. Counting how many start with a head reveals it is 2/5 of all valid sequences. This simple example matches the formula k/n.
Follow-up question: Why exactly does the ratio of binomial coefficients simplify to (n - k) / n?
The key combinatorial identity is:
. You can derive it by explicitly writing out factorials or by a combinatorial argument that you can choose any particular position (like the first flip) in the sequence.
Once we know that ratio corresponds to the event “first flip is tails,” subtracting it from 1 gives the probability that the first flip is heads, which is k / n.
Follow-up question: Is there a direct exchangeability or symmetry argument behind k/n?
Yes. Consider the total n flips. If we do not yet know which positions are heads and which are tails, but we are told there are k heads in total, then any specific position (like the first flip) has an equal chance to be any of the k heads among the n positions. Thus that position has probability k/n of being a head. This reasoning is a classic example of exchangeability: all n flips are indistinguishable from one another aside from their positions, and no prior bias is given that would favor the first position over the others.
Follow-up question: What if the coin is not fair? Does the same formula still hold?
If the coin is biased with probability p of landing heads, then the probability of having k heads in n flips is different. Once we condition on observing exactly k heads, the distribution of heads among the n positions is no longer uniform if p ≠ 0.5. However, there is still an exchangeability principle for Bernoulli trials. Given exactly k successes in n trials with identical success probability p, every arrangement of k heads and n - k tails has the same prior probability. As a result, each arrangement with k heads is still equally likely, so any specific position (like the first flip) will be a head in k out of n equally likely configurations. Even in the biased case, the conditional probability that the first flip is heads—knowing we have exactly k heads total—remains k/n.
This might seem counterintuitive, but it is a direct consequence of each arrangement with exactly k heads being equally probable once you have the condition “there are k heads total.” The coin’s bias affects how likely it is that k heads occur overall, but once that is known, it does not affect how those k heads are arranged across the n positions.
Follow-up question: How can we verify or simulate this result in practice, for example in Python?
We can write a quick simulation that repeats many trials, counts how often we get k heads out of n flips, and then among those trials, checks how often the first flip was heads.
import numpy as np
def simulate_first_toss_probability(n, k, p=0.5, trials=1_000_000):
count_first_heads = 0
count_k_heads_and_first_heads = 0
for _ in range(trials):
flips = np.random.rand(n) < p # True for heads, False for tails
total_heads = np.sum(flips)
if total_heads == k:
if flips[0]:
count_k_heads_and_first_heads += 1
count_first_heads += 1
if count_first_heads == 0:
return 0.0
return count_k_heads_and_first_heads / count_first_heads
# Example usage:
n = 10
k = 3
approx_probability = simulate_first_toss_probability(n, k, p=0.5, trials=500000)
print("Approx probability that the first toss is heads given k heads in total:", approx_probability)
This code performs many simulated experiments of flipping a coin n times with probability p of heads. It filters to the experiments where exactly k heads are observed. Among those, it counts how many times the first flip is a head. Dividing these yields an empirical estimate of the conditional probability. When p = 0.5, you should see a result close to k/n.
Follow-up question: How does this reasoning relate to broader ideas in Machine Learning or Bayesian statistics?
In Bayesian terms, if we treat each flip as an i.i.d. Bernoulli trial with unknown probability p, then observing k heads in n flips updates our posterior for p. But if we specifically ask: “Given that we know there are k heads in n flips, what is the probability the first flip was head?” the result does not actually require knowledge of p, because the question is purely about how those k heads are distributed among positions, not about the chance of flipping heads in general. This can be seen as a manifestation of the fact that, conditioned on k heads total, each arrangement of heads is equally likely (the posterior for how heads are allocated among positions is uniform over all combinations). Therefore, each of the n flips is equally likely to be one of the k heads.
Follow-up question: Are there any edge cases or corner scenarios worth highlighting?
One boundary situation is k = 0 or k = n. If k = 0, then all flips are tails, so the probability that the first flip is heads is 0. The formula k/n gives 0/n = 0. Similarly, if k = n, all flips are heads, so the probability that the first flip is heads is 1, matching the formula k/n = n/n = 1. These edge cases confirm that the expression works in extreme conditions. Another subtle point is that you need at least one valid arrangement for the condition “k heads in n flips” to make sense. If k is outside the range [0, n], that event cannot occur, and the conditional probability is undefined.
Below are additional follow-up questions
Follow-up question: How does using indicator random variables help us verify that the probability of the first flip being heads (given exactly k heads in total) is k/n?
One way to analyze this problem is to introduce an indicator random variable for each position. Let’s say we define:
Xᵢ = 1 if the i-th flip is heads, and 0 otherwise, for i = 1, 2, …, n.
We know that
is the total number of heads in n flips. The condition that there are exactly k heads translates to X = k. Now consider X₁ alone:
We want P(X₁ = 1 | X = k), meaning the probability that the first flip is heads given k heads in total.
By exchangeability (the fact that each flip is under identical conditions), E(X₁ | X = k) is the same as the fraction k/n. Another way to see it is via linearity of expectation: the sum of the conditional expectations of each indicator given X = k must equal k. If each indicator is equally likely to be 1 under that condition, each must have an expectation of k/n. That in turn implies P(X₁ = 1 | X = k) = k/n.
Potential Pitfalls and Edge Cases
One might confuse unconditional expectation E(X₁) with the conditional expectation E(X₁ | X = k). The unconditional expectation for X₁ would be 1/2 for a fair coin, but once we know there are k heads in total, the condition changes the distribution.
If k = 0 or k = n, then the first indicator either must be 0 or must be 1 respectively, which is consistent with the formula k/n = 0 or 1.
If we tried to use indicator variables but forgot the conditioning, we would not arrive at the correct conditional probability.
Follow-up question: If the probability of heads changes over time (e.g., the coin is not identically distributed), does k/n still hold?
When each flip does not have the same probability of landing heads, the scenario is no longer “exchangeable.” Specifically, if we denote pᵢ as the probability that the i-th flip is heads, then once you know there are k heads in total, the flips are not all equally likely to occupy the k head-positions. Some flips may have had a higher chance of being heads than others. As a result, the probability that the first flip is a head, conditioned on k heads in total, depends on p₁, p₂, …, pₙ. In general, the simple result k/n does not hold.
Potential Pitfalls and Edge Cases
If p₁ is much larger than the other pᵢ, the first position is more likely to be among the k heads. The conditional probability would exceed k/n.
If p₁ is much smaller than the other pᵢ, it might be less likely to be among the k heads, so the probability would drop below k/n.
Some might try to apply the combinatorial argument directly, but that presupposes every arrangement with k heads is equally likely. That assumption only holds when p₁ = p₂ = … = pₙ.
Follow-up question: Could we directly apply Bayes’ theorem to derive the probability that the first flip was heads, given that k out of n flips are heads?
Yes. You can frame the event “first flip is heads” as H₁ and “there are k heads total” as K. Then Bayes’ theorem tells us:
For a fair coin:
P(H₁) = 1/2.
P(K) = (1/2)ⁿ × C(n, k) if we are looking at the unconditional event of k heads in n flips.
P(K | H₁) is the probability that there are k heads total, given that the first flip is heads. This would be (1/2)ⁿ × C(n-1, k-1), because if the first flip is already heads, you only need k-1 additional heads among the remaining n-1 flips.
Putting it all together:
P(H₁ | K) = [((1/2)ⁿ × (n-1 choose k-1)) × (1/2)] / [(1/2)ⁿ × (n choose k)] = ( (n-1 choose k-1) ) / [2 × (n choose k)].
And the binomial coefficient identity is:
(n choose k) = (n-1 choose k-1) + (n-1 choose k).
to confirm it simplifies exactly to k/n.
Potential Pitfalls and Edge Cases
Omitting the factor 1/2 for P(H₁) or mixing up the unconditional versus conditional probabilities can lead to mistakes.
For k=0, P(H₁ | K) = 0 trivially. For k=n, P(H₁ | K) = 1. These match the expected extremes.
If the coin is not fair but still has constant bias p, the expressions for P(K), P(K | H₁), and P(H₁) would change. However, once again the ratio would come out to k/n due to each sequence with k heads being equally likely under the condition that exactly k heads occurred.
Follow-up question: What if we only know that “k or more heads” occurred instead of “exactly k heads”? Would the probability for the first flip being heads still be k/n?
If we condition on the event “k or more heads,” the distribution among the possible numbers of heads from k to n changes. We can write that event as X ≥ k. Within that event, there could be multiple sub-events: X = k, X = k+1, …, X = n. The probability that the first flip is heads in that broader condition is not simply k/n. You would need to account for how likely it is that there are exactly k heads, exactly k+1 heads, etc., and weigh each scenario appropriately.
Mathematically, you would compute:
Given that for each j, P(H₁ = 1 | X = j) = j/n, you still have to average those fractions j/n with weights P(X = j | X ≥ k). Those conditional probabilities depend on the distribution of X. In the fair coin case, you might get a fraction that does not simply reduce to k/n.
Potential Pitfalls and Edge Cases
Overlooking the fact that “k or more heads” lumps together multiple scenarios, each with different probabilities of the first flip being heads.
If k = n, that means “n or more heads,” which is equivalent to “exactly n heads,” and so the probability is 1. Otherwise, there’s a blend of probabilities from k/n, (k+1)/n, (k+2)/n, etc.
Follow-up question: What if the total number of flips n is itself random? Does the argument for k/n remain valid?
When n is random, the combinatorial argument changes because we do not have a fixed-length sequence. You would have to condition on the event “we ended up with exactly k heads and the number of flips was n.” If you fix n after the fact (i.e., you know that we definitely observed n flips in total, with k heads), then the same combinatorial argument that yields k/n still applies. However, if n is random and unobserved, or partially known, you have a more complicated scenario involving the joint distribution of (n, k).
Potential Pitfalls and Edge Cases
If we only know “there were k heads by the time we stopped,” but the stopping rule depends on whether heads appear, the sample is biased. For example, if we stop flipping once we see a certain number of heads, that changes the distribution of how heads occur in the timeline.
If n is decided externally but not known to us, we must carefully incorporate the distribution for n into the analysis before drawing conclusions about the probability of the first flip being heads.
Follow-up question: How does this reasoning extend to the probability that the i-th flip (for any i) was heads, given that there are k heads total?
By symmetry, each flip i = 1, 2, …, n is in an identical position once we only know the total k but nothing else about the positions of those heads. Thus:
It is not just for the first flip; it also holds for the second, third, or any i-th flip. This is a direct byproduct of exchangeability in Bernoulli trials with identical probability of heads.
Potential Pitfalls and Edge Cases
If someone mistakenly focuses only on the first flip’s probability, they might forget that the same logic extends to every flip. The entire argument does not break if we shift to the second or last flip.
If flips are not i.i.d. (for instance, the coin might be fair but some external factor influences flip outcomes), the position-based symmetry can be broken, invalidating the k/n result for an arbitrary position.
Follow-up question: Could there be a continuous analog of this concept, for example, in a scenario where we have an integral measure of successes rather than a discrete count?
In some statistical or machine learning contexts, you might deal with a continuous analog of “heads or tails” (like success/failure) that is generalized to real-valued outcomes. However, once we lose the purely discrete nature of heads/tails, we cannot directly talk about “exactly k heads.” We might talk about “the sum of outcomes is k,” but then exchangeability has to be reformulated. For instance, if we have X₁, X₂, …, Xₙ i.i.d. continuous random variables, and we condition on the sum
it can be more involved to figure out the distribution of each Xᵢ. In many well-known cases (e.g., i.i.d. Gamma variables), it is possible to show that the distribution of each Xᵢ conditioned on the sum is the same. However, the ratio k/n concept is specifically tied to counting discrete events.
Potential Pitfalls and Edge Cases
Attempting to directly extend “k heads out of n flips” to a continuous setting can cause confusion. The entire combinatorial argument no longer applies if we do not have discrete states to choose from.
In the continuous scenario, one has to rely on the joint density and consider properties of conditional distributions. For example, in the Dirichlet distribution world, if each Xᵢ is a Beta random variable, or if we look at sums of i.i.d. exponentials, we get different but related kinds of “exchangeability.”