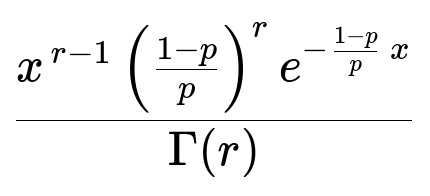ML Interview Q Series: Deriving the Negative Binomial Distribution from a Gamma-Poisson Mixture
Browse all the Probability Interview Questions here.
You simulate a random observation from the random variable (X) with the gamma density
where (r) and (p) are given positive numbers. Then you generate an integer by taking a random observation from a Poisson distribution whose expected value is given by the number you have simulated from the gamma density. Let (N) denote the generated integer. What is the probability mass function of (N)?
Short Compact solution
By the law of conditional probability (treating (X) as the parameter of a Poisson distribution), we have:
(P(N=k)) = (\displaystyle \int_{0}^{\infty} \bigl(e^{-x},x^{k}/k!\bigr),\bigl(\tfrac{1-p}{p}\bigr)^{r},\frac{x^{r-1},e^{-\tfrac{1-p}{p}x}}{\Gamma(r)} ,dx).
Using properties of the gamma density and performing the integral, we obtain:
for (k = 0, 1, 2, \dots). This corresponds to a negative binomial distribution with parameters (r) and (p), where (r) need not be an integer.
Comprehensive Explanation
Mixture of Gamma and Poisson Distributions We start by recognizing that (N \mid X = x) follows a Poisson(x) distribution. Thus,
The conditional probability mass function of (N), given (X = x), is: P(N = k | X = x) = e^(-x) x^k / k!.
The random variable (X) itself follows a gamma distribution with shape parameter (r) and rate ((1-p)/p). Explicitly, its probability density function (pdf) is: f_X(x) = [((1-p)/p)^r / Gamma(r)] x^(r - 1) e^(-((1-p)/p) x), for x > 0.
To find the unconditional distribution of (N), we use the law of total probability by integrating out (X). That is: P(N = k) = ∫[ P(N = k | X = x) f_X(x) ] dx.
Carrying Out the Integral Substitute each piece into the integral:
P(N = k | X = x) = e^(-x) x^k / k!.
f_X(x) = [((1-p)/p)^r / Gamma(r)] x^(r - 1) e^(-((1-p)/p) x).
So we get: P(N = k) = ∫[ (e^(-x) x^k / k!) * (((1-p)/p)^r / Gamma(r)) * x^(r - 1) e^(-((1-p)/p) x ) ] dx, where the integration is from 0 to ∞.
Combine the exponents and factors of x:
e^(-x) e^(-((1-p)/p) x) = e^(-[1 + (1-p)/p] x) = e^(-[ (p + (1-p)) / p ] x) = e^(-x/p).
x^k x^(r-1) = x^(k + r - 1).
Collect constants: 1/k!, ((1-p)/p)^r, and 1/Gamma(r).
Hence: P(N = k) = [((1-p)/p)^r / (k! Gamma(r)) ] ∫[ x^(k + r - 1) e^(-x/p) ] dx.
Inside the integral, if we treat p as the scale (not the rate), we can rewrite e^(-x/p) as e^(-(1/p) x). Recall that the gamma pdf with shape parameter (r + k) and scale p has the integral form: ∫[ (1 / (Gamma(r+k) p^(r+k)) ) x^( (r + k) - 1 ) e^(-x / p ) ] dx = 1.
Careful rearrangement shows that, effectively, we are integrating exactly the kernel of a gamma((r + k), p) distribution. The result of the integral then simplifies to:
P(N = k) = (Gamma(r + k) / [k! Gamma(r)]) p^k (1-p)^r.
Negative Binomial Distribution This final form is recognized as the probability mass function of a negative binomial random variable with shape parameter r (not necessarily an integer) and “success probability” p. There are multiple parameterizations of the negative binomial distribution in different texts, but a common one is:
This generalizes the idea of waiting for r “successes” (with success probability p) in a sequence of Bernoulli trials when r is a positive real number rather than necessarily an integer. In many references, this distribution is also referred to as the Pólya distribution or a gamma–Poisson mixture.
Potential Follow-Up Question 1
What happens if r is an integer? How does that relate to the classical interpretation of the negative binomial distribution?
If r is an integer, say r = m for some positive integer m, then the gamma distribution for X simplifies to the Erlang distribution. In that case, the resulting negative binomial distribution has the classical interpretation of “the number of failures before the m-th success” in a sequence of Bernoulli trials with success probability p. Specifically, you could interpret N as the total number of failures (k) that occur by the time you achieve m successes.
However, when r is not necessarily an integer, the mixture construction still yields a valid discrete distribution, yet it loses that strict “number of failures until r-th success” combinatorial interpretation. Instead, one can interpret it purely through the gamma-Poisson mixture mechanism.
Potential Follow-Up Question 2
Why is the gamma distribution a natural choice for the prior over the Poisson mean in a Bayesian or mixture context?
The gamma distribution is a conjugate prior for the Poisson distribution’s rate parameter. In Bayesian statistics:
If λ ~ Gamma(α, β) and conditioned on λ you have y ~ Poisson(λ), then the posterior distribution for λ given the observation y is also gamma: Gamma(α + y, β + 1).
Conjugacy simplifies computations and leads to closed-form expressions for predictive distributions. In a frequentist mixture context, mixing a Poisson(λ) with a gamma prior for λ leads to the negative binomial distribution as the marginal distribution of y, exactly as we derived. This makes the gamma–Poisson mixture a common and convenient model for count data exhibiting overdispersion relative to the Poisson model. Overdispersion arises when the variance of the counts exceeds the mean, something that the plain Poisson cannot account for. The gamma–Poisson (negative binomial) mixture explicitly introduces additional variability in the Poisson rate parameter through the gamma distribution, increasing the variance in the marginal distribution of N.
Below are additional follow-up questions
Follow-Up Question 1
What is the moment generating function (MGF) of the negative binomial distribution in the gamma–Poisson mixture form, and how do you derive it?
When dealing with the negative binomial distribution arising from a gamma–Poisson mixture, we can derive its MGF by leveraging the fact that the moment generating function of a Poisson random variable with random mean X can be computed by taking the expectation over the distribution of X.
For a random variable N that is conditional on X ~ Gamma(r, (1-p)/p) to be Poisson with mean X, the MGF of N is:
M(t) = E[ exp(tN) ] = E[ E( exp(tN) | X ) ].
Because N|X=x is Poisson(x), the conditional MGF of N given X=x is exp( x(e^t - 1) ). Hence,
M(t) = E[ exp( X(e^t - 1) ) ].
We then use the MGF of X when X is gamma-distributed. If X is gamma(r, (1-p)/p) (with shape r and rate (1-p)/p), its MGF is ( ( (1-p)/p ) / ( (1-p)/p - (e^t - 1) ) )^r for values of t such that the expression is well-defined. Simplifying, we eventually get an MGF of the form consistent with the negative binomial distribution:
M(t) = ( (1-p) / (1 - p e^t) )^r,
provided that p e^t < 1 (to ensure convergence). This shows how the mixture directly yields a known closed-form MGF for the negative binomial.
A subtle point is ensuring the range of t values where this MGF is finite, especially if e^t is large. In practical computation, numerical stability can be a challenge if t > 0 is large, leading to very large e^t. Another pitfall is mixing up rate vs. scale parameterization for the gamma; the MGF form depends on whether you used a rate parameter (which is (1-p)/p in the question) or a scale parameter p/(1-p).
Follow-Up Question 2
How does the parameterization using r and p compare with other common parameterizations of the negative binomial (for instance, using a mean parameter or a dispersion parameter)?
Many texts give alternative formulations of the negative binomial distribution. For example, one might see a parameterization using (r, μ) where μ is the mean of the distribution, or (r, θ), where θ might be the success-failure odds. In the context of the gamma–Poisson mixture:
The “number of failures until r successes” parameterization often writes the PMF as a function of r (the number of successes) and p (the success probability in each Bernoulli trial).
Another parameterization focuses on the mean and dispersion. The mean of the negative binomial in the (r, p) form is (r p) / (1 - p), and the variance is (r p) / (1 - p)^2. This is sometimes more convenient when modeling count data with a known mean-variance relationship.
A subtlety arises if you see references that define the gamma distribution with a shape α and scale β rather than a rate parameter. Keeping track of which parameterization is used is crucial to avoid confusion in formulas. A typical pitfall is forgetting that the scale parameter is the inverse of the rate parameter, which can cause misidentification of the mixture.
Follow-Up Question 3
What happens if p is very close to 1 or very close to 0, and how does this affect the distribution of N?
If p → 1, then (1-p) → 0. This typically means the gamma distribution for X is centered around a smaller and smaller value (since the rate (1-p)/p → 0, implying the mean of X remains finite but the shape shifts). In the limit, N is more likely to be close to 0 because the underlying Poisson mean tends to be quite small. The distribution becomes heavily concentrated around lower counts.
If p → 0, the term (1-p)/p becomes large, so the mean of the gamma distribution for X also grows. Hence the Poisson mean X is large on average, and N tends to assume large values. The negative binomial’s probability mass shifts toward higher counts, sometimes with a long right tail.
A pitfall in real-world data modeling is not properly checking if p is estimated to be extremely close to 0 or 1, which might indicate the model is degenerate or that the data do not suit a negative binomial approach well. Numerical instability can also arise in software implementations when p is near boundary values.
Follow-Up Question 4
How does the scale vs. rate parameterization of the gamma distribution affect the Poisson mixture, and how do you avoid confusion?
In the question, the gamma density is expressed in a rate form with parameter (1-p)/p. However, many statistical software libraries and texts use a scale parameterization where the gamma pdf is written as:
( 1 / ( Γ(r) θ^r ) ) x^(r-1) e^(- x / θ ),
where θ is the scale. The relationship between scale and rate (often denoted β or λ) is:
scale = 1 / rate.
This difference directly affects how we interpret the mixture:
If X ~ Gamma(r, rate=(1-p)/p), then the mean of X is r * [1 / ((1-p)/p)] = r p / (1-p).
If X ~ Gamma(r, scale=p/(1-p)), then the mean of X is r * p/(1-p).
They yield the same distribution but require careful conversion. A common pitfall is mixing up these parameterizations and ending up with inconsistent results for the mixture distribution or the negative binomial’s PMF. Always double-check the documentation or function signature in software libraries like NumPy or PyTorch to confirm which parameterization (rate vs. scale) is being used.
Follow-Up Question 5
What are the key differences between a standard negative binomial distribution and a zero-inflated negative binomial distribution, and under what real-world situations would you prefer one over the other?
A zero-inflated negative binomial (ZINB) model adds an additional component for “excess zeros.” Specifically, the model assumes:
With probability ψ (the zero-inflation parameter), the random variable is deterministically 0.
With probability (1 - ψ), the random variable is drawn from a negative binomial distribution.
Real-world datasets often have more zeros than can be accounted for by a standard count model (like Poisson or negative binomial). Zero-inflated models attempt to capture the process that, for some portion of observations, a zero outcome is inevitable (e.g., in medical data, certain patients never contract a disease at all because they’re in a zero-risk category), whereas others follow the usual count distribution.
Pitfalls and edge cases include:
Overfitting the zero-inflation parameter when data do not truly have a structural zero mechanism (leading to false inflation of zero outcomes).
Underestimating the probability of zero if data are “hurdle-like” (i.e., a process that must exceed a threshold to generate non-zero counts).
Fitting complexities: zero-inflated models can sometimes be sensitive to initialization methods and can produce boundary estimates if the data are extremely zero-heavy.
Follow-Up Question 6
In practice, when would you use a negative binomial distribution instead of a Poisson distribution?
The negative binomial model is often chosen when the data exhibit overdispersion relative to a Poisson assumption. In a Poisson distribution, the mean = variance. However, for many real-world datasets (e.g., insurance claim counts, word frequencies in text, web traffic, etc.), the variance exceeds the mean. If you were to fit a Poisson model, you would observe that the Poisson underestimates the probability of observations far from its mean and fails to capture the extra variability.
Common real-world considerations:
If your residuals from a Poisson regression show overdispersion, switching to a negative binomial regression often gives a better fit.
In the presence of large outliers, the negative binomial’s heavier tail accommodates big counts more gracefully.
A subtle pitfall is that sometimes zero-inflation or other data structures (like hurdle models) might be the cause of apparent overdispersion, so negative binomial alone might not fully solve the mismatch if there is an excess zeros phenomenon.
Follow-Up Question 7
How might you incorporate additional predictors (covariates) into a negative binomial model, analogous to how we have Poisson regression for count data?
You can create a negative binomial regression by linking the mean parameter μ = r p / (1-p) (or any alternative parameterization) to a linear predictor of covariates. For instance, we might set:
log( μ_i ) = β_0 + β_1 x_{i1} + ... + β_k x_{ik}.
Alternatively, some parameterizations let you keep r constant and let p (the success probability) vary as a function of covariates. For instance,
logit(p_i) = β_0 + β_1 x_{i1} + ... + β_k x_{ik}.
Either approach is viable, but it depends on how you want to interpret the regression coefficients and how the software packages define negative binomial regression. The edge cases here include ensuring that p_i remains between 0 and 1 (for the logistic link) and that the model does not degenerate for extreme predictor values. A common pitfall is incorrectly mixing up the link function for the negative binomial portion and ending up with invalid estimates (like negative means).
Moreover, in practice, you need to estimate both the dispersion parameter (analogous to r) and the regression coefficients. Some libraries treat r as a fixed overdispersion parameter, while others let it vary or be estimated. Properly diagnosing convergence issues is crucial, since negative binomial regression models can be more sensitive than Poisson regression to local optima or boundary solutions if the data are extreme.