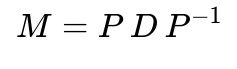ML Interview Q Series: Determine whether the following matrix can be diagonalized, and if so, demonstrate how to perform the diagonalization
📚 Browse the full ML Interview series here.
Comprehensive Explanation
To analyze whether a given square matrix is diagonalizable, the main steps involve finding its eigenvalues, corresponding eigenvectors, and checking if there is a complete set of linearly independent eigenvectors that spans the entire space. If the matrix has n linearly independent eigenvectors in n-dimensional space, then it can be diagonalized.
Below is the central formula that describes the diagonalization of a matrix M:
Where:
M is the original square matrix (n x n).
D is a diagonal matrix whose main diagonal entries are the eigenvalues of M.
P is the matrix composed of the n linearly independent eigenvectors of M as its columns.
P^{-1} is the inverse of P.
If M can be represented in the form M = P D P^{-1}, we say M is diagonalizable. However, if one cannot find a full set of n linearly independent eigenvectors, M is not diagonalizable.
Steps to Check for Diagonalizability
Find the characteristic polynomial of M. This typically involves calculating det(M - lambdaI) = 0 in order to solve for the eigenvalues (the values of lambda).
For each eigenvalue lambda_i, find the eigenvectors that satisfy (M - lambda_i I)v = 0. Each set of solutions for v forms the eigenspace corresponding to lambda_i.
Check the dimension of each eigenspace. If the sum of the dimensions of all eigenspaces equals n (assuming M is n x n), then we can choose a total of n linearly independent eigenvectors. This means M is diagonalizable.
Construct the matrix P by placing each of these n linearly independent eigenvectors as columns. Form the diagonal matrix D by placing the corresponding eigenvalues along its diagonal in the same order as the columns in P.
Finally, verify that M = P D P^{-1} is satisfied.
Key Observations
When an eigenvalue has algebraic multiplicity m, but its eigenspace has dimension less than m, we cannot collect enough linearly independent eigenvectors for that eigenvalue. This is often the reason a matrix fails to be diagonalizable.
Real matrices sometimes have complex eigenvalues, in which case diagonalization over the real field is not always possible unless we include complex numbers. However, if working over the complex field, it might still be diagonalizable.
Symmetric (or Hermitian in the complex case) matrices are guaranteed to be diagonalizable with an orthogonal (or unitary) P.
If the matrix is already in a form that shows the eigenvalues clearly (for example, block upper triangular with distinct diagonal entries), it is often simpler to see how it might be diagonalized.
Example of Diagonalization in Python
import numpy as np
# Suppose we have a matrix M
M = np.array([[2, 1],
[0, 2]], dtype=float)
# Step 1: Compute eigenvalues and eigenvectors
eigenvals, eigenvecs = np.linalg.eig(M)
# eigenvals is an array of eigenvalues
# eigenvecs is an array of eigenvectors as columns
# Step 2: Construct the diagonal matrix D from eigenvals
D = np.diag(eigenvals)
# Step 3: Form the matrix P from eigenvecs
P = eigenvecs
# Step 4: Compute P_inv
P_inv = np.linalg.inv(P)
# Let's verify M = P D P_inv
M_reconstructed = P @ D @ P_inv
# M_reconstructed should be close to M if diagonalization is correct
print("Original M:\n", M)
print("Reconstructed M from P D P_inv:\n", M_reconstructed)
print("Diagonal matrix D:\n", D)
print("Matrix P:\n", P)
print("Inverse of P:\n", P_inv)
In this example, if the matrix M can be fully diagonalized, the reconstruction M_reconstructed will match the original M (within numerical precision). However, if M is not diagonalizable (for instance, if it lacks a sufficient number of linearly independent eigenvectors), then numerical approaches might fail or the eigen-decomposition might reflect that certain eigenvectors do not span the entire space.
Potential Follow-Up Questions
What happens if the matrix has repeated eigenvalues?
When an eigenvalue is repeated, the algebraic multiplicity is larger than 1. We must check the dimension of the corresponding eigenspace. If the dimension of the eigenspace for this repeated eigenvalue equals its algebraic multiplicity, we will still obtain enough eigenvectors. If not, the matrix is not diagonalizable.
Is every diagonalizable matrix invertible?
A diagonalizable matrix can be invertible or non-invertible. If at least one eigenvalue is zero, the diagonal matrix D has a 0 on its diagonal, which makes the matrix singular (its determinant is 0), hence it is not invertible. So diagonalizable does not always imply invertible.
Why do symmetric matrices guarantee diagonalizability?
A real symmetric matrix (or a Hermitian matrix in the complex domain) is guaranteed to have a complete set of orthonormal eigenvectors. This is a fundamental result of real symmetric (or Hermitian) matrix theory. Hence, such matrices are always diagonalizable (in fact, orthogonally or unitarily diagonalizable).
How do we handle matrices that fail to have enough independent eigenvectors?
In that case, we cannot diagonalize them. One can still consider other decompositions such as the Jordan canonical form, which generalizes diagonalization by introducing Jordan blocks for cases where there are fewer eigenvectors than the size of the matrix.
Can a matrix be diagonalizable over the complex field but not over the real field?
Yes. Certain real matrices have complex eigenvalues (such as rotation matrices in 2D), meaning they do not have real eigenvalues or real eigenvectors. They can, however, be diagonalizable over the complex field if they have distinct complex eigenvalues and enough linearly independent eigenvectors in the complex domain.
How does numerical precision affect diagonalization in practice?
In real-world settings, floating-point precision may cause numerical instability, especially if eigenvalues are very close to each other or if the matrix is nearly defective (having repeated eigenvalues but almost insufficient eigenspace dimensions). Algorithms like the QR algorithm for eigen-decomposition can suffer from round-off errors, making it crucial to check the numerical stability and condition numbers.