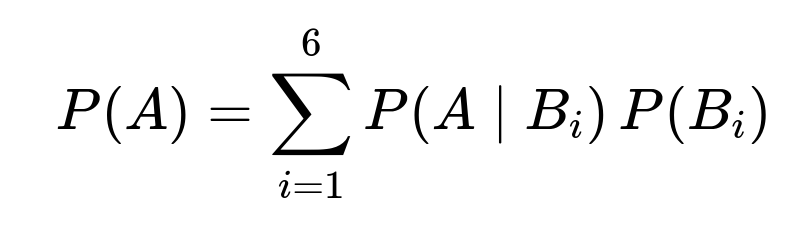ML Interview Q Series: Die-Roll Conditioned Ball Draws: Calculating Probabilities with Total Probability and Bayes' Theorem.
Browse all the Probability Interview Questions here.
A jar contains 5 blue balls and 5 red balls. You roll a fair die once. You then randomly draw (without replacement) as many balls from the jar as the number of points rolled on the die. (a) What is the probability that all of the balls drawn are blue? (b) What is the probability that the number of points shown by the die is r given that all of the balls drawn are blue?
Short Compact solution
Part (a)
Using the law of total probability:
where
A is the event that all drawn balls are blue,
B_i is the event that the die roll is i,
P(B_i)=1/6 for each i=1,...,6.
For i=1,...,5:
P(A|B_i) = (5 choose i)/(10 choose i).
For i=6:
P(A|B_6) = 0 (since you cannot draw 6 blue balls when there are only 5 available).
Hence,
P(A) = (1/6) * [ (5 choose 1)/(10 choose 1) + (5 choose 2)/(10 choose 2) + (5 choose 3)/(10 choose 3) + (5 choose 4)/(10 choose 4) + (5 choose 5)/(10 choose 5) ] = 5/36.
Part (b)
We want P(B_r | A). By definition:
Using P(A|B_r) = (5 choose r)/(10 choose r) for r=1,...,5 and zero for r=6, and P(B_r)=1/6, we get:
P(B_r | A) = [ (1/6) * (5 choose r)/(10 choose r ) ] / (5/36).
Numerically, for r=1,...,6, this yields:
r=1: 3/5
r=2: 4/15
r=3: 1/10
r=4: 1/35
r=5: 1/210
r=6: 0
Comprehensive Explanation
Overview of the problem setting
We have a jar with 5 blue and 5 red balls (10 total). We roll a fair six-sided die exactly once. If the outcome of the die is i, then we draw i balls from the jar (without replacement). We define:
A: Event that every drawn ball is blue.
B_i: Event that the die shows the value i.
Because the die is fair, each B_i occurs with probability 1/6. However, the probability of drawing only blue balls (event A) depends on how many balls i we draw.
Detailed derivation for Part (a)
Law of Total Probability We want P(A). By the law of total probability applied to the partition B_1,...,B_6:
Conditional Probability P(A | B_i)
If we roll i, we draw i balls. We want all of them to be blue.
The number of ways to choose i blue balls from the 5 blue available is (5 choose i).
The total number of ways to choose i balls from all 10 is (10 choose i).
Hence, P(A | B_i) = (5 choose i)/(10 choose i), provided i ≤ 5.
If i=6, it is impossible to draw 6 blue balls from only 5 available. So P(A | B_6)=0.
Combine with P(B_i) Since P(B_i)=1/6 for each i=1,...,6, we get:
P(A) = (1/6)*[ (5 choose 1)/(10 choose 1) + (5 choose 2)/(10 choose 2) + (5 choose 3)/(10 choose 3) + (5 choose 4)/(10 choose 4) + (5 choose 5)/(10 choose 5) ].
Final Summation Evaluating the above binomial coefficients yields 5/36.
Detailed derivation for Part (b)
We want P(B_r | A). This is the probability that the die roll was r given that all drawn balls are blue. We use Bayes’ rule:
Bayes’ Rule P(B_r | A) = P(A ∩ B_r)/P(A).
Compute P(A ∩ B_r)
P(A ∩ B_r) = P(A | B_r) * P(B_r).
We know P(A | B_r) = (5 choose r)/(10 choose r) for r=1,...,5 and 0 for r=6.
Also P(B_r)=1/6 for each r.
Division by P(A) Using P(A)=5/36, we get:
Numerical Values
For r=1: Substitute (5 choose 1)/(10 choose 1)=5/10=1/2, multiply by 1/6 => 1/12, then divide by 5/36 => 3/5.
For r=2: (5 choose 2)/(10 choose 2)=10/45=2/9, multiplied by 1/6 => 2/54=1/27, divided by 5/36 => 4/15.
Similarly for r=3, 4, 5, we get 1/10, 1/35, 1/210, and for r=6 it is 0.
Thus we have a clear distribution of P(B_r | A) across r=1,...,6.
Potential Follow-Up Questions
Why do we only sum up to i=5 in part (a)?
Because the probability of drawing 6 blue balls out of 5 available is zero. Therefore, P(A|B_6)=0 and it contributes nothing to the sum.
Are these events independent?
No. The event that all balls drawn are blue depends on how many balls we draw. Thus A and B_i are not independent events. The probability of A given B_i changes significantly based on i.
How does this relate to the hypergeometric distribution?
The probability P(A|B_i) is directly the probability of drawing i successes (blue balls) without replacement from a finite population of 10 total, with 5 “success” states (blue). This is the hypergeometric distribution formula ( (5 choose i)/(10 choose i) ).
Could we simulate this scenario in Python?
Yes. One could run a large number of trials to empirically estimate P(A) and P(B_r | A). Here is an illustrative code snippet:
import random
import math
def simulate(num_simulations=10_000_00):
count_all_blue = 0
count_r_and_all_blue = [0]*7 # indices from 0..6, we'll ignore 0
for _ in range(num_simulations):
# Roll a fair die
r = random.randint(1,6)
# Draw r balls from a jar of 5 blue + 5 red
jar = ['B']*5 + ['R']*5
drawn = random.sample(jar, r)
# Check if all are blue
if all(ball == 'B' for ball in drawn):
count_all_blue += 1
count_r_and_all_blue[r] += 1
# Probability of all blue
p_all_blue = count_all_blue / num_simulations
# Probability of B_r given A
p_given_all_blue = [0]*7
for r in range(1,7):
if count_all_blue != 0:
p_given_all_blue[r] = count_r_and_all_blue[r] / count_all_blue
return p_all_blue, p_given_all_blue
pA, pBr_givenA = simulate()
print("Estimated P(A):", pA)
for r in range(1,7):
print(f"Estimated P(B_{r} | A):", pBr_givenA[r])
Why is P(B_6 | A) = 0?
Since we cannot draw 6 blue balls from only 5 available, it is impossible for event A (all blue) to happen if the die roll is 6. Hence the conditional probability P(B_6 | A) must be 0.
What if the jar had more than 5 blue balls?
The formula would be modified accordingly. For instance, if there were m blue and n red balls in total, and you roll i, P(A|B_i) would become (m choose i)/(m+n choose i). The rest of the logic—summing over i using the fair die’s probability—remains the same.
What if the die were biased?
Then P(B_i) would no longer be 1/6. Suppose the probability of rolling i is p_i (with p_1+p_2+...+p_6=1). We would replace 1/6 by p_i in the relevant formulas, but the hypergeometric portion (5 choose i)/(10 choose i) would be unchanged.
These considerations highlight the general approach: break the problem via total probability across the possible die outcomes, compute the hypergeometric probability for each possible draw size, then sum/normalize accordingly.
Below are additional follow-up questions
Could we solve part (a) using a complementary event approach?
To use a complementary approach, we would consider the probability that at least one of the drawn balls is red, and then do 1 minus that probability. However, because each outcome depends on the die roll i, we would still need to sum or account for each possible i. In other words, computing 1 – P(“at least one red”) = 1 – Σ P(“at least one red” ∩ B_i). Even though complementary counting can be useful for some problems, in this scenario we still must handle different numbers of draws (i=1 to 6) distinctly. Therefore, the complementary approach is not necessarily simpler here—it requires summation across all die outcomes, just as in the direct approach. That said, in principle it works, but you would need:
1 – Σ over i=1..6 [P(“draw at least one red” | B_i)*P(B_i)].
And “draw at least one red” | B_i can be found by 1 – (5 choose i)/(10 choose i) for i=1..5, and is trivially 1 for i=6 because it’s impossible to draw 6 blue. You will ultimately arrive at the same 5/36 result for P(A).
A subtle pitfall is that if you attempt to combine events incorrectly (e.g., “at least one red” across different i’s as if they were identical events), you could double-count or miscount. Hence, you must carefully handle each die outcome separately.
Does the sequence in which we draw the balls matter to the final probability?
No, the probability that we end up with a specific combination of drawn balls (e.g., all blue) does not depend on the order of drawing under a uniform random draw without replacement. Whether we look at the sequence or simply the final selection of i balls, the probability of obtaining a particular subset is the same. A pitfall arises if someone mistakenly tries to count permutations (ordered draws) instead of combinations (unordered draws), which can lead to confusion or incorrect probabilities if not handled consistently. The fundamental hypergeometric formula accounts for combination-based counting, so the final result remains the same regardless of order.
What if we replace the drawn balls back into the jar after each draw (i.e., drawing with replacement)?
Drawing with replacement changes the underlying probability structure. If after drawing one ball you put it back (and mix), each draw would be an independent event. The probability P(A|B_i) in that case would be (number of blue/total)^i = (5/10)^i = (1/2)^i. Then we would still multiply by the probability of rolling i (1/6 in a fair die scenario) and sum over i=1..6. That would make part (a) into:
Sum_{i=1..6} [ (1/2)^i * (1/6) ].
This is a geometric-like series. For part (b), we would update P(B_r | A) accordingly using Bayes’ rule. The subtle pitfall is failing to recognize that the original problem states “without replacement,” and if someone inadvertently applies a “with replacement” formula, the probabilities will differ significantly.
How would the result change if we allowed the possibility of rolling a 0 on a (hypothetical) 7-sided die?
If, hypothetically, the die had possible outcomes 0 through 6 instead of 1 through 6 (and each face was equally likely), then the event B_0 (rolling zero) would mean no balls are drawn. In that scenario, drawing zero balls trivially yields “all drawn balls are blue” (since you drew none, none is a red ball). Consequently, P(A|B_0) = 1. You would then incorporate that scenario into the law of total probability:
P(A) = P(B_0)*1 + Σ_{i=1..6} P(B_i)*P(A|B_i).
A pitfall is incorrectly ignoring the case of drawing zero balls. In real-world usage, it’s unusual for a standard die to include zero, but hypothetically, if that happened (or if in some use case “no draw” was a possibility), we must handle it carefully in the summation.
If the die were loaded in such a way that rolling 5 or 6 is extremely likely, how would that affect the final probabilities?
The logic would stay the same, but P(B_i) would change. For instance, if the loaded die had P(B_5) and P(B_6) relatively high, then you would have a situation where the chance to draw 5 or 6 balls becomes more likely. In the standard scenario with only 5 blue balls, rolling a 6 means P(A|B_6) = 0. Because of the higher probability of rolling a 6 in a loaded scenario, that zero-probability portion would weigh more in the total. That would push P(A) down, since more weight is given to the draw-size scenario that makes it impossible to get all blue. The main pitfall is forgetting to re-normalize the new probabilities or incorrectly summing them to 1. Always ensure that the sum of your P(B_i) across i=1..6 is 1 when dealing with a biased die.
How would you approach the expected value of the total number of blue balls drawn across many trials?
To find the expected number of blue balls drawn, let X be the random variable denoting the number of blue balls in a single experiment. You would compute:
E(X) = Σ_{i=1..6} E(X | B_i)*P(B_i).
Now, E(X | B_i) is i*(5/10) = i*(1/2), because on average, out of i draws from a jar of 5 blue and 5 red, you would expect half to be blue. However, since drawing is without replacement, a more precise approach is to use the hypergeometric distribution’s expected value for i draws: i*(5/10) anyway. So the final result matches the simpler logic that, on average, half of the drawn balls will be blue. A subtle pitfall could be ignoring the fact that the number of draws i is itself random. The overall expected value requires weighting each E(X | B_i) by P(B_i), which is 1/6 for a fair die. This yields:
E(X) = (1/6) * [1*(1/2) + 2*(1/2) + ... + 6*(1/2)] = (1/2)(1/6) (1+2+3+4+5+6) = (1/2)(1/6) 21 = 21/12 = 7/4 = 1.75.
Could the outcome change if we repeated the entire experiment multiple times, each time removing the drawn balls permanently from the jar across trials?
Yes, if after each complete experiment (roll once, draw i balls, discard them entirely from the system) the jar did not get replenished, then the composition of the jar changes from one experiment to the next. Eventually, there might be fewer than 5 blue or fewer than 5 red balls (or even no balls at all if repeated enough times). This changes the probability distribution over time for subsequent experiments. In that scenario, the problem no longer has a fixed distribution of 5 blue and 5 red for every new trial. One would have to track how many blue and red balls remain after each experiment. This can become a more complicated Markov chain problem if multiple experiments are performed in sequence. A pitfall is to assume the distribution remains fixed when in reality it changes after each trial.
Would the probabilities be different if we used a 10-sided die and still had only 5 blue and 5 red balls?
Yes. If we used a 10-sided die labeled 1 through 10 (assuming equal probability 1/10 each), then for i=6 through 10 you cannot draw all blue because there are only 5 available. Consequently, P(A|B_i) = 0 for i=6..10. Only i=1..5 can yield all blue. Then the law of total probability becomes:
P(A) = Σ_{i=1..5} [ (5 choose i)/(10 choose i ) * (1/10 ) ].
Intuitively, you have more ways to roll a number of balls greater than the blue count, so you reduce the overall probability of drawing all blue. A subtle pitfall is that it’s easy to forget to recalculate the die probabilities or to incorrectly handle the new maximum i. You must keep track that P(A|B_i) is zero for any i > 5.