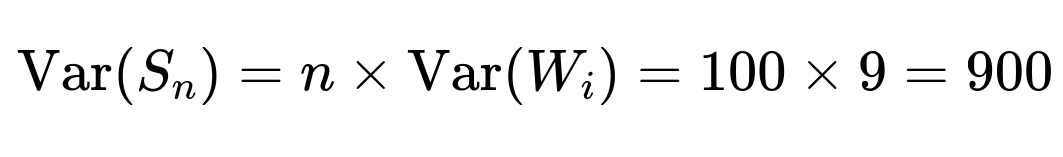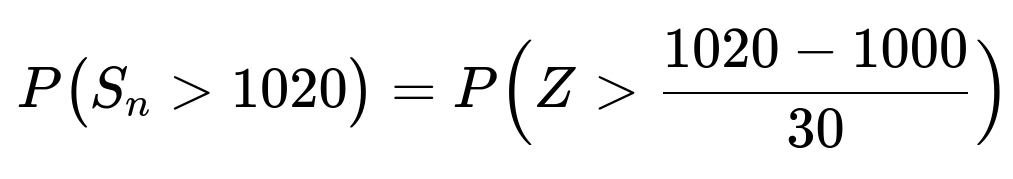ML Interview Q Series: Estimating Total Airfreight Weight Probability Using the Central Limit Theorem.

Browse all the Probability Interview Questions here.

An airfreight company has various classes of freight. In one of these classes, the average weight of packages is 10 kg and the variance of the weight distribution is 9 kg^2. Assuming that the package weights are independent (i.e., no single company is sending a large number of identical packages), estimate the probability that 100 packages will have a total weight more than 1020 kg.

Short Compact solution

Using the Central Limit Theorem, the total weight of 100 packages is approximately normally distributed with mean 1000 and variance 30^2. Therefore,

P(total weight > 1020) = P(Z > (1020 − 1000) / 30) = P(Z > 0.67) = 0.251

Comprehensive Explanation

Why the Central Limit Theorem applies

The Central Limit Theorem (CLT) states that if you have a set of independent and identically distributed random variables with finite mean and variance, their sum (or average) tends toward a normal distribution as the sample size grows large. Here, each package’s weight can be considered an independent random variable with a well-defined mean (10 kg) and variance (9 kg^2). With n=100 packages, it is typically large enough to invoke the CLT as a good approximation.

Modeling the total weight

Let W_i (in plain text) be the weight of the i-th package. We have:

• Mean of each package: 10

• Variance of each package: 9

We define the total weight S_n in plain text as:

Below are the mean and variance of S_n:

Hence the standard deviation of S_n is sqrt(900) = 30.

Thus, by the CLT, S_n is approximately N(1000, 30^2).

Computing the probability

We want P(S_n > 1020). Standardizing, we let Z be a standard normal random variable (mean 0, variance 1). Then:

The z-value is (1020−1000)/30 = 20/30 = 0.67. Looking up the standard normal table (or using statistical software) for P(Z > 0.67) gives approximately 0.251. Therefore, there is about a 25.1% chance that the total weight of the 100 packages exceeds 1020 kg.

Potential Follow-up Questions

What if the distribution of individual package weights is not normal at all?

Because of the CLT, we do not need the package weights themselves to be normally distributed. We only require that each W_i has the same distribution (i.i.d.) with finite mean and variance. For large n, the sum of W_i converges in distribution to a normal. If n were much smaller than 100, or if the variance were infinite, or if there were extremely heavy-tailed distributions, we might need to be cautious about applying the CLT.

How sensitive is this probability to small changes in mean or variance?

If the true mean were slightly different, say 10.2 or 9.8, or if the variance were different, the total distribution would shift or stretch accordingly. Because the standard deviation for the sum grows with sqrt(n), small changes in the package-level variance can be amplified. However, for practical shipping scenarios, these inputs (mean 10 kg and variance 9 kg^2) are usually estimated from sufficient historical data, ensuring decent accuracy.

Could we have used other probability bounds (like Chebyshev’s inequality) instead?

Chebyshev’s inequality provides a more general bound but is typically less tight for practical numerical estimates. It would tell us that the probability of deviating more than k standard deviations from the mean is at most 1/k^2. However, for a problem that involves a fairly large number of i.i.d. variables and finite variance, the CLT-based normal approximation is usually far more accurate.

How would we implement this probability calculation in Python?

One simple approach is to use a normal distribution function from a library such as scipy.stats. For example:

import math
import mpmath  # or you can use scipy.stats.norm

mean = 1000.0
std_dev = 30.0
threshold = 1020.0

z_value = (threshold - mean) / std_dev
# Using mpmath's erf or any standard normal distribution approach:
prob_exceed = 1.0 - 0.5*(1.0 + mpmath.erf(z_value / math.sqrt(2)))
print(prob_exceed)

This code computes P(Z > z_value), which is precisely the probability that the sum exceeds 1020.

What happens in a real-world scenario if packages are not truly independent?

If package weights are correlated (for instance, if some customers regularly ship near-identical items), the effective variance of the sum would change. Positive correlations tend to increase variance, leading to a higher chance of large deviations. Negative correlations do the opposite. In practical airline freight, it is often safe to assume approximate independence unless there is evidence that many packages come from the same shipper or are systematically linked.

Could outliers (very heavy packages) invalidate the CLT approximation?

If the distribution has significant outliers or a heavy tail, the variance might be underestimated or might not be finite in extreme cases. The CLT still applies under a wide range of conditions (specifically, the Lindeberg condition), but if outliers are common, one might need other robust or non-parametric methods. In many real shipping contexts, extremely heavy outliers are less likely due to class restrictions, size limits, or cost considerations.

How would we handle a scenario where package counts are unknown or vary?

If the exact number of packages is random or if we only have a distribution for n itself, we could treat n as another random variable. We would then need the law of total expectation and total variance, or a compound model. In most standard shipping scenarios, n is fixed by the order of shipments, making the simpler approach sufficient.

All these considerations highlight that while the CLT method is quick and powerful, one must assess whether conditions like independence and identical distribution hold and whether there are any extreme values or correlations that could invalidate the assumptions.