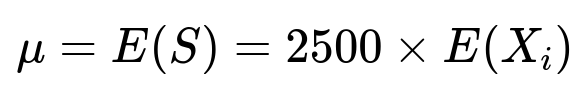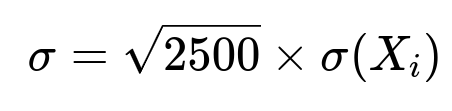ML Interview Q Series: Estimating Casino Loss Probability for Roulette Promotion using Normal Approximation.

Browse all the Probability Interview Questions here.

A new casino has just been opened. The casino owner makes the following promotional offer to induce gamblers to play at his casino. People who bet $10 on red get half their money back if they lose the bet, while they get the usual payout of $20 if they win the bet. This offer applies only to the first 2,500 bets. In the casino, European roulette is played so that a bet on red is lost with probability 19/37 and is won with probability 18/37. Use the normal distribution to approximate the probability that the casino owner will lose more than $6,500 on the promotional offer.

Short Compact solution

Define X_{i} as the amount (in dollars) the casino owner loses on the i_{th} bet. Then X_{1}, X_{2}, …, X_{2500} are independent, with P(X_{i} = 10) = 18/37 and P(X_{i} = -5) = 19/37. The expected loss on a single bet is 85/37 ≈ 2.29730, and the standard deviation is approximately 7.49726. By the Central Limit Theorem, the total loss over 2,500 bets is approximately normal with mean 2.29730 × 2,500 ≈ 5,743.25 and standard deviation 7.49726 × sqrt(2,500) ≈ 374.863. The probability that the total loss exceeds 6,500 is about 1 − Φ((6,500 − 5,743.25) / 374.863) ≈ 0.0217.

Comprehensive Explanation

Background on the random variable for a single bet

When someone bets $10 on red under this promotion, two outcomes are possible. With probability 18/37, the player wins, and the casino must pay out $20 (that is a $10 profit for the bettor, so the casino effectively loses $10). With probability 19/37, the bettor loses, but only loses half of the $10 stake, so the bettor gets $5 back and the casino loses −$5 (meaning the casino actually gains $5 relative to paying out $10, so from the casino’s perspective this is a negative loss of 5 dollars, i.e. X_{i} = −5). However, to keep things consistent with the problem statement, we label the casino’s loss in the losing outcome as −5. Thus:

P(X_{i} = 10) = 18/37 P(X_{i} = −5) = 19/37

Expected value of X_{i}

The expected loss on a single bet can be computed as:

This evaluates to 180/37 − 95/37 = 85/37 ≈ 2.29730. This indicates that on average, the casino loses approximately $2.30 per bet under this promotion.

Variance and standard deviation of X_{i}

To find the variance, we first compute E(X_{i}^2). Because X_{i} only takes on two values:

E(X_{i}^2) = (10^2) × (18/37) + ((−5)^2) × (19/37) = 100 × 18/37 + 25 × 19/37.

Then the variance is Var(X_{i}) = E(X_{i}^2) − (E(X_{i}))^2. Plugging in the numbers yields approximately 7.49726^2 for Var(X_{i}), so σ(X_{i}) ≈ 7.49726.

Sum of 2,500 such bets

Let S = X_{1} + X_{2} + … + X_{2500}. By the linearity of expectation:

and since the X_{i} are i.i.d.,

In numerical terms:

Approximation via the Central Limit Theorem

The Central Limit Theorem tells us that for large n, S is approximately normally distributed:

Hence, we want the probability that the total loss S exceeds 6,500. Standardizing, we look at:

Substituting μ ≈ 5743.25 and σ ≈ 374.863:

The z-value is (6,500 − 5,743.25) / 374.863 ≈ 2.019. We then compute 1 − Φ(2.019), which is about 0.0217, or 2.17%.

Tricky Follow-Up Questions

How would the approximation change for a different number of bets?

If the number of bets is smaller, the normal approximation may be less accurate. With fewer than, say, 30 bets, the Central Limit Theorem is less reliable. In that case, an exact calculation of the distribution or a different approach (such as simulation) would be more appropriate.

What if the bets are not independent?

The Central Limit Theorem used here relies on the assumption of independent bets. If, for instance, there is some dependency or correlation between the outcomes of different bets, the variance of the total sum would no longer be simply 2,500 times Var(X_{i}). One would have to incorporate the correlation terms into the variance calculation, affecting the final probability estimate.

How can we perform a simulation to check this approximation?

One can write a quick simulation in Python that draws 2,500 samples from the discrete distribution P(X_{i} = 10) = 18/37, P(X_{i} = −5) = 19/37, sums them, and repeats many times (e.g., 100,000 trials). The fraction of trials where the total exceeds $6,500 is the estimated probability. For instance:

import numpy as np

n_sims = 100_000
n_bets = 2500
p_win = 18/37
sim_results = []

for _ in range(n_sims):
    # Generate 2500 outcomes
    outcomes = np.random.choice([10, -5], size=n_bets, p=[p_win, 1 - p_win])
    sim_results.append(outcomes.sum())

sim_results = np.array(sim_results)
prob_exceed_6500 = np.mean(sim_results > 6500)
print(prob_exceed_6500)

This simulation would yield a probability close to the value computed by the normal approximation, confirming or contrasting the theoretical result.

What if the question asked for a more precise probability, not just an approximation?

To get a more precise probability, you would ideally sum up the exact binomial-like distribution that arises from having a certain number of “wins” (X_{i} = 10) out of 2,500. Specifically, the total loss can be written as 10W + (−5)(2,500 − W) where W is the number of wins, and W follows a Binomial(2,500, 18/37). You could compute P(S > 6,500) directly by summing P(W = w) for the appropriate range of w. However, this exact method involves large binomial coefficients and may be computationally expensive, though it is numerically feasible with efficient binomial probability functions for 2,500 trials.

Below are additional follow-up questions

How would you use a continuity correction when applying the normal approximation for a discrete underlying distribution?

When the number of bets is large, the discrete nature of the sum of bets can be approximated well by a continuous distribution. However, one might wonder if adding a continuity correction term would yield better accuracy. In a binomial setting, a continuity correction is typically used when approximating P(X ≥ x) by converting it to P(X > x − 0.5) in the normal domain. In our context, although each individual X_i is not purely binomial (because X_i takes values 10 or −5), the total sum can still be expressed in terms of the number of wins (W) times 10 plus the number of losses times −5. Formally:

S = 10W + (−5)(2500 − W).

Since W itself is binomial with n = 2500 and p = 18/37, one could apply a continuity correction to the distribution of W. For instance, to compute P(S > 6500), we translate that into an inequality in terms of W:

6500 < 10W + (−5)(2500 − W) = 10W − 5(2500) + 5W = 15W − 12500.

Hence, 15W > 6500 + 12500, or 15W > 19000, so W > 19000/15 = 1266.66….

For a continuity correction, you might consider P(W ≥ 1267) as P(W > 1266.5) in the binomial setting, then approximate W by a normal distribution with mean n·p and variance n·p·(1−p). This, however, is an additional layer of approximation on top of how the payoffs translate to final sums. Because the normal approximation for n = 2500 is already quite strong, the continuity correction’s impact is often modest. In large-sample settings, the effect may not significantly change the final answer, but it could be theoretically more accurate in borderline cases.

Pitfalls and edge cases:

• Continuity corrections matter more for smaller sample sizes where the discrete jump between integer values is relatively large compared to the distribution’s spread.

• In very large n situations, the difference due to a continuity correction is almost negligible and can be overshadowed by real-world variability or correlation effects.

What if the payout structure changes during the promotion, creating different random variables over time?

In a real casino setting, the owner might decide to adjust the promotional offer after observing preliminary results. For example, they might reduce or increase the number of losing bets that pay half if the casino is losing too much. Such a scenario creates piecewise or time-varying random variables:

• For the first k bets, you have the old structure (win yields −10 from the casino’s perspective, losing yields −5).

• For the remaining (2500−k) bets, you might have a new structure or revert to standard roulette payouts.

In that case, the random variable for each bet no longer follows the same distribution over all 2500 trials. One would need to consider the sum of multiple random variables that are i.i.d. only in segments. For instance, define:

X_1, X_2, …, X_k ~ distribution D_1 X_{k+1}, …, X_{2500} ~ distribution D_2.

You could then compute the mean and variance separately for each segment and sum them:

mean of S = k × E(X_i from D_1) + (2500−k) × E(X_i from D_2),

variance of S = k × Var(X_i from D_1) + (2500−k) × Var(X_i from D_2),

assuming independence across bets. Then you could still apply the Central Limit Theorem if k is not too small and the second segment (2500−k) is sizable. However, if these changes happen rapidly or frequently, you may need a more general approach (possibly simulations) to handle frequent distribution shifts.

Pitfalls and edge cases:

• If the new structure drastically changes the payoff, the overall variance might be dominated by one portion of the bets.

• If the transition from the old structure to the new structure depends on prior outcomes, there is a built-in dependency that complicates standard CLT assumptions.

How would limiting the maximum number of bets per person affect the total loss distribution?

Sometimes, casinos impose limits on how many times a single gambler can take advantage of a promotional deal. For example, each person can only place a limited number of promotional bets. If each individual gambler is subject to a cap, and different gamblers participate, you can typically still model each bet as an i.i.d. random variable (assuming different gamblers are unrelated). The distribution for S remains approximately the same if we assume the probability of winning or losing is unaffected by player skill (for roulette, skill does not matter).

However, if a single gambler makes many promotional bets in a row, there could be “gambler’s ruin” type behaviors or strategic betting changes—though for a fair or near-fair game like roulette, these strategies have limited real effect on the distribution. The main effect might be social or psychological: gamblers might alter bet sizes or frequency in real life, but from a purely mathematical perspective of expected payout in roulette, limiting the number of bets per person does not alter the fundamental distribution if each bet is still identical in its probability structure.

Pitfalls and edge cases:

• If the limit is very restrictive (e.g., each person is allowed only one bet), we might have a smaller total number of bets or a skew in the distribution of bet outcomes.

• If the promotional bets are quickly exhausted by highly frequent players, the correlation of bets might increase because the same few players might be playing repeatedly, potentially introducing small dependencies.

How does the house edge in European roulette compare to other games, and does it change the normal approximation approach?

European roulette, with a single zero, has a house edge of 1/37 (roughly 2.70%). However, with the promotional offer, the effective “house edge” for these bets is no longer standard. We’ve computed an expected casino loss of about $2.30 per $10 bet, indicating this particular promotion is unfavorable to the casino. If you switched to American roulette (which has two zeroes, giving a higher house edge in normal circumstances), the probabilities would be different (for instance, probability of losing might be 20/38 for red, probability of winning might be 18/38, ignoring green for this example).

As for the normal approximation, the change in the underlying probabilities and payouts merely changes the mean and variance of each individual bet. The mechanism of the Central Limit Theorem remains valid for i.i.d. bets (though the expected value might be different). You would continue to approximate the sum using a normal distribution with updated parameters:

• Updated E(X_i) based on the new payouts/probabilities.

• Updated σ(X_i) as the square root of Var(X_i).

• Then use N( n × E(X_i), n × Var(X_i) ) for large n.

Pitfalls and edge cases:

• Even though the basic approach remains, if the difference in probabilities is marginal, you must pay special attention to the variance. A small shift in probabilities can still cause large changes in the standard deviation if the payouts differ greatly.

Could a large deviation principle or Chernoff bound be more appropriate than the CLT in certain risk assessments?

The Central Limit Theorem is most convenient when we only care about events that are not extremely far from the mean. If you want to assess very rare events (e.g., the probability that the casino loses a dramatically large amount far beyond 6500), large deviation principles might be more accurate. Chernoff bounds or Hoeffding’s inequality give exponential bounds on the tail probabilities of sums of i.i.d. random variables. They are often used to get conservative estimates of tail risk without requiring exact distributional forms.

However, in practice, for a real casino scenario with n = 2500 and a moderately sized deviation like 6500 − 5743.25 ≈ 756.75, the CLT typically provides a decent approximation. If we were interested in extremely large losses (like losing more than $10,000 or $15,000), a large deviation analysis might be more reliable.

Pitfalls and edge cases:

• Chernoff or Hoeffding bounds typically give upper (often pessimistic) limits on the tail probability, which might be too conservative for practical risk management—leading, for instance, to unnecessary hedging.

• In a scenario with extremely high payoffs or bonus multipliers, the tail distribution might be heavily skewed, and a standard CLT approach might underestimate tail probabilities.

What if the bets are placed sequentially and the house adjusts the promotion dynamically based on intermediate results?

In real life, if the casino sees it is losing too much money, they might change or cancel the promotion midstream. This scenario introduces a dependency between earlier and later bets. Instead of having 2500 i.i.d. bets, the distribution for the “later” bets depends on results from the “earlier” bets.

For instance, if the house sets a threshold that if they lose more than $2000 in the first 100 bets, they stop the promotion, then the random variable S is truncated in some manner. The overall distribution is then a mixture of:

• The sum of 100 bets if the threshold is reached early.

• Potentially up to 2500 bets if the threshold is never reached.

This breaks the standard i.i.d. assumption and complicates the direct application of the CLT. A typical approach is:

1. Model the problem as a stochastic process with absorbing states (once the threshold is hit, the promotion ends).

2. Use Markov chain methods or direct simulation to find the distribution of total losses.

Pitfalls and edge cases:

• The distribution might become multimodal because there is one mode centered on the situation where the casino halts early, and another mode near the full 2500 bet scenario.

• Analytical approximations can become unwieldy, so simulation might be more straightforward.

How would you create a confidence interval for the expected casino loss rather than just a point estimate?

While the question focuses on the probability of exceeding $6500, you may also need a confidence interval for the expected total loss to inform financial planning. Since each bet has expected loss E(X_i) = 85/37, a natural point estimate of the total expected loss is 2500 * (85/37). To create a confidence interval:

1. Use the sample mean from actual data (e.g., from observing a subset of bets) as an estimate of E(X_i).

2. Estimate the variance from that same subset.

3. Rely on normal approximation for the sample mean of X_i if the number of bets observed is large.

For instance, if M is the average loss per bet in a random sample of m bets, the approximate (1−α)100% confidence interval for the true average loss per bet could be:

M ± z_{α/2} * (sample standard deviation / sqrt(m)).

Then multiply the interval endpoints by 2500 to get a confidence interval for the total promotional loss. Alternatively, a Bayesian approach could incorporate a prior distribution on E(X_i) or on the difference from the standard house edge.

Pitfalls and edge cases:

• If the observed data is not representative (e.g., due to lucky streaks or unusual gambling behavior in the early sample), the interval may be misleading.

• Correlations among bets or changes in the promotion structure can invalidate the simple i.i.d. assumptions behind standard confidence interval methods.

How do minor variations in bet sizes (for instance, different players wagering a different amount than $10) affect the probability calculation?

In the real world, a casino might allow variable bet sizes, although the promotion specifically mentions $10 on red, then half back if you lose. If the promotion permitted “bet at least $10” or allowed multiple denominations (like $20, $50, etc.), you can no longer treat each bet as having the exact same distribution. You would then have:

X_1, X_2, …, X_{2500} ~ i.i.d. only if the bet sizes are identical.

But if bet size can vary, one might approximate each bet by some average bet size or build a mixture model of distributions:

• With probability p1, the bet is $10, leading to the random variable distribution we have.

• With probability p2, the bet is $20, leading to a different random variable for the casino’s loss.

• And so on for any allowed denominations.

Then S is the sum of a mixture of random variables. One approach is to:

1. Estimate the proportion of each bet size.

2. Compute the mean and variance for each bet size.

3. Combine them to find the overall mean and variance for a “typical” bet.

4. Proceed with CLT if the total number of bets is large.

Pitfalls and edge cases:

• If high rollers significantly skew the distribution because they place a small number of extremely large bets, the normal approximation might underestimate tail risk.

• If the distribution of bet sizes changes over time (e.g., big bettors show up late in the promotion), i.i.d. assumptions do not hold consistently throughout.

How would you account for gambler’s preferences or strategies that might change the probability of red vs. other bets?

The question focuses on bets on red. In reality, players might switch between red, black, odd, even, or place inside bets on specific numbers. If the promotion is strictly “bet on red for $10 to get half back if you lose,” it forces a single type of bet. However, gamblers might choose not to bet if they dislike the promotion or might exploit other games. This scenario introduces selection bias in the actual number of promotional bets placed:

• Some gamblers might never take advantage of the promotion if they incorrectly believe it’s unfavorable.

• Others might overuse it if they realize it’s a good deal.

In a simplistic model ignoring gambler psychology, we still treat all 2500 bets as placed. In real life, you need to analyze how many players will actually wager, which affects the total number of bets and the distribution of outcomes. The normal approximation is only valid if you do reach 2500 bets with the same distribution each time.

Pitfalls and edge cases:

• If fewer than 2500 bets are placed, the total distribution changes.

• The actual expected loss to the casino might be lower if not all promotional bets are utilized, or it might be higher if primarily advantage-seeking players exploit the promotion heavily.

What if there are “repeat wins” or “hot streak” perceptions influencing bet outcomes?

In strict probability theory, each spin of the roulette wheel is an independent trial. However, gamblers might believe in streaks or “hot” numbers, adjusting their bets accordingly. If these superstitions have no effect on the actual physical randomness, the distribution remains i.i.d. from the roulette outcome perspective. From the casino’s viewpoint, the probability of red remains 18/37.

But if mechanical or physical biases exist (e.g., a faulty roulette wheel that actually hits red with a probability higher than 18/37), the expected loss changes:

• Let the true probability of red be p instead of 18/37.

• Then the expected value of each bet is 10×p + (−5)×(1−p).

This could cause a systematic deviation from the theoretical value. One must estimate p from real spins data or engineering tests on the wheel. If p > 18/37, the casino is in worse shape than it believes.

Pitfalls and edge cases:

• Even a tiny deviation in p can compound over 2500 bets to create a notable shift in total losses.

• If mechanical bias is discovered partway, the promotion or the wheel might be changed, leading to a shift in the distribution mid-promotion and invalidating naive i.i.d. assumptions.

How might you extend this analysis if players can double their bets or split them across multiple different outcomes?

In many casino games, players have the option to double down or split (though that’s more common in blackjack than roulette). In roulette, you can bet multiple areas simultaneously. If the promotion allowed partial bets on red plus inside bets, the distribution of outcomes becomes more complex. You’d need to define random variables reflecting a combination of possible outcomes:

• Part of the $10 is on red (with the half-loss promotion).

• The rest might be on a single number or a corner bet, each with different payouts.

In a typical roulette payout table, single numbers pay 35:1, splits pay 17:1, and so forth. The presence of multiple bet types changes:

• The probability distribution of each spin’s payoff.

• The dependence between wagers on the same spin (though from the house perspective, the total outflow is a single random variable for that spin).

If the promotional half-loss only applies to the portion of the bet on red, then you would effectively have a mixture distribution for each spin. The normal approximation can still be applied for large numbers of spins, but you must compute the new distribution’s mean and variance carefully by summing up the expected payoffs from each fractional component of the bet.

Pitfalls and edge cases:

• Overlooking correlation between bets (e.g., if part of the bet is on red and part is on black, these outcomes are not independent).

• Handling the possibility that some players place the entire $10 on a single number, drastically increasing variance.