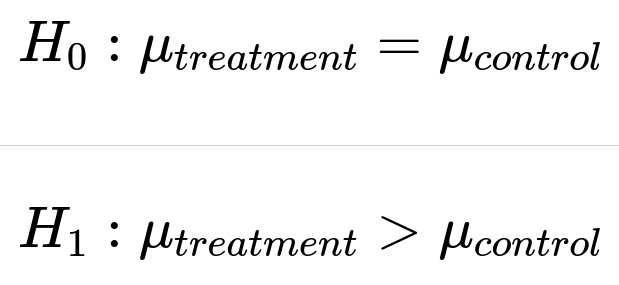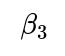ML Interview Q Series: Evaluating Driver App UI Impact on Ride Volume via A/B Testing

Browse all the Probability Interview Questions here.

Your team wants to see if a new driver app with extra UI features will increase the number of rides. How would you test that these extra features make it better than the original version?

Planning and executing a well-structured online experiment or A/B test is generally the most direct approach to assess whether the new UI features actually result in more rides. Below is a detailed discussion of the entire process, potential pitfalls, and the depth of reasoning behind each step.

Designing The Experiment

You want to set up a controlled experiment that compares two versions of the driver app:

• Control version is the existing driver app. • Treatment version is the new driver app that has extra UI features.

The fundamental idea is to split your driver population randomly so that you assign some drivers to the control group and the rest to the treatment group. The random assignment ensures that, on average, both groups are comparable in all aspects apart from the new UI features. Then you measure how many rides each group logs over a specified time period.

Key Points In Designing The Experiment

Random Assignment Randomization is the foundation of a valid experiment. You might randomly assign a fraction (for example, 50%) of your driver population to experience the new UI. The remainder sees the original UI. Because assignment is random, the only systematic difference between the two groups should be the presence or absence of the new UI.

Avoiding Leakage or Contamination Some drivers could inadvertently see multiple versions if they have multiple devices or if your system inadvertently toggles them between versions. Ensuring consistent exposure (e.g., once assigned to the new UI, you always see it) is critical for clean data.

Choosing Proper Metrics The question specifically focuses on the number of rides. However, you might also want to track other operational metrics like average ride duration, drop-off rates during ride matching, or driver retention. The primary metric (key performance indicator) is total number of rides per driver in the treatment group versus control group, averaged over the experimental period.

Length and Timing of the Test An experiment generally runs until you have collected enough data to make a statistically significant decision. This depends on your typical traffic (i.e., how many rides are logged daily), the expected effect size (how big an improvement you anticipate), and the desired statistical power.

Hypothesis and Statistical Testing

Formulate The Hypothesis Set up a null hypothesis and an alternative hypothesis:

Here,

is the average number of rides per driver for the treatment group, and

is that of the control group. The null hypothesis states there is no difference, while the alternative states the new UI features yield a higher average number of rides.

Statistical Significance And Confidence Interval You might use a standard two-sample t-test or a non-parametric test to compare the means. Or you might use a proportion test if the outcome can be modeled in a certain way (e.g., rides taken or not). If you want to approach the problem from a more distribution-agnostic perspective, you could use a bootstrap approach.

Sample Size And Power Considerations You need enough users in each group to reliably detect a difference, if one truly exists. If the change in the new UI is expected to produce only a small (but valuable) percentage increase in rides, you must plan for a correspondingly larger sample size to detect that small difference with statistical significance. Tools or formulas exist to compute the minimum sample size. If

is the significance level (e.g., 0.05) and

β=1−power

(e.g., 0.8 or 0.9), typical sample size formulas revolve around the effect size and standard deviations.

Practical Implementation Considerations

Rollout Strategy Depending on organizational culture, you can do a 1% pilot test first to spot potential issues and limit risk. Once stable, you scale the test to a larger percentage of your driver population.

Data Collection Pipeline You need robust instrumentation in the app to track how many rides are completed by each driver, whether that driver is in control or treatment, and how often they actually engage with the new UI features.

Segmentation It might be useful to segment by geography, driver tenure, platform type (Android vs. iOS), or usage patterns. This helps you see if the new UI disproportionately benefits certain groups.

Analyzing Results

Comparing Means Or Proportions A typical approach is to compute the average number of rides in each group:

• ParseError: KaTeX parse error: Can't use function '$' in math mode at position 30: …ext{treatment} $̲$ = average rid…

Then measure the difference

. Use a hypothesis test to assess if

δ

is statistically significant.

Confidence Interval A confidence interval for

δ

can provide more interpretability. If the 95% confidence interval for

δ

is, for example, [1.5, 2.0], you have evidence that the new UI leads to between 1.5 and 2.0 additional rides on average per driver in the test period.

Assessing Practical Significance Even if a difference is statistically significant, it is important to see whether it is big enough in practical or financial terms. For instance, if you see a statistically significant improvement of 0.01 additional rides per driver, that may or may not be important depending on ride volume and margins.

Potential Pitfalls And Edge Cases

Adoption Lag Drivers might need time to adapt to the new interface. A short test might not capture the real long-term impact. Consider measuring how the effect evolves over days/weeks.

Seasonality Or External Factors If you run the experiment during a holiday season, or in particularly slow periods, that might skew the results. Randomization usually helps, but you should be aware of unusual external factors.

Interaction With Other Features If other new app features or promotions roll out concurrently, it becomes harder to isolate the effect of the new driver UI. Coordination across product teams is key to preserve the “all else being equal” principle.

Observational Biases If some part of your driver population is inadvertently excluded or included in a skewed manner, it can bias your estimate. For example, if older devices cannot support the new UI, then your randomization is effectively compromised. You need to ensure equal chance of assignment at the device or driver ID level.

Implementation Example (High-Level Python Pseudocode)

import numpy as np
from scipy import stats

# Suppose you have arrays of daily rides for each driver in the treatment and control groups
treatment_rides = np.array([/* daily rides per driver for treatment group */])
control_rides   = np.array([/* daily rides per driver for control group */])

# Perform a two-sample t-test
t_stat, p_value = stats.ttest_ind(treatment_rides, control_rides, equal_var=False)

print("T-statistic:", t_stat)
print("P-value:", p_value)

# You might also construct confidence intervals manually or using your stats library
# For demonstration, let's do a basic example for difference of means
mean_diff = treatment_rides.mean() - control_rides.mean()
std_treat = np.std(treatment_rides, ddof=1)
std_ctrl  = np.std(control_rides, ddof=1)
n_treat   = len(treatment_rides)
n_ctrl    = len(control_rides)

# Standard error for difference of two independent means
# Use Welch's approximation for standard error (assuming unequal variances)
se_diff = np.sqrt((std_treat**2 / n_treat) + (std_ctrl**2 / n_ctrl))

# 95% confidence interval
z = 1.96  # for 95%
ci_lower = mean_diff - z * se_diff
ci_upper = mean_diff + z * se_diff

print("Mean difference:", mean_diff)
print(f"95% CI: [{ci_lower}, {ci_upper}]")

This snippet is a simplistic demonstration of comparing two sets of data using a two-sample t-test and then constructing a confidence interval around the difference of means.

What If The Measured Metric Is Very Noisy?

If ride counts vary widely across drivers and the distribution is highly skewed, you can consider a log transformation of the metric or apply a non-parametric test (like the Mann-Whitney U test). Alternatively, a bootstrap approach can robustly estimate confidence intervals without strong distributional assumptions. The main idea remains that you compare the metric between control and treatment in a consistent and unbiased manner.

How Would You Handle Multiple Experimental Variations?

Sometimes, you might want to compare more than two variations of the driver UI (for example, different UI layouts or color schemes). One approach is to expand the design to an A/B/C test and ensure you have enough participants in each arm to detect differences. Another approach is to use multi-armed bandit techniques that adaptively allocate more users to the variation that appears to be performing best so far. However, if you do pure multi-armed bandits, you should be careful with how you compute final significance. Frequentist bandit approaches are trickier in maintaining a simple interpretation of p-values, while Bayesian bandit methods can incorporate prior distributions more smoothly.

How Would You Account For Covariates?

You might discover that some drivers have distinct usage patterns. For example, high-volume drivers (who drive 6-8 hours a day) might respond differently to the new UI than casual drivers. You can run a stratified analysis or incorporate regression-based methods where you include relevant covariates (like driver experience level or region) to isolate the effect of the UI. A typical approach might be:

Here, UI_treatment is a binary indicator variable (0 for control, 1 for treatment). The coefficient

measures the adjusted impact of the new UI on the number of rides, controlling for other factors in the model.

How Do You Decide If You Can Roll Out The Changes?

You look at both statistical significance (is the result real, not due to random chance?) and practical significance (does it move the needle enough to justify the engineering and rollout costs?). You also weigh any potential negative impacts discovered in your metrics (e.g., driver satisfaction issues, increased app load times, or complicated UX in corner cases).

If the experiment data demonstrates that the new UI significantly increases the average number of rides per driver and you see no detrimental effects on other important metrics, that supports rolling out the features more broadly. If the data shows no improvement, or even some degradation, you’d investigate possible reasons and possibly scrap or refine the new features.

---

Below are additional follow-up questions

What if the new UI has a learning curve for drivers and initial usage drops before eventually improving?

A new user interface can be intimidating or unfamiliar at first, causing drivers to be less efficient initially, resulting in fewer rides. Over time, as they grow accustomed to the new layout and features, their engagement and ride volume may rebound or surpass the baseline. This learning-curve effect can mask the true benefit of the new UI if the experiment is not run long enough or if early negative signals cause premature termination of the test.

One way to handle this is to run the experiment for a sufficient duration to capture the entire adoption curve. You can plot ride volume over time (for both the control group and the treatment group) to see how the metric evolves. If there is an initial dip, you may detect it by observing that the treatment group’s metrics start below control but later cross over and increase. Segmenting by drivers’ exposure time to the new UI (e.g., days since first exposure) can help quantify how quickly users adapt. It is common in UI-related experiments for the “time since assignment” factor to affect performance outcomes.

In real-world scenarios, you might mitigate the shock by providing tutorials or tooltips within the new UI. You might also consider rolling out the new UI gradually to smaller cohorts, observe how quickly they adapt, then extrapolate to the broader population. This ensures you do not risk widespread adoption of a UI that has an irreversible negative impact if the learning curve is too steep.

How do we avoid confusing A/B test results with normal seasonal variations or large external events?

External factors like holidays, severe weather, local festivals, or global events can significantly change ride patterns. Even well-randomized experiments can get confounded by these events if they occur after the experiment has launched but before completion. Although randomization helps distribute typical day-to-day variance across control and treatment, large or unusual disruptions can still cause interpretive challenges.

To mitigate this:

• Plan experiments around major known events. Avoid starting or stopping tests during major holidays. • Monitor both groups’ metrics closely for parallel changes. If both groups experience the same spike or dip, then the difference between them might still remain valid. • Extend the testing period to allow enough observations before and after any such events. • If you have historical data that shows typical seasonal patterns, compare your observed metrics to what is normally expected. For instance, if you know ride demand is generally 30% higher during holiday seasons, make sure to calibrate or run the test sufficiently before or after that spike. • If an unexpected major event occurs mid-test, you might need to pause or re-run the experiment depending on severity. For a short-term but severe disruption, you can potentially exclude that period from the analysis (with caution) if it’s clear that this period was extraordinary and equally impacted both groups.

How do you handle drivers who frequently switch between multiple devices or accounts?

Some drivers may have multiple smartphones or switch between personal and shared devices. This can lead to inconsistent exposure if your experiment assignment is not carefully enforced at the account or device level. If you randomize based on driver ID (account-based), but the user occasionally logs into a different account that might be in the opposite experimental group, you risk contamination.

To address this:

• Assign treatment at the unique driver ID level rather than device level, ensuring that, no matter which device the driver logs in from, they see the same UI version. • Implement checks to detect drivers who appear to maintain multiple active accounts. Such behavior might violate your platform’s terms of service or might signal an edge case that requires separate handling. • If a driver does somehow have multiple valid accounts for legitimate reasons (e.g., multiple fleet affiliations), randomization may have to ensure both accounts are placed in the same group if that driver is indeed a single individual.

You also want robust logging that can track which UI version was actually served to that driver at each usage event. If you detect a mismatch, you can remove or flag that usage data to avoid muddling your results.

What if the new UI changes driver acceptance rates for certain ride requests rather than strictly increasing overall volume?

Even if the total number of rides does not change drastically, the new UI might prompt drivers to accept certain types of rides they previously avoided (long-distance, surge areas, complex routes). Consequently, the distribution of ride types in the treatment group might be different from the control group. This does not necessarily reflect an absolute increase in total rides but could alter the nature of those rides.

You can investigate by segmenting rides based on:

• Ride duration • Profitability or surge factor • Time-of-day acceptance patterns

If you notice that the new UI causes a shift in which rides are accepted, it could still be beneficial (e.g., more profitable rides) even if total rides remain similar or only slightly increased. To measure overall impact, you might incorporate additional metrics like revenue per driver, ride acceptance ratio, or driver satisfaction scores.

Statistically, you could perform a difference-in-differences style comparison on subcategories of rides to see where the impact is largest. If your main goal remains “total rides,” you should still track how behavior changes across ride types, because it might highlight that the new UI is more or less effective in different ride contexts and that your success criteria need to account for this complexity.

How do you handle a situation where a sub-population of drivers responds negatively while others respond positively, netting out to a near-zero overall effect?

Sometimes, an overall average hides significant heterogeneity: the new UI might work very well for certain demographics (e.g., tech-savvy drivers) but is detrimental for another segment (e.g., drivers using older devices or less familiar with advanced features). This can cause the net impact to look negligible even though there are strong positive and negative sub-trends.

You can address this by:

• Breaking down your data by relevant covariates such as driver experience, the device’s operating system version, or region. • Comparing each subgroup’s difference in ride volume separately to identify which sub-populations thrive and which struggle. • Using an interaction term in a regression framework that captures the effect of the new UI for different subgroups. For instance, you could model:

Here, the interaction coefficient

shows how different the effect of the new UI is for drivers in that subgroup.

By identifying these sub-populations, you might either create specialized UI variants or provide targeted training resources to help those who respond negatively. It also informs whether the overall launch strategy should involve partial rollouts or customizing the UI for different segments.

If the new UI includes advanced features, how do you measure whether drivers in the treatment group actually used those features?

When your treatment variant offers new capabilities, some drivers may opt to continue using it in the same way as the old UI, effectively not accessing the additional tools. This partial adoption can dilute the measured treatment effect if you simply compare average rides in treatment vs. control, because many “treatment” drivers never truly engage with the new functionality.

To handle this, you can track feature usage within the new UI group. For instance, log every tap or navigation that specifically relates to the new features. Then, segment the treatment group into “engaged” (those who use the new UI features significantly) vs. “unengaged” (those who do not). Compare these subgroups to the control group. You might find that the new features are extremely beneficial for those who adopt them, while the aggregated average effect is muddied by drivers who never tried them.

This approach can also help you plan next steps: if the new features are valuable only to a small fraction of drivers, you might decide to refine the UI introduction or tutorials to encourage broader usage. Conversely, you might discover that minimal usage is due to the features not being intuitive or beneficial enough.

How do you adjust your analysis if the main success metric changes over time or if the app experiences general trending improvements unrelated to the UI?

Some ride platforms experience steady growth or cyclical fluctuation over time. Even if you have a randomized control group, both groups might see an upward or downward trend in ride volume due to marketing campaigns, expansions into new areas, or parallel platform enhancements.

A typical method to handle trending data is to use a “pre-post” design combined with control. If you have baseline data for each driver before the experiment starts, you can measure the change from baseline for each group, rather than just raw values in the treatment period. This can help isolate the incremental effect of the UI from broader platform-wide or time-based trends. Another approach is difference-in-differences:

• For each driver, measure the difference between their rides in the pre-experiment window and in the experiment window. • Compare those differences between treatment and control.

If the entire driver population is improving by some background rate, difference-in-differences helps remove that common lift. You can also run more sophisticated time-series analysis if the background trend is strong and you have historical data to model typical growth.

How do you handle concurrency with other ongoing experiments that might affect driver behavior?

In large-scale systems, multiple product teams may simultaneously run experiments. These concurrent tests could impact the same driver base—perhaps there’s an incentive campaign or surge-pricing algorithm experiment in parallel. This can lead to confounded measurements where you can’t isolate which experiment caused changes in ride volume.

To mitigate these issues:

• Coordinate with other teams to ensure that the same driver population is not subject to overlapping experiments that affect the same key metrics. • Use a mutually exclusive holdout approach, where each experiment draws from distinct sets of drivers, ensuring no overlap. • If concurrency is unavoidable, track which experiments each driver is part of and incorporate that as a factor in your analysis model. For example, add an indicator variable for “driver is in a concurrent incentive campaign.” This keeps partial confounding from overshadowing the effect of the UI.

If the A/B test shows no significant improvement, is there a systematic way to investigate “why” and possibly iterate on the new UI?

Finding a null result can be disheartening, but it is often a springboard for deeper inquiry:

• Review Logs And Clickstreams Check how drivers interact with the new UI. Maybe some elements are never clicked, or the new feature is hidden or misunderstood. Understanding usage patterns can reveal whether the UI design needs rearranging or better labeling.

• Check Feature Discovery If drivers claim they did not even notice the new capabilities, you might need more visible prompts or in-app messages to guide them.

• Run Follow-up Surveys Or Interviews A small set of qualitative interviews or a short survey inside the app can highlight pain points or confusion that is not obvious from raw data.

• Analyze Subgroups Even if the overall effect is null, specific subgroups might have positive or negative outcomes. That is a clue for focusing on those who actually benefit most.

• Iterate If the new UI was not significantly better, you can refine the design and test again. This might involve small adjustments (e.g., new color scheme for buttons, improved menu placement) or major conceptual changes (e.g., rethinking the entire workflow).

When re-running experiments, be mindful that repeated testing can inflate the chance of false positives or false negatives unless statistical techniques are adjusted for multiple comparisons and repeated experimentation.