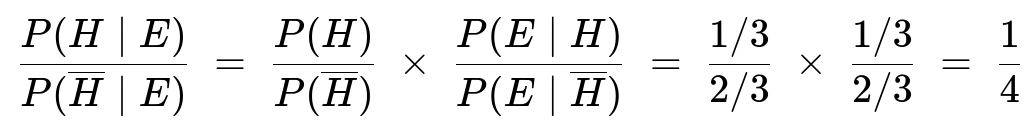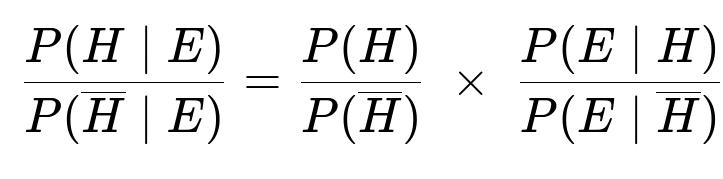ML Interview Q Series: Evaluating Statement Truthfulness with Bayesian Odds on the Island of Liars
Browse all the Probability Interview Questions here.
Question: On the island of liars each inhabitant lies with probability 2/3. You overhear an inhabitant making a statement. Next you ask another inhabitant whether the first inhabitant you overheard spoke truthfully. Using Bayes’ rule in odds form, find the probability that the first inhabitant indeed spoke truthfully given that the second inhabitant says so.
Short Compact solution
Let H be the event “the first inhabitant spoke truthfully.” Its prior probability is 1/3. Let E be the event “the second inhabitant says the first inhabitant spoke truthfully.” We apply Bayes’ rule in odds form:
Hence,
P(H ∣ E) = 1 / (1 + 4) = 1/5.
Comprehensive Explanation
Defining events and probabilities
We denote H as the event that the first inhabitant spoke the truth. Because inhabitants lie with probability 2/3, they tell the truth with probability 1/3. Therefore, P(H) = 1/3 and P(¬H) = 2/3.
We denote E as the event that the second inhabitant says, “Yes, the first one spoke truthfully.”
Conditional probabilities
To find P(E ∣ H), we ask: if the first inhabitant is indeed telling the truth, what is the chance the second inhabitant will say “Yes, he is telling the truth”? The second inhabitant must then be telling the truth about that fact, which occurs with probability 1/3. Hence P(E ∣ H) = 1/3.
To find P(E ∣ ¬H), we ask: if the first inhabitant is lying, what is the chance the second inhabitant will say “Yes, he is telling the truth”? The second inhabitant would then be lying about this situation (because in reality the first inhabitant is lying), and that lying happens with probability 2/3. Hence P(E ∣ ¬H) = 2/3.
Applying Bayes’ rule in odds form
The odds form of Bayes’ rule is often written as:
In our problem:
• P(H) = 1/3, so P(¬H) = 2/3 • P(E ∣ H) = 1/3 • P(E ∣ ¬H) = 2/3
Hence:
Converting odds to probability
When the odds for H versus ¬H are 1 : 4, it implies that H is only one part in a total of five parts:
P(H ∣ E) = 1 / (1 + 4) = 1/5.
Interpretation
Intuitively, even though the second inhabitant says the first is telling the truth, the second inhabitant’s own high lying probability (2/3) means the statement “Yes, he is truthful” is still very likely to be a lie—hence a relatively small posterior probability (1/5) that the first inhabitant truly was honest.
Potential Follow-up Questions and Detailed Answers
How would the result change if the lying probability were different?
If each inhabitant lied with a different probability, say p, then each inhabitant tells the truth with probability (1 – p). Denote that first inhabitant speaks truth with probability (1 – p) and the second inhabitant also has that same behavior. The calculation in odds form would be:
P(H) = 1 – p, and P(¬H) = p. Then P(E ∣ H) = 1 – p (the second inhabitant truthfully saying “Yes” if the first is truly correct), P(E ∣ ¬H) = p (the second inhabitant lying by saying “Yes” if the first is actually lying).
So the Bayes ratio becomes:
[(1 – p) / p] × [(1 – p) / p].
As p varies, the final posterior P(H ∣ E) would change accordingly. For instance, if p = 0.5, both inhabitants lie half the time, then the ratio would be [(0.5)/0.5] × [(0.5)/0.5] = 1 × 1 = 1, giving P(H ∣ E) = 1/2.
What if we asked multiple different inhabitants for confirmation?
If multiple independent inhabitants each confirm “Yes, the first inhabitant spoke truthfully,” we can multiply the likelihood factors for each additional inhabitant’s confirmation. Concretely, if n such independent inhabitants each claimed “Yes,” you would keep multiplying by P(E ∣ H) / P(E ∣ ¬H) for each new confirmation. The posterior probability that the first inhabitant was truthful would grow, reflecting the repeated confirmations—though you must assume independence of each additional inhabitant’s testimony, which may or may not be realistic in practice.
Why use odds form of Bayes’ rule here instead of the standard formula?
The odds form simplifies many ratio calculations. Specifically, you avoid having to compute P(E) = P(E ∣ H)P(H) + P(E ∣ ¬H)P(¬H) in the denominator. It is particularly convenient when you have to update prior odds by multiplying with a likelihood ratio, as seen in this question.
Does the content of the first inhabitant’s statement matter?
In this puzzle, it does not, because you are only evaluating whether the first inhabitant was truthful, not whether the content was actually correct or incorrect beyond that. The second inhabitant’s statement concerns the truthfulness of the first, not the actual proposition. For more complicated scenarios, you might have to consider the nature of the statement itself.
Could the first inhabitant’s actual lie/truth probability be different from the second inhabitant?
If the problem stated different lying probabilities for each inhabitant, you would have distinct probabilities for the second inhabitant’s reliability. The ratio approach still applies, but you would substitute the correct probabilities for each. The general pattern remains the same, but the numeric outcome changes to reflect the second inhabitant’s reliability.
These details show how Bayes’ rule in odds form is a practical tool for combining prior beliefs about truthfulness with newly observed testimony. By carefully enumerating the probabilities of truth and lies, we arrive at a posterior probability of 1/5 that the first statement was indeed truthful, even though the second inhabitant affirmed it.
Below are additional follow-up questions
What if there are more than two possible “answers” (e.g., the second inhabitant can say “not sure” or “partially true”)?
When the second inhabitant’s response is no longer a simple binary “the first one is truthful” vs. “the first one is lying,” you must expand your probability model to account for additional outcomes. Instead of working with two outcomes (Yes/No), you might have three or more possible answers, each with its own probability conditioned on whether the first inhabitant is telling the truth or not.
For instance, if the second inhabitant can say:
“Yes, it’s true,”
“No, it’s false,”
“I’m not sure,”
then you need to specify conditional probabilities: P(second inhabitant says “Yes” | first is truthful), P(second inhabitant says “No” | first is truthful), P(second inhabitant says “I’m not sure” | first is truthful), and the same for the case where the first inhabitant is lying. If each inhabitant is prone to lying 2/3 of the time, these outcomes would need to respect that lying probability in a consistent way—perhaps “I’m not sure” occurs if the second inhabitant tries to evade, or it could happen with some separate probability. After establishing these probabilities, you can use an extended version of Bayes’ rule (a more general form that sums over all possible ways the second inhabitant could respond) to find the posterior probability that the first inhabitant spoke truthfully.
A potential pitfall is incorrectly assigning probabilities to the “I’m not sure” or “partially true” statements. If you fail to clarify how lies and truths map to these extra statements, you can end up with ill-defined probability models, leading to incorrect results.
How does our solution change if the second inhabitant might not always answer your question?
If the second inhabitant can refuse to answer or remain silent, your evidence (E) may then be “the second inhabitant either responded affirmatively or not at all.” You have to define a new probability for the event that the second inhabitant chooses to respond. This additional layer means you’re conditioning not only on the truthfulness of the first statement but also on whether the second inhabitant decides to reply.
Formally, you might have:
P(E | H): probability that the second inhabitant both decides to respond and says “Yes” given the first inhabitant was truthful,
P(E | ¬H): probability that the second inhabitant both decides to respond and says “Yes” given the first inhabitant was lying,
P(no response | H) and P(no response | ¬H).
In practice, you would then apply Bayes’ rule incorporating these probabilities. A key pitfall here is mixing up the scenario where “no response” might be more likely if someone is lying versus if they are telling the truth. Without careful distinction, you could systematically bias your posterior and either overestimate or underestimate the probability that the first person was truthful.
Is there a possibility that the second inhabitant is biased or gains personal benefit from declaring the first inhabitant truthful?
In real-world or more nuanced logical puzzles, motivations and biases affect the probability model. If the second inhabitant benefits from saying “Yes, the first person is truthful,” they might do so more often than 1/3, even if they are “truthful” in some simpler sense. This scenario would require a model that includes incentives:
Perhaps the second inhabitant has a certain payoff for labeling statements as true or false.
We would then redefine P(E | H) and P(E | ¬H) in terms of that bias rather than a fixed “lie with 2/3 probability” alone.
A major pitfall is ignoring these biases or incorrectly thinking that “lies with probability 2/3” remains the entire story. In actual interviews or puzzle variants, the interviewer might test whether you realize that real agents can have motivations, and thus their “lying probability” is not purely random but strategic.
What if the two inhabitants are colluding or influenced by each other?
One of the assumptions in the standard solution is that the second inhabitant speaks (or lies) independently of the first inhabitant. But if the inhabitants can collude or share signals, then the second inhabitant’s statement might be coordinated with the first. For instance, if the first inhabitant says something false, the second inhabitant might be more likely to back them up, especially if they are collaborating for some reason.
Mathematically, we would no longer assume that P(E | H) = 1/3 independently. Instead, we would define a joint probability structure that captures collusion:
P(E | H, collusion) could be quite different from 1/3, maybe higher if the second inhabitant’s goal is to always support the first’s statement regardless of truth.
P(E | ¬H, collusion) might also differ drastically if they coordinate lies.
A classic pitfall is to overlook such correlation in their statements and still apply an independent Bayesian update. This leads to incorrect posteriors. In a real puzzle or scenario, you must check whether collusion or dependencies exist.
Could the inhabitants have prior knowledge or memory that influences their truthfulness?
If the inhabitants can recall previous interactions and tailor their truthfulness based on what has been said before, the probability that they lie might no longer be a fixed 2/3. For example, an inhabitant might habitually lie only about certain topics or might choose to tell the truth if lying before caused them trouble. That modifies the standard puzzle significantly:
The event H (first inhabitant is truthful) might be influenced by a “history of lying” or “time since last lie.”
The second inhabitant’s pronouncement about the first inhabitant could draw on past knowledge, possibly generating a conditional probability different from 1/3 or 2/3.
In such cases, you must either assume no memory or no strategic behavior. Failure to do so is a subtle pitfall that can cause your Bayesian model to over-simplify a complex situation.
What if you have partial observations about the second inhabitant’s past behavior?
Sometimes, you might have observed that the second inhabitant told the truth in earlier questions. This would update your belief about the second inhabitant’s reliability. If you now have reason to believe the second inhabitant’s probability of lying is different from 2/3 (perhaps you have a posterior distribution for the second inhabitant’s lying rate), you must incorporate that into P(E | H) and P(E | ¬H).
In an interview, explaining how you would handle partial or prior observations can be crucial:
You start with a prior belief that the second inhabitant lies with probability 2/3.
You observe them telling the truth multiple times in a row.
You update your belief, reducing your estimate of their lying probability.
You then recalculate the posterior about the first inhabitant’s truthfulness given the second inhabitant’s statement.
A pitfall is to treat 2/3 as an unchangeable fixed parameter despite contradictory repeated evidence from the second inhabitant’s behavior. In real probabilistic reasoning, consistency requires updating all relevant parameters in light of new data.
How does the puzzle work if we repeatedly ask the second inhabitant about the first statement in different ways?
If you can re-ask the second inhabitant the same question multiple times, you might be able to glean more information—unless you allow that the inhabitant’s responses in repeated queries can also be lies, potentially inconsistent across tries. With repeated queries, you could observe patterns (e.g., if the second inhabitant’s answers keep flipping). Then your Bayesian update becomes more complex:
Each new “Yes” or “No” is an additional piece of evidence that updates your prior.
Inhabitants might realize they need to remain consistent or might treat each question as an independent event to lie or tell truth.
A subtle pitfall is ignoring that repeated questioning can introduce psychological or logical constraints on the second inhabitant. If an inhabitant is rational, they might try not to contradict themselves across multiple answers, which introduces dependencies that a simple Bayesian framework (assuming independent statements) may fail to capture.
Can you extend this reasoning to evaluate the probability that both the first and second inhabitants are telling the truth?
In that more elaborate scenario, you would define a new event:
H1 = “the first inhabitant is truthful,”
H2 = “the second inhabitant is also truthful,”
and you might want P(H1 and H2 | E = “the second inhabitant says first is truthful”). You would factor in the second inhabitant’s statement about the first’s truthfulness, plus the second inhabitant’s truthfulness itself. A common approach is to note:
P(E | H1, H2) = 1 if the second inhabitant is truly truthful and acknowledges the first as truthful, P(E | H1, ¬H2) = 0 if the second inhabitant lies about the first’s truthfulness but the first is in fact telling the truth, etc.
You get a more complicated set of conditional probabilities. The pitfall arises when you forget the second inhabitant’s statement depends on H2 itself (whether the second inhabitant is lying or not), so you need a double-layered approach.
What if the first inhabitant’s statement is self-referential, such as “I am lying right now”?
Self-referential statements can create logical paradoxes (the “Liar’s Paradox”) that break classical probability models. If the first inhabitant’s statement is something that can’t be simply classified as “true” or “false,” then the entire premise “the first inhabitant spoke truthfully or not” becomes trickier to define. You could attempt to force a solution by assigning a conventional truth value to a paradoxical statement, but that usually undermines the puzzle’s consistency. The key pitfall is ignoring the logical paradox that certain statements cannot be consistently assigned a truth value. In an interview, it’s important to explain that standard Bayesian rules assume well-defined events (i.e., each proposition is either true or false, with definite probability), which is not always the case with self-referential statements.
Is the base rate of inhabitants on the island relevant in different contexts?
In some puzzles, the fraction of inhabitants who generally lie with a certain probability might differ. For instance, perhaps the island’s population is a mix of “always liars” and “always truth-tellers,” or a partial mixture of different lie probabilities. If an inhabitant is randomly picked from a population with various subgroups of different lying patterns, you might have to integrate over those subgroups to find the prior probability that any single inhabitant lies with probability 2/3. In other words, your prior P(H) might be an aggregate of multiple “inhabitant types.” A pitfall is to assume the entire island is homogeneous without verifying if that’s stated explicitly. Interviewers sometimes use such variations to test whether you can handle Bayesian mixing of multiple prior distributions.
Would the result change if you overheard the first inhabitant from a distance and there was a chance you misunderstood them?
In reality, “overhearing a statement” can introduce uncertainty about whether you heard it correctly. If there is some chance you misheard or misinterpreted that statement, your evidence about the first inhabitant’s truthfulness is partially noisy. You might need to assign a probability that your understanding of the statement is correct. Then you have a chain of conditional probabilities: the chance the statement is truly T or F, your chance of hearing T or F, and so on.
A pitfall arises when ignoring that your observation could be flawed. If the problem explicitly states you overheard them from a distance, you must incorporate that measurement uncertainty into the model. Otherwise, you inflate your confidence in the second inhabitant’s testimony about a statement that you might not have perfectly perceived in the first place.