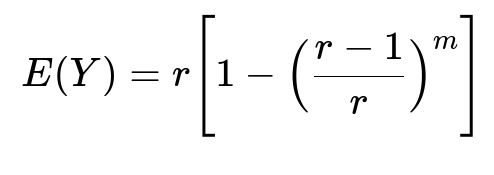ML Interview Q Series: Expectation and Deviation of Elevator Stops Using Indicator Random Variables
Browse all the Probability Interview Questions here.
A group of m people simultaneously enter an elevator at the ground floor. Each person randomly and independently chooses one of r floors (1,2,…,r) to exit. The elevator only stops on a floor if at least one person wants to exit on that floor. What are the expected value and the standard deviation of the number of stops the elevator will make?
Short Compact solution
Define Xj = 1 if nobody exits on floor j (so the elevator does not stop there) and 0 otherwise. Each person chooses a floor out of r floors uniformly and independently. Hence, P(Xj = 1) = ((r-1)/r)m.
The total number of floors that the elevator does not stop on is X = X1 + X2 + ... + Xr, so E(X) = r * ((r-1)/r)m.
The number of stops, call it Y, is r - X. Therefore, E(Y) = r - E(X) = r * [1 - ((r-1)/r)m].
For the variance, note E(Xj2) = E(Xj) since Xj is 0-1. Also, for j ≠ k, P(Xj = 1 and Xk = 1) = ((r-2)/r)m.
Thus,
E(X²) = r * ((r-1)/r)m + 2 * (r choose 2) * ((r-2)/r)m.
Then Var(X) = E(X²) – [E(X)]², and Var(Y) = Var(r - X) = Var(X). Consequently,
σ(Y) = √(Var(X)) = √(E(X²) – [E(X)]²).
Hence the expected value of the number of stops is r * [1 - ((r-1)/r)m], and its standard deviation is √(Var(X)) with Var(X) computed as above.
Comprehensive Explanation
Understanding the scenario
We have an elevator serving r floors above the ground floor. There are m passengers, each independently choosing exactly one of these r floors uniformly at random. The elevator will stop on any particular floor j (1 ≤ j ≤ r) if and only if at least one passenger has chosen that floor as their destination. We want the expected number of stops and the standard deviation of that number.
Defining a suitable random variable
To make the calculations more straightforward, define for each floor j a Bernoulli random variable Xj:
• Xj = 1 if floor j is not chosen by any of the m passengers (so the elevator will skip that floor). • Xj = 0 if at least one passenger chooses floor j (so the elevator will stop there).
Because each of the m people independently chooses from r floors with probability 1/r for each floor, the probability that nobody selects floor j is ((r-1)/r)m. Thus:
Xj has P(Xj = 1) = ((r-1)/r)m and P(Xj = 0) = 1 - ((r-1)/r)m.
Number of skipped floors
Let X = X1 + X2 + … + Xr. This quantity X is the total count of floors on which nobody gets off (i.e., no stop). By linearity of expectation:
E(X) = E(X1 + X2 + … + Xr) = r * ((r-1)/r)m.
Number of stops
The variable of interest is the number of floors at which the elevator does stop, call it Y. Notice that Y = r – X because the elevator either stops or does not stop on each of the r floors. Therefore,
E(Y) = r – E(X) = r * [1 - ((r-1)/r)m].
Second moment and variance
To find the standard deviation, we need Var(Y). But Var(Y) = Var(r – X) = Var(X). Hence we compute Var(X) by first finding E(X²).
Because X is the sum of the Xj, we use the expansion:
E(X²) = E( (Σj=1 to r Xj)² ) = Σj=1 to r E(Xj²) + 2 Σ1 ≤ j < k ≤ r E(XjXk).
Each Xj is 0-1, so Xj² = Xj. Hence E(Xj²) = E(Xj) = ((r-1)/r)m. For j ≠ k, XjXk = 1 only if nobody selects floor j and nobody selects floor k. Since each of the m passengers chooses a floor independently,
P(Xj = 1 and Xk = 1) = ((r-2)/r)m.
Thus,
E(X²) = r * ((r-1)/r)m + 2 * (r choose 2) * ((r-2)/r)m.
From that, Var(X) = E(X²) – [E(X)]². And since Var(Y) = Var(X), the standard deviation of Y is √(Var(X)).
Putting it all together
We summarize the expected value and standard deviation of the number of stops Y:
In other words, the number of stops is simply r minus the count of floors that are skipped (X). The probability a floor is skipped is ((r-1)/r)m, and we handle the standard deviation by considering pairwise independence properties for those Bernoulli indicators.
Practical insights
• If m is small relative to r, it becomes more likely that many floors are unselected, so the expected number of stops is smaller. • If m is large relative to r, then it is almost certain that every floor gets chosen, which pushes the expected number of stops close to r. • This model assumes each passenger chooses floors uniformly at random and independently from the others, which might not be realistic in real-world elevator usage, but it is a canonical assumption for a neat probability problem.
Implementation example
Here is a short Python snippet to empirically verify the result:
import random
import math
import statistics
def simulate_elevator_stops(r, m, trials=10_000_00):
counts = []
for _ in range(trials):
chosen_floors = [random.randint(1, r) for __ in range(m)]
# Number of distinct floors chosen
stops = len(set(chosen_floors))
counts.append(stops)
return statistics.mean(counts), statistics.pstdev(counts)
r = 5
m = 3
mean_stops, std_stops = simulate_elevator_stops(r, m)
print(f"Simulation: E(Y) ~ {mean_stops:.4f}, std(Y) ~ {std_stops:.4f}")
# Analytical values
import math
def expected_stops(r, m):
return r * (1 - ((r-1)/r)**m)
def std_stops(r, m):
p = ((r-1)/r)**m
q = ((r-2)/r)**m
eX = r * p
eX2 = r*p + 2*math.comb(r, 2)*q
varX = eX2 - eX**2
return math.sqrt(varX)
print("Analytical: E(Y) =", expected_stops(r,m), ", std(Y) =", std_stops(r,m))
This code checks the simulation results against the analytical formulas. Running it for large trials should show that empirical means and standard deviations approximate the derived formulas.
Potential Follow-up Questions
How does this result scale when r is very large and m is relatively small?
When r >> m, the probability that multiple passengers choose the same floor becomes smaller, so the floors chosen are more likely to be distinct. In this scenario, ((r-1)/r)m is close to 1 if m is small, so the expected number of stops may be near m if m < r (since you can’t have more distinct floors chosen than the number of passengers, in the limit where they rarely coincide). One might consider approximating for large r using a Poisson process viewpoint.
What if each person does not choose floors uniformly?
If passengers do not select floors with uniform probability 1/r, but with some other distribution, then the probability that a floor is selected by no one changes accordingly. Suppose each passenger chooses floor j with probability pj. Then P(Xj = 1) = (1 - pj)m. We would sum these probabilities over all floors to find E(X). Additionally, the pairwise probabilities P(Xj = 1 and Xk = 1) become (1 - pj - pk + pjpk)m if each person chooses j or k with probabilities pj or pk independently. The concept remains the same but the formulas must be adjusted.
Could you apply indicator random variables in another way to get the same result?
Yes. Instead of defining Xj as “no one picks floor j,” we could define Ij as “the elevator stops on floor j,” i.e., at least one person picks floor j. Then Ij = 1 with probability 1 - ((r-1)/r)m. Summing Ij over j directly gives the number of stops. The results for expectation and variance would match exactly.
What if we want the distribution, not just the mean and standard deviation?
To obtain the full distribution of the number of floors stopped at, we can observe that the number of stops is r minus the number of “empty” floors. The “empty” floors, X, follows a Poisson-binomial distribution because each floor’s “emptiness” is a Bernoulli random variable, but with certain correlations if we attempt to handle it differently. However, because each floor “emptiness” is identically distributed and we only track whether each passenger picks that floor or not, we can also use combinatorial arguments to find P(X = k), although it can be more complicated than just a closed-form expression for the distribution. Sometimes generating functions or inclusion-exclusion can help find an exact form.
How would you handle the case if the passengers do not choose floors independently?
The assumption of independence is crucial for the straightforward calculation P(Xj = 1) = ((r-1)/r)m. If the choices were correlated (e.g., certain floors always tend to be chosen together), we cannot simply multiply probabilities for j ≠ k. We would then need the joint distribution of passenger floor choices to compute P(Xj = 1 and Xk = 1), leading to more complex probability computations.
By examining these questions, one can see how the independence assumption and uniform probability distribution shape the elegance of the final result.
Below are additional follow-up questions
Could the distribution of the number of stops be approximated by a Poisson or a normal distribution in certain limiting cases?
A useful perspective is to consider asymptotic behavior when r (number of floors) and m (number of people) become large under different regimes:
Poisson Approximation (large r, relatively small m) If r is large and m is relatively small, the probability that two or more passengers choose the same floor can be low, so the number of distinct chosen floors may resemble the behavior of a Poisson process. Specifically, each floor being “unselected” has probability ((r-1)/r)^m ≈ exp(-m/r), and one can sometimes invoke a Poisson limit when m and r grow such that m/r remains roughly constant.
Normal Approximation (large m with comparable r) When both m and r are large enough, the distribution of the number of people choosing each individual floor (and hence the number of floors that get chosen at least once) can often be approximated by a normal distribution via a Central Limit Theorem–type argument, especially if p = 1/r remains constant. The sum of Bernoulli indicators X_j might become approximately normal as r grows large if the probabilities of emptiness or non-emptiness are not extreme.
However, the exact applicability depends on how r and m scale together. If m is extremely large compared to r, the probability of skipping a floor becomes very small, causing the number of stops to cluster near r. In that regime, a normal approximation might still hold for the fluctuation around the mean, but one has to examine whether boundary effects (e.g., saturating near r) are significant.
What happens in extreme edge cases like r = 1 or m = 1?
Case r = 1 There is only one floor above ground. If m ≥ 1, then that single floor is necessarily chosen by every passenger who wants to go anywhere (since there’s no alternative). The elevator will stop on that floor with probability 1. Hence the number of stops is always 1, and the standard deviation is 0.
Case m = 1 There is just one person. That person chooses uniformly among r floors. The number of stops is exactly 1 because the single person’s choice determines exactly one floor to stop on. The expected value of stops is 1, and the standard deviation is 0 as well, because there’s no randomness about how many floors get chosen once you know there is only one passenger and one floor choice.
These edge cases underscore how, at extremes, the distribution collapses to a degenerate scenario.
Can we incorporate a cost or time penalty for each stop to find an expected total travel time?
When analyzing real-world elevator performance, we might go beyond counting stops and consider the total time taken, which depends on how many floors are visited and in what order. Even if the order is fixed (say the elevator goes from floor 1 up to floor r), each stop adds a certain overhead (door opening, passenger exit, door closing, etc.). Let c be the average “stop overhead time,” and let t be the travel time per floor (moving from floor j to j+1). The expected total travel time T could be approximated as:
T ≈ (r – 1) * t + (expected number of stops) * c.
Here, (r – 1)*t is the time to travel sequentially through r floors. The random component is how many times we incur the overhead c. We already know the expected number of stops is r * [1 – ((r–1)/r)^m]. Hence:
E(T) = (r – 1)*t + c * r * [1 – ((r–1)/r)^m].
One subtlety: if no one selects a particular block of floors, there might be less travel time if the elevator could skip them entirely. In a simplified model where the elevator must pass all floors in numerical order anyway, this nuance vanishes. But if the elevator had “express skip” functionality, we would then need more complex computations for the travel time distribution.
How would we analyze the probability that the elevator stops at every floor (i.e., the event that all floors are chosen by at least one person)?
We can consider the event “all r floors are chosen.” This occurs if no floor is left out. The probability that a given set of k floors is chosen by nobody is straightforward, but for “all floors chosen,” we essentially want:
P(all floors chosen) = 1 – P(at least one floor is skipped).
A direct approach for “at least one floor is skipped” uses the complement or an inclusion-exclusion principle. The chance a specific floor j is skipped is ((r–1)/r)^m. But to find the probability that all r floors are chosen requires more advanced counting:
P(all floors chosen) = Σk=0..r ((–1)^k * (C(r, k)) * ((r–k)/r)^m ).
This is a direct application of the classical inclusion-exclusion formula for “no floor is left unchosen.” If r and m are large, one may approximate or bound this probability. Such a question highlights the link to the classic coupon collector setting.
Could there be a capacity limit on the elevator, and how would that affect the distribution?
If the elevator can carry at most n passengers with n < m, we can’t simply have all m people board at once. Instead, we might have multiple “batches” of people. Each batch could affect how many floors get chosen, and the elevator might return to the ground floor to pick up more passengers. This changes the problem fundamentally:
Batch 1 boards, chooses floors, elevator stops accordingly, and then returns.
Batch 2 boards, chooses floors, elevator stops accordingly, etc.
The total number of distinct floors across all batches might be greater than or equal to the number of stops in a single run if m > n. A thorough analysis would break down how each batch’s choices overlap. The expectation and variance become more involved because now each run is a separate random trial of floor selections, and the total number of distinct floors among all runs depends on the union of chosen floors. This scenario is more complex and requires us to track how many unique floors have been used across multiple elevator trips.
What if we allow the elevator to travel in both up and down directions?
In many real elevator systems, the order of visiting floors might not be simply 1 to r in ascending order. People can press buttons for different floors in a nonsequential manner, and the elevator’s control algorithm decides the route. For the count of stops, the order of visiting floors doesn’t matter; as long as a floor is selected by at least one passenger, it counts as 1 stop. So the distribution for the number of floors visited remains unchanged by the route.
However, if we were analyzing the exact time or distance traveled, then the route would matter significantly, leading to more complicated questions about optimizing elevator travel. In that scenario, you would move from counting floors to analyzing permutations of floor visits, or how an elevator’s scheduling algorithm impacts total travel time.
What if some floors have zero probability of being selected (e.g., restricted floors)?
Sometimes, certain floors might be off-limits or have a very small probability of being chosen. If a set of floors is effectively never selected, we can reduce the effective r to only those floors that can be chosen with nonzero probability. If floor j is “restricted,” we treat it as if pj = 0 for that floor. The distribution for the number of floors visited then only includes floors with nonzero pj. If the total “reachable” set of floors is r', then the same formula applies but with r replaced by r' and adjusting probabilities accordingly:
Probability no one chooses floor j is (1 – pj)^m.
We sum these or use an inclusion-exclusion approach if needed.
This highlights that the base approach remains the same, but we adjust for the fact that some floors might be impossible or improbable to choose.
How could we construct confidence intervals or concentration bounds for the number of stops?
A practical question is: “What is the probability that the number of stops deviates significantly from its mean?” We can use tools like Chernoff bounds or Hoeffding’s inequality. For instance, let Y = number of stops. Recall Y = Σj=1..r (1 – Xj), where Xj = 1 if floor j is not chosen. One might apply a Chernoff bound to the sum of Bernoulli random variables Ij = 1 – Xj:
E(Ij) = 1 – ((r–1)/r)^m.
The Ij can be treated as independent if we approximate or ignore small correlations (strict independence does not hold exactly if we sum “no one chooses floor j,” but in many practical approximations, it’s used anyway).
Then for large r, we might write:
P(|Y – E(Y)| ≥ δ E(Y)) ≤ 2 exp(–E(Y) * f(δ)),
where f(δ) is some function derived from Chernoff bounds. This would give a probabilistic guarantee on how the actual number of stops concentrates around its mean. The exact shape of these bounds depends on the correlation between floors. But for large r with small (r–1)/r, these correlations may be fairly manageable, giving a useful approximate confidence interval.