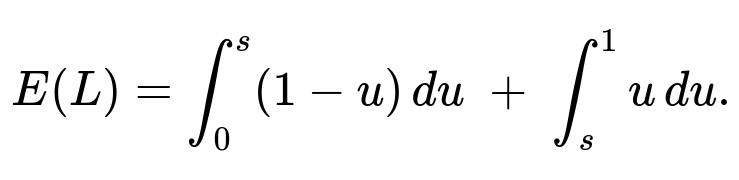ML Interview Q Series: Expected Length of Random Covering Subinterval: Solved with Integration

Browse all the Probability Interview Questions here.

10E-14. Choosing at random a point in (0,1) divides this interval into two subintervals. What is the expected value of the subinterval covering a given point s with 0 < s < 1?

Short Compact solution

Consider a random point U chosen uniformly in (0,1). If U < s, then the subinterval that covers s is (U,1) of length 1 - U, while if U ≥ s, it is (0,U) of length U. Thus, the length L of the subinterval covering s is given by g(U) = 1 - U for U < s, and g(U) = U for U ≥ s. The expected length E(L) is then

[ \huge \text{(in integral form) } \int_{0}^{s} (1-u),du + \int_{s}^{1} u,du ,=; s ;-; s^2 ;+; \tfrac{1}{2}. ]

Hence the final expected value of the covering subinterval’s length is s - s^2 + 1/2.

Comprehensive Explanation

Setup and Definition of the Random Variable

We have an interval (0,1) and a point s with 0 < s < 1. We randomly choose another point U in (0,1), with U uniformly distributed. This random choice splits (0,1) into two subintervals:

• (0,U) has length U • (U,1) has length 1 - U

We then look at which subinterval contains s. Two cases arise:

1. If U < s, then s lies in (U,1). The length of that subinterval is 1 - U.

2. If U ≥ s, then s lies in (0,U). The length of that subinterval is U.

Hence, we define a function g(U) that represents the length of the subinterval containing s:

• g(U) = 1 - U if U < s

• g(U) = U if U ≥ s

Because U is uniform on (0,1), its probability density function f(U) = 1 for all 0 < U < 1.

Expected Value Calculation

We want E(L), the expected value of L = g(U). By definition of expectation for a continuous random variable:

Since f(u) = 1 on (0,1), we split the integral at the point u = s:

We evaluate each integral separately:

• For 0 ≤ u ≤ s, we integrate 1 - u: ∫(1 - u) du from 0 to s = [u - u^2/2]_0^s = s - s^2/2

• For s ≤ u ≤ 1, we integrate u: ∫u du from s to 1 = [u^2/2]_s^1 = (1/2) - (s^2/2)

Summing these results:

(s - s^2/2) + (1/2 - s^2/2) = s - s^2 + 1/2.

Hence,

Interpretation and Key Observations

• When s is close to 0, the random point U is quite likely to be above s, so the length tends to be U on most draws. In that scenario, we expect L to be somewhat near 1/2 on average, but slightly influenced by s. • When s is close to 1, the random point U is more often below s, so the length tends to be 1 - U on most draws. Again, the expected length is around 1/2, modified by s. • The result s - s^2 + 1/2 can also be rearranged as 1/2 + s(1 - s). This shows how s influences the mean in a quadratic manner.

Possible Pitfalls

• Mixing up which subinterval is chosen in each case can lead to reversing the integral limits. You must ensure the subinterval containing s is the correct one based on the condition U < s or U ≥ s. • Forgetting that the random point U is uniform in (0,1) would alter the density function f(u). With any other distribution, we would have to weight g(U) by that distribution.

Follow-Up Questions

How could we verify the result using an alternative approach?

One alternative is to consider the random variable L directly in a piecewise manner and use the law of total expectation:

E(L) = E(L | U < s)P(U < s) + E(L | U ≥ s)P(U ≥ s).

Because U is uniform(0,1), P(U < s) = s and P(U ≥ s) = 1 - s. Then:

• If U < s, L = 1 - U, so E(L | U < s) = 1 - E(U | U < s). Under uniform(0,1), conditioned on U < s, U is uniform(0,s) and E(U | U < s) = s/2. Thus E(L | U < s) = 1 - (s/2). • If U ≥ s, L = U, so E(L | U ≥ s) = E(U | U ≥ s) = (s + 1)/2 under uniform(0,1).

Multiply each by the respective probabilities s and 1 - s and sum to get the same final E(L) = s - s^2 + 1/2.

What happens if s = 0 or s = 1?

Technically, the question states 0 < s < 1. But if s were exactly 0, then any random point U > 0 would place s in (0,U). That would effectively lead to L = U almost always. Similarly, if s were 1, then s would lie in (U,1) if U < 1. In either degenerate case, the formula s - s^2 + 1/2 yields 1/2 for s=0 or s=1, which matches the intuitive idea that the expected subinterval length is about 1/2 on average when one endpoint is pinned down.

Could we simulate this in Python to confirm?

Yes. A quick Monte Carlo simulation can verify the analytical result:

import numpy as np

def expected_covering_subinterval_length(s, trials=10_000_000):
    U = np.random.rand(trials)  # uniform in [0,1)
    lengths = np.where(U < s, 1 - U, U)
    return lengths.mean()

# Example usage:
s_value = 0.3
estimate = expected_covering_subinterval_length(s_value)
theoretical = s_value - s_value**2 + 0.5
print("Simulation:", estimate)
print("Theoretical:", theoretical)

Running this simulation for large trials will show results converging toward the theoretical value s - s^2 + 1/2.

What if we had a non-uniform distribution for U?

If U had some density function f(u) on (0,1) different from the constant 1, the expectation would become:

E(L) = ∫ g(u) f(u) du.

But we would no longer have a simple split of probabilities s and 1 - s for U < s and U ≥ s. Instead, we would need to integrate with the appropriate weights given by f(u). The approach remains conceptually the same: define the piecewise function for L depending on u relative to s, and integrate over those regions with the correct density.

Are there geometric interpretations or intuitive explanations?

An intuitive approach is to imagine randomly picking a point U in (0,1). The chance that U lands to the left of s is exactly s. So for s fraction of the time, the covering subinterval is 1 - U, and for the remaining fraction of time (1 - s), the covering subinterval is U. Integrating or taking a conditional expectation in each region gives the same final expression. This geometric viewpoint helps confirm that s - s^2 + 1/2 is consistent, since the result transitions smoothly from s=0 to s=1, and achieves a maximum near s=1/2 (symmetry considerations also suggest an approximate half-length on average).

All these perspectives underscore the same conclusion:

Below are additional follow-up questions

How can we compute the variance of the subinterval length L?

To calculate the variance, we need both E(L) and E(L²). We already know E(L) = s - s² + 1/2. Let’s find E(L²).

Recall that L = 1 - U if U < s, and L = U if U ≥ s. Hence,

E(L²) = ∫[0 to s] (1 - u)² du + ∫[s to 1] u² du.

Compute each part:

1. ∫(1 - u)² du from 0 to s:

(1 - u)² = 1 - 2u + u². So, ∫(1 - 2u + u²) du from 0 to s = [u - u² + (u³/3)] from 0 to s = (s - s² + s³/3).

2. ∫u² du from s to 1:

∫(u²) du from s to 1 = [u³/3] from s to 1 = (1/3 - s³/3).

Summing these:

E(L²) = (s - s² + s³/3) + (1/3 - s³/3) = s - s² + 1/3.

Given that Var(L) = E(L²) - [E(L)]², we substitute E(L) = s - s² + 1/2 and E(L²) = s - s² + 1/3:

• [E(L)]² = (s - s² + 1/2)² = s² - 2s³ + s^4 + s - s² + 1/4 (expand carefully) • Then Var(L) = (s - s² + 1/3) - (s - s² + 1/2)².

Because expansions can be tricky, let’s do it systematically:

(E(L)) = s - s² + 0.5 (E(L))² = (s - s² + 0.5) * (s - s² + 0.5).

You can expand term-by-term:

• s * s = s²

• s * (-s²) = -s³

• s * 0.5 = 0.5 s

• (-s²) * s = -s³

• (-s²) * (-s²) = s^4

• (-s²) * 0.5 = -0.5 s²

• 0.5 * s = 0.5 s

• 0.5 * (-s²) = -0.5 s²

• 0.5 * 0.5 = 0.25

Summing up:

s² - 2s³ + s^4 + s + (-s²) + 0.25 = s^4 - 2s³ + (s² - s²) + s + 0.25 = s^4 - 2s³ + s + 0.25.

So:

[E(L)]² = s^4 - 2s³ + s + 0.25.

Finally:

Var(L) = [s - s² + 1/3] - [s^4 - 2s³ + s + 0.25].

We can leave this expression in factored or expanded form depending on preference. While it looks a bit complicated, we can always rely on a symbolic manipulation tool or do the algebra carefully by hand. The key takeaway: you can compute the variance directly by piecewise integration and subtracting the square of the mean.

What if we want the distribution function of L?

We know L depends on the position of U relative to s. Let’s define L’s cumulative distribution function (CDF) F_L(x) = P(L ≤ x).

When U < s, L = 1 - U, so L ranges from 1 - s down to nearly 0 (if U is close to s, L is close to 1 - s; if U is close to 1, that scenario is not possible because we restricted U < s). When U ≥ s, L = U, so L ranges from s to 1.

We can tackle it in a piecewise way:

• For x < 0, F_L(x) = 0 because L ≥ 0. • For 0 ≤ x < s, L = U can only be less than x if U < x, but we must also have U ≥ s in that part. That means no U in [s,1] can be < x if x < s. So in this region, only the (1 - U) segment might yield a value ≤ x. We solve 1 - U ≤ x → U ≥ 1 - x. Because U < s, we need 1 - x ≤ U < s. We also need 1 - x ≤ s for this region to make sense. In other words, if x < 1 - s, that region might not apply. • For s ≤ x ≤ 1, we have additional contributions from the U≥s part, and so on.

Because this can be slightly intricate, a simpler path is to find the distribution by noting L can’t exceed max(1 - s, s), and L can’t go below min(1 - s, s). The distribution is constructed from merging the random variable (1 - U) for U < s and the random variable U for U ≥ s. This yields a mixture distribution with weight s on the random variable (1 - U over [0,s]) and weight 1 - s on the random variable U over [s,1]. By analyzing these two sub-variables separately, each uniform in its sub-interval, we can carefully piece together the entire distribution for L.

If we select two random points independently in (0,1), does it affect the expected covering length for s?

When we select one point U in (0,1), the subinterval covering s is well-defined as before. If we pick a second point V independently in (0,1), it doesn’t change which subinterval covers s, because that determination depends only on U’s position relative to s. The presence of V is irrelevant for the single subinterval containing s. The random variable L = length of the subinterval containing s still has the same distribution, and E(L) remains s - s^2 + 1/2. Unless we specifically define a new procedure that uses both U and V (for example, picking the subinterval that is also to the left of V or something more complicated), the second point doesn’t affect the original question.

In practice, confusion might arise if we somehow compare the subinterval from U to the subinterval from V. But as stated, the subinterval containing s is chosen only by U’s position relative to s. So the expectation result remains unchanged.

What if we define a variant of the problem where we always pick the “other” subinterval that does NOT contain s?

Sometimes you might consider the complementary subinterval: If U < s, the subinterval covering s is (U,1), but we decide to measure the other subinterval (0,U). If U ≥ s, the subinterval covering s is (0,U), but we measure (U,1). This effectively makes L' = U if U < s, and L' = 1 - U if U ≥ s. Notice that this new L' is precisely 1 - L from the original problem.

Because E(1 - L) = 1 - E(L), we get:

E(L') = 1 - [s - s^2 + 1/2] = 1/2 + s^2 - s.

So the complementary subinterval’s average length is 1/2 + s^2 - s, which is a symmetric result that might be useful if the question were about the subinterval that does not contain s.

Could s itself be considered a random variable?

Yes, sometimes s is also random, uniformly drawn from (0,1). In that case, both s and U are random. We would need to consider the joint distribution of (s, U). If s and U are independent and uniform, the subinterval that contains s might have an expectation computed by integrating over all s. One approach:

• Condition on s, compute E(L | s) = s - s^2 + 1/2. • Then average over the distribution of s, which is uniform on (0,1).

Hence, E(L) = ∫[0 to 1] [s - s^2 + 1/2] ds. Evaluate:

∫(s - s^2 + 1/2) ds from 0 to 1 = [s²/2 - s³/3 + s/2]_0^1 = (1/2 - 1/3 + 1/2) = 1 - 1/3 = 2/3.

So if s is uniform on (0,1), the average expected covering length over all possible s is 2/3.

In real-world use cases, how would floating-point precision affect the simulation or the integral?

When you do a large-scale simulation in Python or another language, floating-point issues can come into play. For instance:

• If s is extremely close to 0, floating-point round-off might make certain computations tricky when s is on the order of 1e-15. • Summations in a loop might accumulate floating-point errors if not carefully handled.

However, for moderate values of s (like 0.3 or 0.7) and a typical double-precision floating-point environment, the simulation will be quite accurate for computing E(L). The main way to mitigate floating-point pitfalls is to use robust data types (double precision in Python’s NumPy is generally good enough), or use techniques like Kahan summation if dealing with sums of many random draws. But for a straightforward integral approach or a million-sample simulation, the standard double precision is typically sufficient to get you very near the theoretical result.

How does conditioning on event sets like U < s and U > s help ensure correctness?

A subtle pitfall is forgetting to multiply by P(U < s) or P(U ≥ s) when using conditioning. For example, you might see an incorrect approach where someone writes E(L) = E(1 - U) + E(U) without weighting them by the probabilities that each sub-event occurs. The correct approach uses:

E(L) = E(L | U < s)P(U < s) + E(L | U ≥ s)P(U ≥ s).

Since P(U < s) = s and P(U ≥ s) = 1 - s for a uniform(0,1) variable U, ignoring these factors leads to an incorrect result. Always ensure that your partial expectations are weighed by the appropriate sub-probabilities in such conditional partitions.