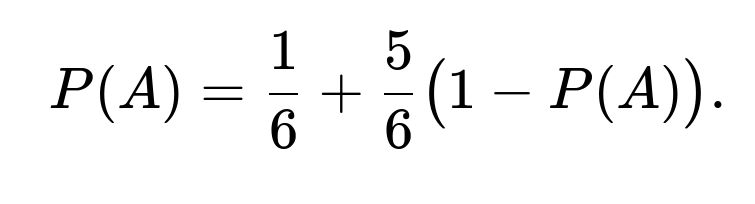ML Interview Q Series: Expected Value and Recursion: Valuing the First Roll in a Probabilistic Dice Game.
Browse all the Probability Interview Questions here.
A game involves selecting one face from a six-sided die, and then two players, A and B, alternate rolling the die. The first player to roll the chosen face earns \$100. Determine how much A should pay to secure the right to roll first.
Short Compact solution
If we let P(A) be the probability that A wins when rolling first, we can analyze it as follows. On A’s opening roll, there is a 1/6 chance of rolling the winning face immediately. If A does not roll the winning face (which happens with probability 5/6), then B is effectively in the same position A was at the start, just with B going first. By symmetry, if B goes first, the probability that B eventually wins matches P(A), so A’s chance of winning in that scenario is 1−P(A). Thus, we set up the equation
Comprehensive Explanation
The core idea of the problem is to compute how often A will roll the chosen face before B when A begins the game. Because each player rolls the same fair six-sided die, each attempt has a 1/6 chance of success on any given roll and a 5/6 chance of not matching the chosen face.
A crucial insight is that once A fails to roll the winning face, the roles of the players reverse for the remainder of the game: B becomes the “first” roller for the subsequent tosses, and the problem remains identical in structure. This symmetry allows us to write a straightforward recursion for P(A), the probability that A wins starting first.
When A starts:
There is an immediate 1/6 probability of rolling the winning face on the first try.
There is a 5/6 probability A misses on the first roll. If that happens, then B faces the exact same odds that A initially did, but with B in the “first” position. Hence B’s probability of winning from this point on is P(A) (by symmetry), so A’s probability of eventually winning if A’s first roll is not successful is (1−P(A)).
Putting this all together in an equation:
The left side P(A) is the total probability that A eventually wins. On the right side, we break it down into “winning on the first roll with probability 1/6” plus “missing on the first roll with probability 5/6” and then winning after B fails (which has probability 1−P(A), because B has probability P(A) of winning in that reversed position).
Rearranging:
[
\huge P(A) = \frac{1}{6} + \frac{5}{6}\bigl(1 - P(A)\bigr) = \frac{1}{6} + \frac{5}{6} - \frac{5}{6} , P(A). ]
Bringing terms involving P(A) together:
[
\huge P(A) + \frac{5}{6} , P(A) = \frac{1}{6} + \frac{5}{6} \quad\Longrightarrow\quad \frac{11}{6},P(A) = 1 \quad\Longrightarrow\quad P(A) = \frac{6}{11}. ]
Thus, if A goes first, A wins with probability 6/11. By symmetry, if B goes first, B would win with probability 6/11, so in that case A’s winning probability would be 5/11.
[ \huge \bigl(100 \times \tfrac{6}{11}\bigr) ;-; \bigl(100 \times \tfrac{5}{11}\bigr)
100 \times \bigl(\tfrac{6}{11} - \tfrac{5}{11}\bigr)
\frac{100}{11}. ]
That corresponds to approximately $9.09. Hence, $9.09 is the maximum amount A should pay to secure the first roll, because paying any more would make the net expected profit negative.
Follow-up question: Why does symmetry imply that P(B′)=P(A)?
Symmetry here means that once A fails the first roll, the roles are simply reversed with B now in the “first player” position. The structure of the game is otherwise unchanged: the die has not lost or gained any special properties, and the chosen face remains the same. Therefore, the probability that B eventually wins from that point forward is exactly the same as the probability that A would win if A had been the first player at the start of a fresh game. This is why we label B’s probability of winning after A’s initial miss as P(A), leading to A’s probability of winning in that scenario as 1−P(A).
Follow-up question: What if the die is not fair?
[
\huge P(A) = p_k + (1 - p_k)\bigl(1 - P(A)\bigr) = p_k + (1 - p_k) - (1 - p_k),P(A). ]
We collect terms involving P(A):
[
\huge P(A) + (1 - p_k),P(A) = p_k + (1 - p_k) \quad\Longrightarrow\quad P(A)\bigl[1 + (1 - p_k)\bigr] = 1 \quad\Longrightarrow\quad P(A) = \frac{1}{1 + (1 - p_k)} = \frac{1}{2 - p_k}. ]
Follow-up question: What if the payout is different from $100?
If the prize is some other amount, say $C, the probability calculations for P(A) and P(B) remain unchanged. The only difference is that the expected monetary outcome is scaled by the factor C instead of 100. Since the advantage difference is C×(P(A)−P(B)), and P(A)−P(B)=1/11 under the fair-die scenario, the exact amount one should pay to go first is
[ \huge \text{Cost to go first} = C \times \frac{1}{11}. ]
For example, if C=200, the cost to go first would be $200 \times (1/11) = 200/11 \approx 18.18.
Follow-up question: Can we simulate this game programmatically?
Yes, we can easily write a Python simulation using random numbers to approximate these probabilities and validate our theoretical solution. Below is a brief illustration:
import random
def simulate_game(num_simulations=10_000_000):
count_A_wins = 0
for _ in range(num_simulations):
chosen_face = random.randint(1, 6)
# A goes first
turn = 'A'
while True:
roll = random.randint(1, 6)
if roll == chosen_face:
if turn == 'A':
count_A_wins += 1
break
turn = 'B' if turn == 'A' else 'A'
return count_A_wins / num_simulations
prob_A_wins = simulate_game()
print(f"A's estimated win probability: {prob_A_wins:.4f}")
In this simulation:
We choose the winning face uniformly from {1,...,6}.
We alternate rolls until one player hits the chosen face.
We track how often A wins out of many trials to estimate P(A).
As the number of simulations grows large, we should see P(A) approach 6/11.
Follow-up question: How can we extend this logic to an n-sided die?
If there are n sides, the chosen face has probability 1/n of appearing on any roll. The same recursion approach applies: if A goes first, then
Solving similarly for P(A),
[
\huge P(A) + \frac{n-1}{n} P(A) = \frac{1}{n} + \frac{n-1}{n} \quad\Longrightarrow\quad \frac{2n-1}{n},P(A) = 1 \quad\Longrightarrow\quad P(A) = \frac{n}{2n-1}. ]
Follow-up question: How does risk aversion or repeated play change the analysis?
In this idealized puzzle, we assume that both players are risk-neutral and are content to value outcomes by their expected monetary return. In practical settings, an individual might be risk-averse and might value the guarantee of a smaller sure amount more than a random payout with the same expectation but higher variance. That would complicate the question of how much one would “pay” to go first.
Repeated play could also alter the value of going first because players might have the opportunity to offset or hedge previous losses in subsequent rounds. However, from a purely expected-value perspective, each round of the game remains the same analysis, and the advantage to the first player does not change for each new round. It is only aggregated over multiple rounds.
All in all, under standard assumptions (fair die, risk-neutral players, single play of the game), the difference in expected value between going first or second is $100/11 \approx $9.09, which is exactly how much A should be willing to pay for the privilege of rolling first.
Below are additional follow-up questions
Follow-up question: What if the chosen face changes partway through the game?
One interesting twist occurs if, after a certain number of rolls (or at a random moment), the chosen face k switches to some other face k′. This sudden change affects the win probabilities in a non-trivial way.
Analysis
Initial Phase: Before the face changes, the game proceeds exactly as in the original scenario. For instance, if A starts, A’s probability of winning up to the moment of change is still 6/11 in the fair six-sided case (or some analogous formula if it’s not fair or if there are more sides).
Moment of Change: Once the face switches to k′, we must consider:
Has either player already won by rolling the original k? If yes, the game ends immediately (the switch never comes into play).
If the change happens during the middle of a turn, we would need to define how that transition works. Do we finish the current roll with k still in effect, or does k′ take over at once?
Post-Change Dynamics: After the face changes, the probabilities effectively reset to a “new” game with k′ as the target face, and we must figure out who rolls first in that new sub-game. If a switch is scheduled (say after m total rolls), then whichever player’s turn comes immediately after roll number m has the advantage akin to being the “first mover” for the new face k′.
Impact on Strategy: If players know the switch is coming, the current player might try to maximize rolls prior to the switch if the current target k is easier or less favorable, and possibly stall or rush. While stalling is generally not an option in a traditional dice-roll game, any dynamic that lets a player choose whether to roll now or later (such as a time-based mechanism) could be exploited.
Potential Pitfalls
Mid-Roll Ambiguity: If the chosen face changes mid-roll, the players need clear rules about whether the just-rolled value is counted toward the old face or the new one. Failing to define this leads to disputes about who actually wins at the moment of transition.
Overlapping Conditions: If the game is repeated multiple times and the face changes in each sub-game, careful tracking of which face is currently in effect is essential.
In sum, the probability of A or B winning can still be computed piecewise, but it requires careful breakdown of the time intervals (or number of rolls) under each target face. The final formula is more involved than the simple 6/11, since we stitch together multiple scenarios before and after the change.
Follow-up question: What if each roll incurs a penalty or cost?
Another variant is where each roll has a fixed cost, say $1 per throw, deducted from the eventual winner’s prize. This means even if you win, you pay for all the attempts, which changes the expected value.
Analysis
Basic Setup: Assume the cost of each roll is $1 and the prize remains $100 for the first player who hits the chosen face.
Expected Number of Rolls: The game is a geometric process with a success probability of 1/6 on any given roll (in the fair six-sided case). The expected number of total rolls until one success is 1/(1/6)=6 in the simplest scenario. But the distribution can vary, and sometimes it could take many more rolls than the mean.
Who Pays the Costs?: Typically, in such a variant, the winner is the only one who receives the prize minus all incurred costs. If the total cost for r rolls is $r, then the net payout is $$(100 - r).
If you know the expected length of the game, you might try to factor that into whether it’s still worth paying for the privilege of going first.
A going first might accelerate the end of the game slightly because A has an immediate opportunity to succeed, which in turn affects how many rolls on average the game will last.
Computation: The expected number of rolls can be split between A and B. If A goes first, there’s a 1/6 chance the game ends on the very first roll, incurring only $1 in cost. However, if the game continues longer, more cost accumulates. Estimating the total cost paid by the eventual winner requires summing over all possible times to success, weighted by the probability that A (or B) wins on that specific roll.
Potential Pitfalls
Unequal Sharing of Costs: If the game design is that each player pays for their own rolls rather than deducting from the final winner, that changes the net value to each player. The typical approach is that the winner pays for all rolls, but different interpretations lead to different calculations.
Overall, to determine how much A should pay to move first, one would compute A’s net expected value, factoring in the expected total cost of rolls. That adjusted expected value must be balanced against the situation where A doesn’t go first.
Follow-up question: What if there is a maximum number of rolls allowed?
Sometimes a game design might impose a cap—for example, “We only allow 10 total rolls; if no one hits the face by then, no one gets paid.” This changes the probabilities because the game may end without a winner.
Analysis
Truncation of the Process: If there are at most R rolls, then the probability that someone hits the chosen face within R rolls depends on the usual geometric distribution but truncated at roll R.
Turn Sequence: If R is even, each player gets exactly R/2 rolls if the game lasts that long. If R is odd, the first player (A) would get ⌈R/2⌉ rolls, while the second player (B) gets ⌊R/2⌋ rolls.
Expected Value Computation: The final chance that A wins is the sum over the probabilities that A rolls the winning face on each of A’s allotted turns, minus the probability that the game ended on a previous roll by either player.
Potential Pitfalls
Edge Cases:
If R=1, A only has a single roll, and if it fails, no one wins. In that scenario, P(A)=1/6 and P(B)=0, which significantly changes the usual result.
If R is large (much larger than the typical geometric waiting time), the truncated scenario is almost the same as the infinite case, so P(A)≈6/11.
Strategic Considerations: If we imagine a scenario in which a player could “skip” to preserve an attempt for later, the logic would become more complicated. Typically, dice games do not allow skipping a turn, so each turn is forced until the maximum roll count is reached.
Truncating the process introduces a higher chance that no one wins, thus reducing the expected value of the entire game. A would pay less to go first if there’s a decent chance the prize will never be awarded.
Follow-up question: What if the first player can “pass” the initial roll?
If the rules allow a player who has the turn to decide whether to roll now or pass (thus relinquishing the turn to the opponent), some strategic complexity arises. For instance, a risk-averse or risk-seeking player might skip certain opportunities to roll.
Analysis
Motivation to Pass? Typically, you wouldn’t want to pass an immediate chance at rolling the chosen face when the success probability is 1/6 each time. On average, having a turn is an advantage. However, if there are external factors—such as costs per roll or if the chosen face might change to something more favorable in the future—passing might have strategic merit.
Infinite Loop Risk: If both players decide passing is advantageous, the game rules need to forbid an endless sequence of passes. Possibly a pass-limit or a penalty for passing could be in place.
Computational Strategy:
If passing is free and there’s no penalty, it’s almost always better to take your roll rather than hand the turn to your opponent.
If a penalty or some future advantage is known, the decision becomes a dynamic programming problem: for each state (which player’s turn it is, how many rolls remain, or whether the face might change), you compare the expected value from rolling now vs. passing.
Potential Pitfalls
Counterintuitive Scenarios: The mere introduction of a “pass” option with no penalty usually leads to no rational passing—since each roll is an independent chance to win at probability 1/6. But if the game has complicated expansions (like the chosen face changing soon or cost structure changes), a pass could momentarily become optimal.
Misapplication of Basic Probability: A naive player might think “I’ll wait until I have a ‘better chance’,” but if the die is fair and the target face is fixed, that “better chance” never comes since each roll is still 1/6.
Hence, in most simple forms of the game, the pass option yields no advantage, so the question of how much A should pay to go first remains the same as in the original analysis.
Follow-up question: What if the game is repeated multiple times with cumulative scoring?
In a tournament-style version, the game might be repeated M times, and each time a player wins, they earn $100. At the end, each player’s total is computed. We can ask how the advantage of going first accumulates across multiple plays.
Analysis
Independent Rounds: If each round is reset with a fair six-sided die and a newly chosen face, each round is effectively the same as the original single-round scenario. If the same player (A) always goes first in each round, then each round gives A an advantage of 6/11−5/11=1/11 in winning probability for that round. Over MM rounds, the expected difference in the number of wins is (1/11)×M in A’s favor.
Changing Who Goes First: If the rule states that the loser of the previous round goes first in the next round, the advantage can shift from round to round. Then we would need to track the probability of transitions between “A goes first” and “B goes first” states.
Potential Pitfalls
Limited Memory: If after each round the turn order does not automatically switch, you get a consistent advantage to the same starter, drastically favoring that player over many rounds.
Adaptive Strategies: In repeated play, a losing player might demand to shift who goes first in the next round to maintain fairness, or else they may walk away. If the game design specifically states a fixed order, it can lead to a large disparity in total earnings after multiple rounds.
Follow-up question: What if the die’s fairness (or bias) is only partially known?
Players might suspect the die is biased, but not know the exact probabilities of each face. They might try to infer it from observed rolls in the current or previous games.
Analysis