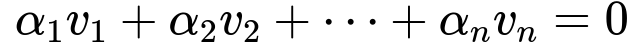ML Interview Q Series: Explain how the span of a set of vectors is defined and elaborate on the concept of linear dependence.
📚 Browse the full ML Interview series here.
Comprehensive Explanation
The span of a set of vectors in a vector space is the set of all possible linear combinations of those vectors. When we say a vector x lies in the span of a collection of vectors, we mean there is some way to combine these vectors (via scalar multiplication and addition) to produce x. It is a fundamental notion because it describes how vectors can generate or “cover” a particular subspace.
The concept of linear dependence arises when one vector in the set can be expressed as a linear combination of the others. If there is no such nontrivial combination that yields the zero vector (other than using all scalar coefficients equal to zero), the set of vectors is said to be linearly independent. If at least one vector can be expressed in terms of the rest, they are linearly dependent.
These ideas are crucial in linear algebra because they help define bases, dimensions of subspaces, and rank in matrices. They also have deep applications in machine learning and data science, such as feature space construction, dimensionality reduction, and understanding the geometry of data embeddings.
Span Definition and Notation
One formal way to define the span of vectors v1, v2, …, vn in a vector space is to consider every possible linear combination of these vectors. The core formula for the span is often written as
Here, v1, v2, …, vn are vectors in a given vector space (for example, R^d). The scalars alpha_1, alpha_2, …, alpha_n are real numbers (or elements of some underlying field like R or C), and a linear combination refers to summing each vector scaled by its corresponding coefficient.
A subspace can be described by the span of a set of vectors if all of its elements can be formed as linear combinations of those vectors. This is why we say these vectors “span” that subspace.
Linear Dependence
A collection of vectors is linearly dependent if there is a nontrivial way to write the zero vector as a linear combination of these vectors. In other words, there exists a set of scalars (not all zero) that, when used to scale these vectors and then add them together, give the zero vector. Formally, the condition for linear dependence can be written as
where at least one alpha_i is nonzero. If the only solution to this equation is alpha_1 = alpha_2 = … = alpha_n = 0, then the vectors are linearly independent.
In practical terms, linear dependence means at least one vector in the set is redundant in describing the span; you can remove it without reducing the span of the set. Linear independence ensures the set is as “compact” as possible while still spanning the space of interest.
Interpretation in Data Science and Machine Learning
Span and linear dependence are not just theoretical constructs; they guide how we think about data transformations and feature engineering. For example, if a set of features is linearly dependent, one of those features may not provide new information. Identifying such dependencies helps reduce dimensionality without losing meaningful representational power.
Understanding these concepts in higher-dimensional spaces also helps clarify how data can be represented, how to check for redundancy in feature sets, and how to efficiently project data onto lower-dimensional manifolds (such as in Principal Component Analysis or other dimensionality reduction techniques).
Potential Follow-Up Questions
How do we interpret span in higher dimensions?
In higher-dimensional spaces, the idea is essentially the same. The span of a set of vectors remains the set of all possible linear combinations. You can visualize it more abstractly as the subspace generated by those vectors. In three-dimensional space, for instance, the span of two non-collinear vectors is a plane. In general d-dimensional space, the span can be any k-dimensional subspace, depending on how many vectors you choose and whether they are linearly independent.
A key takeaway is that even if a space is high-dimensional, the span is still defined in exactly the same way, but we rely on abstract reasoning rather than direct visualization.
Why is linear independence important for basis vectors?
Linear independence is vital because a basis is defined as a linearly independent set of vectors that spans a space. If the vectors are not linearly independent, they cannot serve as a basis, since one basis vector could be expressed as a combination of the others, rendering it superfluous.
This has direct implications in machine learning when constructing sets of features or hidden layer representations. You want each feature (or each learned component) to capture new information. Redundant (linearly dependent) features can lead to computational inefficiency and sometimes numerical instability in methods like regression or gradient-based optimization.
Is it possible for a set of vectors to be linearly dependent yet still span a space?
Yes. A linearly dependent set might still span the same space as a smaller, linearly independent subset. Consider three vectors in R^2, where two of them are linearly independent, and the third is a linear combination of the other two. Those three vectors still span the same 2D plane, but they are collectively linearly dependent. The set can be reduced (by removing the redundant vector) to a smaller set that remains a spanning set but is now linearly independent.
This situation often arises when data scientists have more features than they need. The entire set can describe a subspace of interest, but some features may be redundant and removable without losing the ability to represent data in that subspace.
How do we detect linear dependence in practice?
One common approach is to form a matrix whose columns are the vectors in question. By performing row-reduction, computing the rank of that matrix, or checking its determinant in a square case, you can determine whether the columns are linearly dependent. If the rank is less than the number of columns, the column vectors are linearly dependent.
In computational terms, algorithms like singular value decomposition (SVD) can also reveal linear dependence by showing zero (or near-zero) singular values for the data matrix.
How do these concepts apply to deep learning architectures?
Neural network layers can produce representations of data that are sometimes close to being linearly dependent, especially if certain parameters converge to similar values. This can happen in practice when networks learn redundant features. Techniques such as weight regularization, batch normalization, and dropout are designed (among other reasons) to help avoid pathological convergence scenarios where neurons become highly correlated (and hence produce near-linearly dependent outputs), which can undermine generalization.
Understanding the geometry of feature embeddings is therefore crucial when designing models and diagnosing potential issues such as vanishing or exploding gradients, or overfitting. Linear dependence in intermediate representations might signal that the model has effectively fewer “degrees of freedom” than it appears to have on paper, which might limit performance on complex tasks.
These principles help guide effective architectures and training practices, ensuring that each part of the network contributes meaningfully to the overall learned representation.