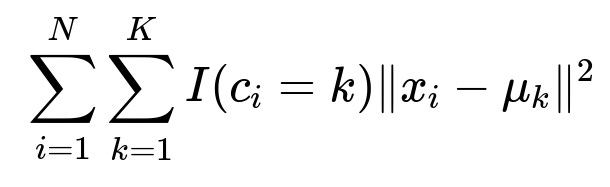ML Interview Q Series: Explain how Forgy Initialization, Random Partition Initialization, and the k-means++ Initialization strategy differ from one another.

📚 Browse the full ML Interview series here.

Comprehensive Explanation

K-means clustering is often expressed through the objective of minimizing the sum of squared distances between data points and their assigned cluster centers. The classical K-means cost function can be shown as

where N is the number of data points, K is the number of clusters, c_i is the assigned cluster index for data point x_i, and mu_k is the centroid of cluster k. The choice of initial centroids mu_k plays a major role in the speed of convergence and the quality of the final clustering result. Three well-known methods for initializing K-means are Forgy, Random Partition, and k-means++.

Forgy Initialization

In this method, the algorithm randomly picks K distinct points from the dataset to serve as initial centroids. It is straightforward to implement and widely used in many standard libraries.

Forgy tends to place initial centroids in “actual” positions from your dataset. This can sometimes lead to a better spread of initial clusters than naive approaches if your data is large and well-mixed. However, it can also result in poor initialization if, by chance, the chosen points are too close together, creating suboptimal initial partitions.

Random Partition Initialization

In this approach, every data point in the dataset is randomly assigned to one of the K clusters. Then, the initial centroid for each cluster is calculated by taking the mean of all points assigned to that cluster.

A benefit of random partitioning is that it is simple and can be implemented quickly: you assign each data point to a cluster index at random, and then compute the cluster means. However, it can produce highly imbalanced initial assignments, or occasionally cluster assignments that cause many centroids to overlap if the random seed is unfortunate. These issues can lead to slower convergence or poorer local minima.

k-means++ Initialization

k-means++ carefully selects initial centroids to spread them out in a data-driven way. It starts by picking one point from the dataset uniformly at random. Next, for each subsequent centroid, it chooses a new point from the dataset with probability proportional to its squared distance to the nearest chosen centroid. This process tries to place centroids far apart.

This more structured approach often improves convergence speed and reduces the likelihood of converging to a bad local optimum. Empirically, k-means++ is frequently used in practice because it tends to generate better cluster quality and is still relatively fast, even for moderate to large datasets.

k-means++ does add a slight overhead at the beginning because it calculates distances from already chosen centroids in each step. However, this overhead is usually negligible compared to the potential benefit of improved cluster initialization.

Follow-up Questions

How does each method affect convergence and final cluster quality?

Forgy can lead to either good or poor results depending on the random draw of actual data points. Sometimes it gets a near-optimal solution quickly if the random picks happen to be representative. Other times it chooses centroids that are too close together, leading to suboptimal local minima.

Random Partition can have even higher variance in cluster quality because the initial means might be highly skewed if a disproportionate number of points get assigned to certain clusters. This can result in multiple iterations just to “correct” poor initial allocations, although for large datasets, random partitioning may still balance out to a decent spread occasionally.

k-means++ usually provides a much more stable and robust starting point, leading to faster convergence. By preferentially choosing centroids that are far apart, the algorithm is more likely to discover a “good” partition of the dataset right from the beginning.

Why is k-means++ considered the “best practice” for many real-world K-means tasks?

k-means++ addresses one of the main pitfalls of naive initialization: the risk of choosing centroids that are too close together. Because it spreads out the initial centroids, it systematically lowers the risk of bad clustering solutions. While the overhead in the centroid initialization step might be slightly higher than a simple random pick, the overall performance gain in terms of time to converge and final quality is typically substantial.

Moreover, library implementations like scikit-learn’s KMeans often use k-means++ as default precisely because it tends to produce high-quality results with minimal manual tuning. In large-scale setups, this overhead can be optimized further by sampling fewer candidate points at each step, or by parallelizing the distance computations.

In practice, do these approaches always guarantee finding the global optimum?

No. K-means (with any initialization) is a heuristic that usually converges to local minima. None of these initialization methods can guarantee the global optimum in every situation. However, k-means++ reduces the chances of getting stuck in a poor local minimum and frequently provides superior solutions compared to random initialization.

If the dataset is especially high dimensional or has a tricky structure, you might run the entire K-means clustering multiple times with different initial seeds and pick the result with the best objective score. Using k-means++ in these multiple runs further boosts the likelihood of finding a better local minimum.

Can you show a Python code snippet demonstrating how to use these initializations?

Below is a short snippet using scikit-learn to demonstrate how you might specify initialization strategies. Note that scikit-learn already has built-in support for k-means++, so we can simply specify init="k-means++". For Forgy, one would manually choose random samples from the dataset as initial centers. For random partition initialization, you would randomly assign labels first and compute means, but this is not directly supported as a built-in option.

import numpy as np
from sklearn.cluster import KMeans

# Create synthetic data
np.random.seed(42)
X = np.random.rand(100, 2)

# k-means++ initialization
kmeans_pp = KMeans(n_clusters=3, init="k-means++", n_init=10)
kmeans_pp.fit(X)
print("k-means++ Centroids:\n", kmeans_pp.cluster_centers_)

# Forgy-like initialization: select random points as initial centroids
random_indices = np.random.choice(len(X), 3, replace=False)
forgy_init = X[random_indices]

kmeans_forgy = KMeans(n_clusters=3, init=forgy_init, n_init=1)
kmeans_forgy.fit(X)
print("Forgy Centroids:\n", kmeans_forgy.cluster_centers_)

# Random Partition approach (manual)
# 1) Assign each point to a random cluster
random_labels = np.random.randint(0, 3, len(X))
# 2) Compute initial centers from these random labels
random_partition_init = np.array([X[random_labels == i].mean(axis=0) for i in range(3)])

kmeans_rp = KMeans(n_clusters=3, init=random_partition_init, n_init=1)
kmeans_rp.fit(X)
print("Random Partition Centroids:\n", kmeans_rp.cluster_centers_)

In this code:

• k-means++ is used by simply setting init="k-means++".

• Forgy is illustrated by directly selecting n_clusters points from the dataset as the initial centroids.

• Random Partition is approximated by randomly assigning cluster labels and then computing the centroid for each label.

What are the key drawbacks or pitfalls with each initialization?

Forgy is straightforward but could be a gamble if the random picks are poorly representative. In small or noisy datasets, it might skip essential structures in the data.

Random Partition can lead to clusters that make little sense initially, especially if the random label assignment is unbalanced, causing slow convergence.

k-means++ typically solves many of those problems but has a slight upfront cost for distance-based sampling. Nonetheless, the consensus is that it is more reliable for most real-world scenarios and is thus widely adopted.

When is random partition or simple random centroid picking sometimes preferred over k-means++?

In some large-scale, real-time streaming scenarios or extremely high-dimensional spaces, it might be costly to perform distance checks for each data point while choosing initial centroids, especially if the data arrives rapidly. Simple random picks or random partition can be faster to implement on the fly. Additionally, if your data distribution is already well-mixed or if you plan to run K-means multiple times anyway, simpler methods might be acceptable.

However, in most practical batch analytics settings, k-means++ remains the go-to method for generating high-quality clusters with fewer restarts.

Could we blend different initialization strategies or refine them further?

In principle, yes. Some implementations combine distance-based sampling with domain heuristics (e.g., weighting certain features more heavily). Another approach is to initialize using one technique (like random partition) and then refine the centroids with a few k-means++ steps. Yet, these hybrid methods are less common because k-means++ alone is typically robust enough for a wide range of use cases.