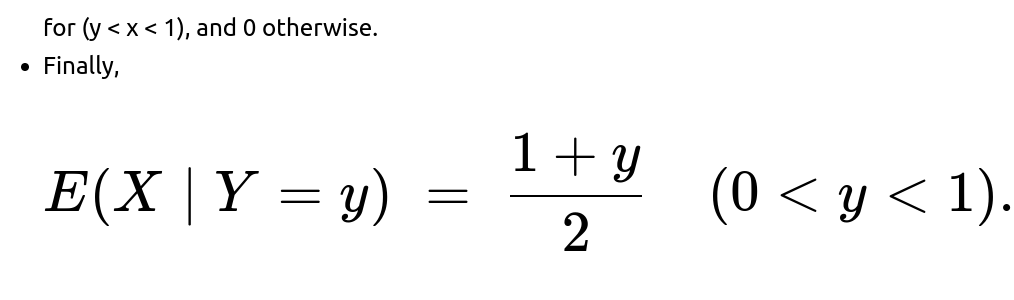ML Interview Q Series: Finding Conditional Density & Expectation via Joint/Marginal Density Calculations
Browse all the Probability Interview Questions here.
13E-4. The continuous random variables (X) and (Y) satisfy (f_{Y\mid X}(y \mid x) = \frac{1}{x}) for (0 < y < x), and the marginal density of (X) is (f_X(x) = 2,x) for (0 < x < 1), and zero otherwise. Find the conditional density (f_{X\mid Y}(x \mid y)) and also find (E(X \mid Y = y)).
Short Compact solution
From (f(x,y) = f_X(x),f_{Y\mid X}(y\mid x)), we obtain
(f(x,y) = 2) for (0 < x < 1) and (0 < y < x), and 0 otherwise.
The marginal density of (Y) is [ \huge \int_{x=y}^{1} 2 , dx ;=; 2 ,(1 - y)\quad\text{for }0 < y < 1. ]
Hence,
Comprehensive Explanation
Deriving the joint density
We are given:
(f_{Y\mid X}(y\mid x) = 1/x) for (0 < y < x).
(f_X(x) = 2,x) for (0 < x < 1).
The joint density (f(x,y)) of (X) and (Y) is (f_X(x),f_{Y\mid X}(y\mid x)). For the domain (0 < y < x < 1):
(f_{X}(x)) is (2x).
(f_{Y\mid X}(y\mid x)) is (1/x).
Thus for (0 < y < x < 1),
f(x,y) = (2x) * (1/x) = 2.
Outside this region, the density is 0 because either (x) is not in ((0,1)) or (y) is not in ((0,x)).
Finding the marginal density of (Y)
To get (f_Y(y)), we integrate out (x) from the joint density:
[
\huge f_Y(y) = \int_{x=y}^{1} f(x,y), dx = \int_{x=y}^{1} 2, dx = 2,(1 - y), \quad 0 < y < 1. ]
This step integrates from (x = y) to (x = 1) because for a given (y), (x) must be at least (y) (since (0<y<x)) and at most 1.
Determining the conditional density (f_{X \mid Y}(x \mid y))
By definition, ( f_{X \mid Y}(x \mid y) = \frac{f(x,y)}{f_Y(y)}. )
From above:
(f(x,y) = 2) for (y < x < 1).
(f_Y(y) = 2,(1 - y)) for (0 < y < 1).
Hence for (y < x < 1):
[
\huge f_{X \mid Y}(x \mid y) = \frac{2}{2,(1 - y)} = \frac{1}{,1-y,}. ]
Outside (y < x < 1), it is 0. This satisfies the standard properties of a density over (x\in(y,1)). It integrates to 1 over that interval, since (\int_{x=y}^{1} \frac{1}{1-y},dx = 1).
Computing the conditional expectation (E(X \mid Y = y))
The conditional expectation is:
[
\huge E(X \mid Y = y) = \int_{x=y}^{1} x , f_{X \mid Y}(x \mid y), dx = \int_{x=y}^{1} x ,\frac{1}{1-y}, dx. ]
We can evaluate that integral:
[
\huge \int_{x=y}^{1} \frac{x}{1-y}, dx = \frac{1}{1-y} \int_{x=y}^{1} x , dx = \frac{1}{1-y},\left[\frac{x^{2}}{2}\right]_{x=y}^{x=1} = \frac{1}{1-y} \left(\frac{1^2}{2} - \frac{y^2}{2}\right) = \frac{1 - y^2}{2(1-y)}. ]
Factor (1-y^2) into ((1-y)(1+y)). Then:
[
\huge \frac{(1-y)(1+y)}{2(1-y)} = \frac{1+y}{2}. ]
Thus for (0 < y < 1),
[
\huge E(X \mid Y = y) = \frac{1 + y}{2}. ]
Further Follow-Up Questions
Why do we integrate from x = y to x = 1 for fY(y)?
Because for any fixed (y\in(0,1)), the joint density is nonzero only if (y < x). Also, (X) itself is only supported on ((0,1)). Hence, for a given (y), the valid range of (x) is from (y) up to 1.
How does the domain affect real-world interpretation?
The condition (0 < y < x < 1) means that (Y) must be strictly less than (X), and both must lie between 0 and 1. This could represent many scenarios where one random variable is always constrained to be below the other, such as certain order statistics of uniform(0,1) random variables.
Could you verify that E(X|Y=y) is linear in y?
Yes. We found (E(X \mid Y = y) = (1 + y)/2). As a function of (y), that is a straight line: it passes through ((y, (1+y)/2)). So it is indeed a linear (affine) function in (y).
How to estimate or simulate these densities in practice?
If we wanted to empirically confirm these relationships from data:
We could generate samples ((X_i,Y_i)) by first drawing (X) from a Beta(2,1) distribution (since (f_X(x)=2x) on ((0,1)) is precisely Beta((\alpha=2,\beta=1))).
Then, for each sampled (X_i), draw a uniform random variable (U_i) on ((0,X_i)). That (U_i) would serve as (Y_i).
We could then verify that the empirical distribution matches the derived formulas, for instance by estimating (E(X \mid Y)) from the sample and checking it against ((1 + Y)/2).
Does the conditional density integrate to 1 over x in (y, 1)?
We can check:
[
\huge \int_{x=y}^{1} \frac{1}{,1-y,} , dx = \frac{1}{,1-y,} (1 - y) = 1. ]
So it’s a valid probability density function in (x) over the interval ((y,1)).
Edge cases when y approaches 0 or 1
If (y \to 0), then (f_{X\mid Y}(x \mid y)) remains (\frac{1}{1-0} = 1) from (x\in(0,1)). This matches the idea that if (Y) is near 0, (X) can be anywhere in ((0,1)) with uniform likelihood. Then (E(X \mid Y=0)=(1+0)/2=0.5).
If (y \to 1), (f_{X\mid Y}(x \mid y)) compresses to a small range between (x) just bigger than (y) and 1. Then (E(X \mid Y = 1)) would approach 1. Formally, for (y) very close to 1, (\frac{1+y}{2}) is close to 1.
These checks confirm the internal consistency of our solution.
Below are additional follow-up questions
How would you compute P(X > 0.5 | Y = y)?
One might want the conditional probability that (X) exceeds 0.5, given that (Y = y). From our conditional density of (X) given (Y=y), we know that (X) is restricted to lie between (y) and 1. Thus,
P(X > 0.5 | Y = y) =
0, if y >= 0.5 (because in that case the range of X starts from y, which is already >= 0.5, so X>0.5 is certain if y>=0.5).
The integral of f_{X|Y}(x|y) from x=0.5 to x=1 if y < 0.5 (since then the portion from 0.5 to 1 is valid in the range y < x < 1).
Using f_{X|Y}(x|y) = 1 / (1 - y) for y < x < 1, we break it down:
If y >= 0.5, then X>0.5 is guaranteed since X>y. So P(X>0.5 | Y=y) = 1.
If y < 0.5, then P(X>0.5 | Y=y) = integral from x=0.5 to 1 of [1/(1-y)] dx = [ (1)/(1-y) ] * (1 - 0.5 ) = (0.5)/(1-y).
Hence:
For 0 < y < 0.5, P(X>0.5 | Y=y) = 0.5 / (1 - y).
For 0.5 <= y < 1, P(X>0.5 | Y=y) = 1.
A subtlety here is that once y crosses 0.5, the event X>0.5 is no longer partial; it is certain that X>0.5 because X>y. A real-world pitfall might be forgetting that if y is already larger than 0.5, then X must be larger than y, and so obviously larger than 0.5.
Does the condition Y < X imply Y can never equal X, and how does that affect the densities?
Yes, from the setup 0 < y < x < 1, we see that Y strictly has to be less than X. Therefore, the probability that Y=X is zero. In continuous random variables, events like X=Y typically have probability 0 anyway, but here the support is explicitly restricted to strictly y < x. In real-world interpretations, we might say “Y is some random fraction of X that is guaranteed to be smaller.” A pitfall is incorrectly including the boundary y=x in an integral or forgetting that the range is strictly y<x. If one does so, the integrals or probabilities might be computed incorrectly, leading to slight domain mistakes in the calculations.
What if we need the variance Var(X | Y = y)?
We can compute the conditional variance of X given Y=y by using the formula Var(X | Y=y) = E(X^2 | Y=y) - [E(X | Y=y)]^2. We already know E(X|Y=y) = (1+y)/2. So we first need E(X^2 | Y=y). Using the conditional density f_{X|Y}(x|y) = 1/(1-y) for y < x < 1:
E(X^2 | Y=y) = integral from x=y to 1 of x^2 * [1/(1-y)] dx.
Compute that integral:
(1/(1-y)) * [ x^3/3 ] from x=y to x=1 = (1/(1-y)) * (1^3/3 - y^3/3) = (1/(3(1-y))) * (1 - y^3).
Factor 1 - y^3 = (1 - y)(1 + y + y^2). So we get
(1/(3(1-y))) * (1 - y)(1 + y + y^2) = (1/3) * (1 + y + y^2).
Hence:
E(X^2 | Y=y) = (1 + y + y^2)/3.
Then we already have E(X|Y=y) = (1 + y)/2. Its square is ((1+y)/2)^2 = (1 + 2y + y^2)/4. Thus
Var(X | Y=y) = E(X^2 | Y=y) - [E(X|Y=y)]^2 = ( (1 + y + y^2)/3 ) - ( (1 + 2y + y^2)/4 ).
We can compute that difference carefully:
Put both terms under a common denominator of 12: (4(1 + y + y^2))/12 - (3(1 + 2y + y^2))/12 = [4 + 4y + 4y^2 - (3 + 6y + 3y^2)] / 12 = (4 + 4y + 4y^2 - 3 - 6y - 3y^2)/12 = (1 - 2y + y^2)/12 = ( (1 - y)^2 ) / 12.
Thus
This is a crucial formula to know if you want to quantify how variable X can be around its conditional mean. A subtlety is to double check the arithmetic, because it’s easy to make slip-ups in integrating or simplifying polynomials. A real-world pitfall is ignoring how the range of X shrinks as Y gets larger, causing the variance to decrease as y grows. Indeed, if y is close to 1, then there is little room for X to vary above y, so the variance shrinks.
Is X independent of Y in this model?
No. If X and Y were independent, the joint density would factor into f_X(x)*f_Y(y) over the entire domain. However, we see that Y < X is a structural dependence: Y depends on X in that it cannot exceed X. Also, from the formula for f_{X|Y}(x|y) = 1/(1-y) for x>y, we see that knowledge of Y changes the distribution of X. If Y were near 1, X is forced to lie in a narrow region close to 1. That is not what would happen if X and Y were independent (in that scenario, X would not be restricted to be bigger than Y). A practical pitfall is to treat them as though they are independent and do a naive factorization f(x,y)=f_X(x)f_Y(y) for x,y in (0,1), which would be incorrect.
How would we handle transformations such as U = X - Y or V = Y / X?
A follow-up might be to investigate different transformations. For instance, we might define a new variable U = X - Y. Because we know 0 < y < x < 1, it follows 0 < U < 1 - y. Another interesting choice is V = Y/X. If Y is uniform on (0, X), V should be uniform on (0, 1). Indeed, if Y | X=x ~ Uniform(0, x), then V = Y/x ~ Uniform(0, 1).
If we wanted to find the joint distribution of (X, V), we would use standard transformations of random variables. A subtle point is to keep the correct support. V only goes from 0 to 1, while X goes from 0 to 1. The pair’s distribution would reflect that Y = X * V. One might incorrectly assume V is independent of X, but in fact from the generation perspective, Y is uniform on (0,X). So once X is chosen, V is uniform(0,1). That does indeed make V independent of X. Hence V is uniform(0,1) overall, and X still has the Beta(2,1) distribution. The pitfall is incorrectly mixing up the support constraints if you pick transformations incorrectly (e.g., mixing up Y with V incorrectly in integration bounds).
Could boundary conditions at Y=0 or Y=1 cause issues in some physical applications?
Yes. Although mathematically we say 0 < y < x < 1, in real measurement scenarios, one might measure Y=0 or Y=1 exactly due to rounding or sensor constraints. The formal model states these are events of measure zero, but in practice you could get a corner case if Y is effectively measured as 0 or 1. The main pitfall is how to interpret or handle real data that might be slightly outside the strict domain or exactly on the boundary. Often, one might treat Y=0 as being a near-zero measurement and proceed with the limiting distribution. But you have to be careful in real data to ensure that the theoretical model is consistent with the possibility that Y might be extremely close to or at 1. If Y=1 in data, then X must be at least 1, but the model says X < 1 always, so that would highlight a mismatch between model and reality.
How might numerical integration or sampling fail near the boundary?
If you attempt to estimate integrals numerically, you must handle the region y < x < 1 carefully. For instance, if you do a 2D grid over x,y in [0,1], you have to respect the domain where x>y, not the entire square [0,1]x[0,1]. Failure to do so might cause you to average or integrate over an incorrect region, artificially introducing biases. Another pitfall is if you implement a Monte Carlo sampler incorrectly and don’t enforce x>y, you could end up with meaningless results.
When dealing with real data, how would you test the assumption that Y is uniform from 0 to X?
To verify that the conditional distribution of Y given X is truly uniform on (0, X), you could fix a subset of observations where X is approximately some value x_0, then check the empirical distribution of Y in [0, x_0]. If it is indeed uniform, the empirical CDF of Y/x_0 would be close to the standard Uniform(0,1) diagonal line. A subtlety is ensuring that X is truly varying according to f_X(x)=2x on (0,1), i.e., you might also check the distribution of X in the data. A real-life pitfall is that data might not reflect these perfect theoretical forms, so you often need goodness-of-fit tests or other robust checks.
How might the correlation between X and Y behave as y changes?
Intuitively, if Y is forced to be less than X, we expect a positive relationship. For instance, larger X allows Y to be larger as well. This correlation can be computed directly from the joint density, but we already see from the strict ordering that Y is “trailing behind” X. A pitfall is to assume linear correlation is close to 1 or 0, but the correlation is actually some fraction that might be moderate. In fact, if we tried to compute Corr(X, Y) from first principles:
We know Y cannot exceed X, so a strong monotonic relationship is implied.
However, it is not a perfect correlation because Y is also uniformly distributed below X for each X.
Hence, the correlation is strictly positive, but it’s not 1. Determining that exact correlation or rank correlation involves working through integrals with f(x, y) = 2 for 0 < y < x < 1. Doing it incorrectly (for example ignoring the domain constraints) is a potential pitfall.