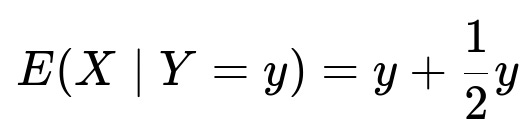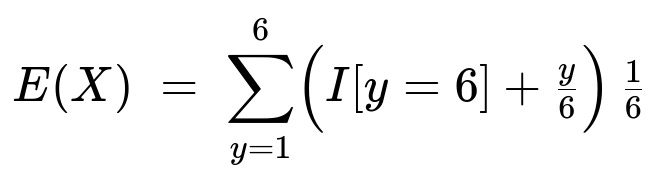ML Interview Q Series: Finding Expected Values in Staged Random Trials Using Conditional Expectations
Browse all the Probability Interview Questions here.
13E-8. You first toss a fair coin five times. Next, you toss the coin as many times as the number of heads showing up in these five tosses. Let the random variable X be the number of heads in all tosses of the coin, including the first five tosses. Use conditional expectations to find E(X). Then, you first roll a fair die once. Next, you roll the die as many times as the outcome of this first roll. Let the random variable X be the total number of sixes in all the rolls of the die, including the first roll. Use conditional expectations to find E(X).
Short Compact solution
For the coin-toss scenario, let Y be the number of heads in the first five tosses. The expected value of X given Y=y is y + (1/2)*y because the first five tosses contribute y heads, and the next y tosses contribute on average (1/2)*y heads. By the law of total expectation:
E(X) = E(Y) + (1/2)*E(Y) = (3/2)*E(Y).
Since E(Y) = 5/2 (because in 5 fair tosses, the expected number of heads is 5 * 1/2 = 5/2), we get
E(X) = (3/2) * (5/2) = 15/4 = 3.75.
For the die-roll scenario, let Y be the outcome of the first die roll. The probability of rolling any face is 1/6. The expected value of X given Y=y is an indicator contribution if y=6 (which gives exactly one six for the first roll) plus the expected number of sixes from the additional y rolls (which is y/6). Hence:
E(X | Y=y) = I[y=6] + (y/6),
and using the law of total expectation over y=1..6 with probability 1/6 each:
E(X) = (1/6)* [ (I[1=6] + 1/6) + (I[2=6] + 2/6) + ... + (I[5=6] + 5/6) + (I[6=6] + 6/6 ) ].
Evaluating this sum gives 0.75.
Comprehensive Explanation
Part A: Coin-toss scenario
Random variable definitions
We first toss a fair coin 5 times. Let Y be the number of heads observed in these first 5 tosses.
We then toss the coin Y additional times.
Let X be the total number of heads across all tosses (the initial five tosses plus the extra Y tosses).
Breaking down E(X | Y) When Y=y, we already know there are y heads in the first five tosses. We then perform y additional coin tosses; each new toss has probability 1/2 of being a head, so the expected number of heads in those y extra tosses is (1/2)*y. Therefore:
Inside the right-hand side:
y is the number of heads in the first 5 tosses.
(1/2)*y is the expected number of heads in the subsequent y tosses.
Law of total expectation The law of total expectation states in plain text that E(X) = E[ E(X | Y) ]. Substituting our expression for E(X | Y):
We must now find E(Y). Since Y is the number of heads in 5 independent fair coin tosses, Y follows a Binomial(5, 1/2) distribution, and its mean is 5*(1/2) = 5/2. Hence:
Part B: Die-roll scenario
Random variable definitions
We first roll a fair six-sided die one time. Let Y be the value we see on that first roll.
We then roll the die Y more times.
Let X be the total number of sixes across all rolls (the initial single roll plus the subsequent Y rolls).
Breaking down E(X | Y) When Y=y, there are two contributions to X:
The first roll is a six with probability 1/6. So if y=6, that guarantees exactly one six from that first roll. If y is not 6, the contribution from the first roll is 0 sixes.
The subsequent y rolls contribute on average y/6 sixes, because each roll independently has a 1/6 chance to show a six.
Thus we can express:
In that expression:
I[y=6] is an indicator that equals 1 if y=6, and 0 otherwise.
y/6 is the expected number of sixes from the additional y rolls.
Law of total expectation Again, using E(X) = E[ E(X | Y) ], and the fact that each outcome y in {1,2,3,4,5,6} occurs with probability 1/6, we get:
Evaluating the indicator part: I[1=6], I[2=6], ..., I[5=6] are all 0, while I[6=6] = 1. Summing these terms leads to:
E(X) = (1/6) * [(0 + 1/6) + (0 + 2/6) + (0 + 3/6) + (0 + 4/6) + (0 + 5/6) + (1 + 6/6)] = (1/6) * [ (1/6 + 2/6 + 3/6 + 4/6 + 5/6) + (1 + 6/6) ] = (1/6) * [ 15/6 + (1 + 1) ] = (1/6) * [ 15/6 + 2 ] = (1/6) * [ 15/6 + 12/6 ] = (1/6) * (27/6) = 27/36 = 3/4 = 0.75.
Hence the total number of sixes we expect to see in this random process is 0.75.
Follow-up Question: Why does conditional expectation help here?
Conditional expectation is often the most direct way to handle scenarios where the total number of trials depends on some random quantity. By conditioning on Y (the random number of additional trials), we can treat Y as “fixed” within that conditional space, compute an expected value that is simpler, and then average (take expectation) over all possible values of Y. This avoids more complicated summations and leverages the law of total expectation to decouple the randomness of how many extra trials are performed from the randomness of successes within those trials.
Follow-up Question: How would these results change if the coin or the die were not fair?
If the coin were biased with probability p of landing heads, then each additional toss would contribute on average p heads. In the coin example:
E(X | Y = y) would be y + p*y, and if Y is Binomial(5, p), then E(Y) = 5p. You would still use E(X) = E[ E(X | Y) ] = E(Y) + p E(Y) = (1 + p)*E(Y). Thus:
E(X) = (1 + p) * 5p.
For the die scenario, suppose each face of the die had a probability distribution that might differ from 1/6. Then the chance of rolling a six, call it q, would change the expected number of sixes in Y additional rolls to q*Y. Also, the first roll itself is a six with probability q, so:
E(X | Y = y) = I[y=6 in the first roll’s distribution] + q*y,
where I[y=6 in the first roll’s distribution] equals 1 if that face in the first roll is “six” (though if the probabilities are not uniform, we must carefully consider the distribution of that first outcome). The law of total expectation again sums over all possible faces y with their probabilities.
Follow-up Question: Could we solve these problems without conditional expectation?
In principle, you can count the total number of heads (or sixes) by building a more complicated sum of probabilities. For example, with the coin, you would sum over the joint distribution: Probability(Y = y) times the probability of getting a certain number of heads among those y additional tosses. While it is doable, it becomes combinatorially more complex. Conditional expectation neatly short-circuits this combinatorial explosion, since E(X) = E( E(X | Y) ) is typically the most concise and elegant approach.
Follow-up Question: How do we simulate these scenarios in Python?
Below is a simple Python code snippet illustrating Monte Carlo simulation for the coin-toss problem. We can similarly adapt it for the die scenario.
import random
import statistics
def simulate_coin_scenario(num_trials=10_000_00):
results = []
for _ in range(num_trials):
# First 5 tosses
first_tosses = [random.choice([0,1]) for _ in range(5)] # 0 for tails, 1 for heads
y = sum(first_tosses)
# Next y tosses
next_tosses = [random.choice([0,1]) for _ in range(y)]
# Total heads
total_heads = sum(first_tosses) + sum(next_tosses)
results.append(total_heads)
return statistics.mean(results)
print(simulate_coin_scenario())
By running a large number of trials, we would see the simulated mean approach 3.75 for the coin scenario.
Similar simulation for the die scenario would replace the coin toss logic with random.randint(1,6) and check if it equals 6, then proceed with the Y additional rolls. We would see the mean of X approach 0.75 in that case.
Below are additional follow-up questions
What if we need to compute Var(X) instead of E(X)?
To find the variance of X, we can still leverage conditional expectations but extend our approach to use the law of total variance:
In words, we split the overall variance into the “expected conditional variance” plus the “variance of the conditional mean.” We already know how to compute E(X | Y). Hence:
Compute Var(X | Y = y). For the coin scenario, if Y = y, then X = y + Z, where Z is the number of heads in y new tosses. Z follows a Binomial(y, 1/2) if the coin is fair. Then Var(Z) = y*(1/2)*(1/2) = y/4. Hence Var(X | Y=y) = Var(y + Z) = Var(Z) = y/4.
Take the expectation of that expression: E[Var(X | Y)] = E(Y/4) = (1/4)*E(Y). For Y ~ Binomial(5, 1/2), E(Y) = 5/2, so this part is (1/4)*5/2 = 5/8.
Then compute Var(E(X | Y)) = Var( y + (1/2)*y ) in the coin scenario. Since E(X | Y = y) = (3/2)y, we need Var((3/2)y) = (9/4)Var(y). For Y ~ Binomial(5, 1/2), Var(Y) = 5(1/2)(1/2) = 5/4. So this becomes (9/4)(5/4) = 45/16.
Sum them: 5/8 + 45/16 = 5/8 + 45/16 = 10/16 + 45/16 = 55/16 = 3.4375.
That gives Var(X) for the coin scenario. A similar process applies to the die scenario, with Y ~ Uniform{1..6}, E(X | Y) = I[Y=6] + Y/6, and so on. In an interview, explaining every detail of this breakdown shows your mastery of random variable decomposition and the importance of the law of total variance.
A potential pitfall is forgetting that Var(X | Y) is not simply Var(Z) unless you carefully account for the heads already counted in the first stage. Another pitfall is neglecting the correlation induced by the fact that Y determines both how many extra tosses you do and how many heads or sixes you might accumulate in total.
What if we want the entire probability distribution of X, not just its expectation?
When we move beyond the mean to the actual distribution (for instance, the probability that X = k for k=0,1,2,...), conditional expectations alone are not enough. We can proceed by conditioning on Y and then convolving the distributions. For the coin case:
Y ~ Binomial(5, 1/2).
Condition on Y=y, then X = y + (the number of heads in y new tosses).
The number of heads in y new tosses is Binomial(y, 1/2).
Hence the distribution for X given Y=y is a shift of a Binomial(y, 1/2) by y (because we already have y heads from the first five). To combine them, we sum over y from 0..5:
P(X = k) = Sum over y of [ P(Y=y) * P( y + (Binomial(y, 1/2)) = k ) ].
A subtlety arises because if y = k, that implies the binomial term from the additional y tosses must be 0, or if y = k-1, then the binomial term must be 1, and so on. This can be done systematically, but it gets more complicated than just computing E(X). In an interview, you might highlight that this is generally feasible but more involved.
A potential pitfall is that people sometimes incorrectly assume the distribution of X is just a single binomial or a single known distribution. In reality, it is a mixture of binomials weighted by the distribution of Y.
How would we handle a scenario where Y depends on something other than just the number of heads or the actual value of the die—like Y is some function g of the first outcomes?
If instead of rolling the die or tossing the coin a number of times equal to the exact outcome of the first stage, we do a function g(Y) extra trials, the law of total expectation still holds:
E(X) = E( E(X | Y) ).
But now, if Y = y, we do g(y) more coin tosses or die rolls. We would adjust the conditional expectation to:
E(X | Y = y) = (heads or sixes in the first stage) + (expected heads or sixes in g(y) new trials).
For the coin: E(X | Y=y) = y + p*g(y) if the coin has probability p of heads. Or for the die: E(X | Y=y) = (1 if y=6 else 0) + (g(y)/6). The rest is straightforward so long as you keep track of the function g.
A subtle real-world pitfall is ensuring that g(Y) is well-defined. For instance, if g(Y)=0 for some Y, that means no additional trials occur in that scenario; also if g(Y) can be negative or a real value, it no longer fits a typical “number of additional trials.” In an interview, demonstrating that you understand domain constraints is crucial.
What if the coin or die outcomes become correlated across trials?
All the calculations above assume independence across different tosses or rolls. If the outcomes become correlated—say we have a die that “learns” or changes bias after each roll—then we can’t simply multiply the probability p by the number of trials to get the expected count of “successes.” We must explicitly account for how each new trial’s probability or distribution depends on previous outcomes.
In such a correlated environment, even the law of total expectation can still hold, but E(X | Y) might be more complicated to derive if the probability of success in the new trials depends on Y not just as “how many times” but also as an input to the success probability. A big interview mistake is to assume unconditional independence of trials when the problem statement might have subtle correlation.
What if we introduce a stopping rule, for example, that we stop tossing coins or rolling dice if we see a certain number of heads or sixes?
Stopping rules can fundamentally change the distribution of Y or how many total tosses/rolls happen. The law of total expectation can still be applied, but we have a new definition for Y. For instance, if we keep tossing the coin until we see 2 heads, then Y would be the total toss count needed to achieve that condition. Y might follow a Negative Binomial distribution. If after observing the random Y, we do even more steps, the approach is still:
E(X) = E( E(X | Y) ).
But now E(X | Y = y) must handle the events leading up to y tosses with that stopping rule in place. Real-world pitfalls include ignoring boundary conditions (e.g., what if you never see 2 heads?), or incorrectly mixing up geometric vs. negative binomial distributions.
How do we approach a scenario where partial information about Y is revealed?
Sometimes in real-life experiments, you don’t see the final Y but only partial outcomes. You might ask: “Given partial knowledge about how many heads we’ve seen so far, can we update the expected total number of heads?” This is essentially a Bayesian updating or an online conditional expectation approach. You look at the partial data, infer the distribution of Y (and future tosses), then recalculate E(X) given the partial information.
A subtlety here is that Y (the total from the first stage) might still be partially observed, so one must treat Y as a random variable with a partially updated distribution (posterior). This is more advanced, but it impresses interviewers if you can demonstrate that partial reveals can be integrated using the same “condition on what you know” principle.
Are there real-world constraints that invalidate the assumption of a fixed probability p (for coins) or 1/6 (for each face of a die)?
Yes. Physical coins might be slightly unbalanced due to wear or production flaws. Dice might be misaligned or have faces with different mass distribution. If the probability p changes from toss to toss or is never truly known, we might need to estimate it. One approach is to treat p as another random variable with some prior distribution, leading to a Bayesian analysis. We would then replace the fixed expectation p with its expected value given the prior and the data observed.
A pitfall is that ignoring these physical imperfections can yield biased estimates, especially if the number of additional trials is large. For instance, if the coin is heavily biased but you assume a fair coin, you’ll miscalculate E(X). Interviewers might want to see how you’d handle or check for bias in a real experiment.
What happens if Y could be zero, leading to no additional trials?
In the coin scenario, it’s clearly possible that Y=0 if all five initial tosses are tails. That means zero additional tosses. The law of total expectation trivially accommodates that case: E(X | Y=0) is 0 heads from the extra stage plus whatever heads you already had from the first stage (which in that scenario is 0). So E(X | Y=0) = 0. This is straightforward, but a common pitfall is to forget that with Y=0, no more heads can be added, so the total is just the heads from the initial stage.
In the die scenario, Y can’t be zero if we’re talking about a standard 6-sided die with faces 1..6. However, a custom die with a face labeled “0” or any alternative distribution can lead to a scenario where you might not roll anymore. Handling Y=0 is consistent with the same formula E(X | Y=0) = “heads or sixes from the first stage” plus 0 from additional trials.
What if we want to generalize to multiple stages?
We can imagine a chain of events: (1) toss the coin 5 times, get Y heads. (2) toss the coin Y times, get Z heads. (3) toss the coin Z times, get W heads, and so on. We could define X = total heads across all these stages. We still can apply conditioning iteratively—first condition on Y, then within that condition on Z, etc. The expectation would be computed by nested applications of E(X) = E( E(X | Y) ) and so forth. This quickly becomes a branching or multi-stage Markov process where each stage depends on the result of the previous stage.
A subtle pitfall is that infinite sequences can arise if you never end up with zero additional tosses. One must ensure that the random process terminates or that you can define the total count in the limit. Demonstrating knowledge of such complexities is a strong way to highlight that you understand advanced random process modeling.