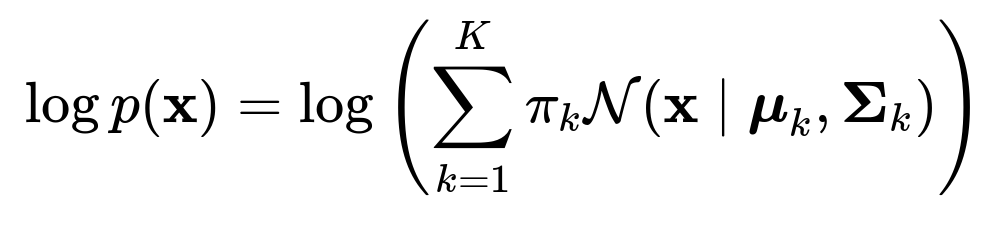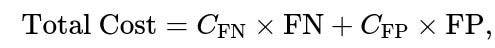ML Interview Q Series: Fraudulent Transaction Anomaly Detection with Gaussian Mixture Models.

📚 Browse the full ML Interview series here.

Say we are using a Gaussian Mixture Model (GMM) for anomaly detection on fraudulent transactions to classify incoming transactions into K classes. Describe the model setup formulaically, how to evaluate the posterior probabilities and log likelihood, and how to determine if a new transaction should be deemed fraudulent.

A useful way to think about a Gaussian Mixture Model (GMM) in this scenario is that we are modeling the distribution of legitimate transaction behaviors (and potentially multiple types of fraudulent behaviors if we wish). Each component in the mixture model captures one “cluster” or “type” of transaction. After fitting this model, we can then measure how likely it is that a new transaction belongs to any of these clusters. If the likelihood is sufficiently low, we flag the transaction as anomalous or fraudulent.

Model Setup

In a GMM, each data point (transaction) is assumed to be generated by one of K underlying Gaussian distributions. Each Gaussian distribution has a mean vector and covariance matrix, and we also have mixing coefficients that describe how prevalent each distribution is in the data. We write the mixture model for a d-dimensional transaction vector x as:

The GMM parameters are typically obtained via the Expectation-Maximization (EM) algorithm, but conceptually, we can treat them as already fit once we have trained on a labeled or unlabeled (in the sense of no cluster labels, just normal data) dataset that is representative of typical transactions.

Evaluating Posterior Probabilities

In practice, this quantity tells you how likely it is that the transaction came from component k’s Gaussian distribution, relative to the other Gaussian components in the mixture.

Log Likelihood

The log likelihood for a single transaction x under the entire mixture model is the natural log of p(x). In other words:

Determining if a New Transaction is Fraudulent

Anomaly or fraud detection typically involves scoring how “typical” or “atypical” a new transaction is under the learned distribution. A common approach is to compute the likelihood of the new transaction under the mixture model and compare it to a threshold. One practical approach is:

Because GMMs can capture multiple “modes” of normal behavior, the threshold can come from analyzing the empirical distribution of log-likelihood values for the training set (possibly cross-validation or some held-out set). You might, for example, set the threshold so that 99.9% of the legitimate transactions in your training data have a likelihood above it, and any transaction that falls below that threshold is flagged as anomalous.

This method depends greatly on the assumption that your training set accurately represents the normal distribution of transactions (and possibly well-known fraudulent transactions if included in the model). If certain forms of fraud are missing from training, the model may not be well-calibrated for those.

Below is a short Python snippet showing an example approach using scikit-learn’s GaussianMixture for anomaly detection. The code is illustrative for how one might train the model and then compute log probability scores for classification:

from sklearn.mixture import GaussianMixture
import numpy as np

# Suppose X_train is your training set of transactions (N x d array)
# and you pick K for the number of mixture components
K = 5
gmm = GaussianMixture(n_components=K, covariance_type='full', random_state=42)
gmm.fit(X_train)

# For a new transaction x_new (1 x d array), compute the log-likelihood:
log_prob = gmm.score_samples(x_new.reshape(1, -1))  # shape must be (1, d)

# Compare log_prob to a threshold (say threshold = -20.0):
threshold = -20.0
if log_prob < threshold:
    print("Flag as fraudulent")
else:
    print("Likely normal")

The core idea is that the GMM gives you a density estimate for what “typical” data looks like. If your new data point has a very low density, it suggests it is atypical, which in the fraud detection domain translates to potential fraud.

What if the Transaction Data is Very High Dimensional?

When transaction features are numerous or heavily correlated, GMMs can struggle with parameter estimation if we attempt to fit a full covariance matrix for each component. Covariance matrices in high dimensions may lead to overfitting, require large amounts of data, and be expensive to estimate. One practical solution is to restrict the covariance matrices (e.g., using “diagonal” or “spherical” covariance types). Another approach is to first perform dimensionality reduction (like PCA) and then fit a GMM on the lower-dimensional subspace.

How do we Choose K?

Choosing the number of components K can be done by methods like the Bayesian Information Criterion (BIC) or the Akaike Information Criterion (AIC). You fit multiple GMMs with different K values and pick the one that optimizes your criterion of choice. Too many components might overfit, while too few might underfit the data distribution. You could also consider domain-specific knowledge about how many transaction “clusters” you expect or standard cross-validation approaches.

What if the Frauds are not Gaussian-like?

One important subtlety arises if the fraudulent transactions do not necessarily follow something that is well-approximated by a Gaussian distribution. If the fraud distribution is sufficiently different from your normal data distribution, this might still be fine, because GMM-based anomaly detection primarily relies on spotting transactions that have low likelihood under the learned “normal” distribution. However, if you are also modeling multiple known fraud modes as separate Gaussians, you should ensure that the data for those fraud modes in training is representative enough. In scenarios where fraudulent behavior changes drastically or is adversarial, GMMs alone can become less effective, and you may have to incorporate more sophisticated or adaptive approaches.

Follow-Up Question: Can we Apply the GMM Approach if we Only Have Labels for Legitimate Transactions and No Labels for Fraud?

Yes, you can treat your data under the assumption that most of it is legitimate and learn the GMM as an unsupervised density estimation approach that captures the main modes of genuine transaction behaviors. Because you lack fraudulent labels, the model will not explicitly learn how to represent fraud, but it will learn the distribution of normal behavior. You can then flag transactions whose likelihood is below a threshold. That threshold can be chosen such that it balances the false-positive rate (too many normal transactions flagged) and the false-negative rate (fraudulent transactions that are missed). Sometimes domain experts or cost-based metrics (e.g., the cost of a missed fraud vs. the cost of investigating a flagged transaction) guide where to set that threshold.

One additional detail is that in purely unsupervised anomaly detection, GMM might sometimes allocate components to outliers and effectively “explain them away,” thus decreasing the difference between normal and anomalous points. To mitigate that, you might consider robust mixture modeling techniques or put constraints on the mixture components (like ignoring those that have very small mixing weight or restricting how small the covariance can become).

Follow-Up Question: How Can We Improve Robustness if the Covariance Estimation is Unstable?

One option is to constrain the covariance type in the GMM to be “diag” (diagonal) instead of “full.” A diagonal covariance matrix drastically reduces the number of parameters and might be more robust in higher-dimensional settings with limited data. Another approach is to add regularization to the covariance estimation, sometimes called a regularization term or prior on the covariance matrices. In scikit-learn’s GaussianMixture, there is a parameter called “reg_covar” that enforces a minimum variance. This ensures none of the covariance matrices can collapse too aggressively and become singular or ill-conditioned.

Another practical safeguard is to ensure you have a sufficiently large training dataset. If your data is extremely high dimensional and you have limited samples, you may want to perform some dimensionality reduction technique (PCA or autoencoders) before fitting a GMM. Additionally, you can combine GMM-based anomaly scores with other domain knowledge or with a supervised classifier if you have any labeled fraud examples.

Follow-Up Question: How Do We Handle Concept Drift if Fraudulent Patterns Evolve Over Time?

Concept drift is especially relevant in fraud detection, because fraudsters adapt. A static GMM that is trained once might fail to detect new types of anomalies that weren’t present in the training data. You might schedule periodic retraining of the GMM on newer data (only those transactions believed to be legitimate or previously verified). Alternatively, you could use an online or incremental learning approach, where the GMM parameters are updated continuously as new data streams in, discarding old data gradually. You could also maintain a “sliding window” of data or a buffer that captures recent normal behavior and re-estimate the model on that window to track changes. Of course, any new fraud that emerges is still not modeled unless it either appears in enough quantity or is flagged and labeled so that the system can explicitly learn it.

Follow-Up Question: What are Some Practical Considerations for Implementing Threshold-Based Detection?

In a real deployment setting, simply picking a threshold might cause practical issues if it is not carefully tuned. You might choose a threshold so that on historical labeled data (if available), you get an acceptable balance between:

False positives: Legitimate transactions flagged as fraud. False negatives: Fraudulent transactions that pass as legitimate.

One might also use the ROC curve (Receiver Operating Characteristic) or the Precision-Recall curve if you have some labeled data. You can pick a log-likelihood threshold that yields a suitable operating point. After picking the threshold, always keep an eye on changing transaction patterns. If your model is triggering too many false positives, your threshold might be too strict. If the model is missing obvious fraud patterns, your threshold might be too lenient or the model might need retraining.

Another detail is that not all fraud has the same cost. Certain large, suspicious transactions might warrant a different threshold from small transactions. You could condition on a high-level feature (transaction size) and vary the threshold accordingly. Alternatively, you might incorporate features that have domain-specific weighting. In any case, the threshold-based logic is typically straightforward to implement, but it can be tricky to tune in practice.

Follow-Up Question: Could We Combine GMM with Other Techniques for Better Fraud Detection?

Many practical fraud detection systems are ensemble-based. You might have a GMM-based unsupervised anomaly detector combined with a supervised classifier (e.g., XGBoost or a neural network) trained on known fraud examples. The GMM could provide an “anomaly score,” which is then another input feature to a downstream supervised model. This often improves performance, because the supervised model can learn from labeled data while still leveraging an unsupervised notion of “typicality.” You might also add rules or heuristics. For instance, if a transaction triggers certain domain-specific rules, it is flagged regardless of its GMM likelihood.

In some real-world systems, data is extremely dynamic and high volume, so you would also pay attention to computational efficiency. Training a GMM with a large K or in high dimensions can be computationally heavy. Approximate methods, streaming variants, or simpler distributions might be more scalable.

One approach is to see if a new transaction fits best into any single component in a reasonable way. If no single component gives a high posterior probability, this suggests the transaction is an outlier. Some systems might flag a transaction if the maximum posterior probability over all components is below a threshold. Another way is to rely on the overall mixture likelihood rather than just the maximum posterior. In some cases, analyzing the distribution of posterior probabilities can help identify suspicious transactions that do not align well with any known mixture cluster.

Follow-Up Question: Show a Short Theoretical Walkthrough of the EM Steps for GMM in Fraud Detection?

Even though in many real-world situations we rely on library implementations, it is beneficial in an interview to show you understand the EM logic:

Repeat until convergence of the log likelihood (or until changes in parameters become very small). This yields a fit mixture model capturing the distribution of your data. For fraud detection, we might have more normal transactions than fraudulent ones in the training data, so effectively the GMM learns a representation of “normal” with possibly a smaller cluster capturing some known fraud patterns if labeled or included in the same dataset.

Follow-Up Question: How Do We Adapt the GMM if We Actually Have a Small Number of Labeled Frauds?

Sometimes you have at least a limited amount of labeled fraud. One approach is to incorporate a semi-supervised strategy, such as training a GMM only on “normal” data for certain components, then explicitly adding one or more “fraud components” if there is enough fraudulent data to learn a distinct cluster. Another approach is to treat the small labeled fraud set as a separate class and train a mixture model that includes the normal cluster(s) plus an additional component for fraud. If the data for fraud is insufficient or too diverse, you risk overfitting. You can also do a weighted training procedure where “normal” data has one set of mixture components and the known “fraud” points are forced into their own cluster with a prior that encourages the separation. However, many real-world pipelines simply incorporate supervised classifiers for that portion, or treat fraud as out-of-distribution entirely.

Follow-Up Question: Are GMMs the Only Density Estimation Approach for Anomaly Detection?

Not at all. Alternative density estimation approaches could be Kernel Density Estimation (KDE), normalizing flows, autoencoder-based reconstructions, or one-class SVM. GMMs are often convenient and interpretable, but in very high-dimensional spaces, deep learning methods like variational autoencoders (VAEs) might learn more flexible representations of “normal” transaction patterns. However, GMM remains a solid baseline for a wide range of anomaly detection tasks. It is also relatively easy to interpret which mixture component a transaction belongs to.

Follow-Up Question: Could We Use Mahalanobis Distance from the Closest GMM Component?

Follow-Up Question: How Could We Evaluate This on a Historical Dataset of Transactions?

If you have historical transactions labeled as legitimate or fraudulent, you can:

Split the data into training and validation sets. Fit the GMM on the training set (primarily or exclusively legitimate transactions). Obtain the likelihood (or log-likelihood) scores on the validation set. For each point, you know if it is fraudulent or not. Compute metrics such as the True Positive Rate (TPR), False Positive Rate (FPR), or the Precision-Recall for various thresholds on the GMM likelihood. Choose the threshold that best matches your business or operational constraints (for example, you might want to minimize the cost of investigating flagged transactions vs. the potential loss from missed fraud).

You can continue refining the GMM (e.g., changing K, covariance constraints) or the threshold until you achieve a suitable balance of TPR and FPR. Alternatively, you might incorporate domain-specific features or transformations prior to the GMM to improve detection performance.

Follow-Up Question: What if the Fraudulent Distribution is Multi-Modal?

If you have a variety of different fraudulent patterns, you could either rely on the GMM’s ability to create multiple modes for normal vs. various fraud modes, or you could have a separate multi-component mixture specifically for fraud. But you typically need enough representative fraudulent data for each type of fraud in order to learn distinct Gaussian components for them. If you do not have enough samples for each type of fraud, the GMM might merge them into fewer modes or treat them as outliers. Real-world fraud detection is often challenging because fraud evolves quickly, and data for each new fraud type is initially scarce.

In conclusion (within the scope of a GMM-based framework), the usual practice is to fit a GMM to normal transaction data and use a low likelihood threshold for anomaly detection. If you have partial fraud data, you can try to incorporate it in separate mixture components or through other semi-supervised strategies. The log-likelihood of a new transaction under the fitted mixture model is the main scoring function. A very low log-likelihood is your indicator for something suspicious and potentially fraudulent.

---

Below are additional follow-up questions

What if the normal transaction distribution changes abruptly and we cannot periodically retrain the GMM right away?

Sudden shifts in normal behavior can occur in fraud detection. For example, during major shopping holidays or unexpected market events, normal transaction patterns might differ drastically from those observed during training. In such scenarios, a GMM trained on older data could flag a large portion of legitimate transactions as fraudulent because they deviate from the historical mean and covariance structures. This can spike false positives and overwhelm fraud investigation teams.

A deeper look:

• Adaptation Lag: If you cannot update your GMM parameters on new data quickly, the model may remain calibrated only to the old distribution. Consequently, a huge fraction of newly incoming transactions might appear as low-likelihood outliers.

• Temporary vs. Permanent Change: One subtlety is whether the shift in transaction behavior is temporary (e.g., a holiday week) or permanent (e.g., a new consumer behavior pattern triggered by some policy change). If it is a short-term pattern, you might need a short-term GMM that accounts for seasonal or event-based fluctuations, or you could incorporate an additional “holiday” or “event” component in your mixture model. If the change is permanent, you must eventually retrain the GMM to reflect the new state.

• Possible Solutions:

  • Incremental or Online EM: Use streaming variants of the EM algorithm that update mixture parameters in small batches as new data arrives. This reduces the time between updates and allows you to adapt more quickly.

  • Mixture of Experts: Instead of one global GMM, you can maintain multiple GMMs each specialized to different time segments or usage scenarios, then pick or weight them based on current conditions.

  • Prior Knowledge about Seasonal Patterns: If you have historical data showing consistent shifts during specific times (e.g., daily or monthly cycles), you can incorporate that knowledge. One approach is segmenting data by time-of-day or day-of-week, training separate submodels, or using time as an additional feature in your GMM.

• Potential Pitfall: Overreacting to short-term noise. You might see a spike in certain types of transactions and rush to retrain. If that pattern subsides quickly, the new model might underfit or misrepresent the typical distribution.

How do we handle situations where some transaction features are missing or incomplete for certain records?

In real-world financial data, not all features are always available: a customer might not provide certain optional information, or some data might be lost due to system errors. GMMs, by default, assume complete vectors for each data point. Missing data can complicate both training and inference.

Detailed considerations:

• Imputation Approaches:

  • Mean/Median Imputation: A simple strategy is to fill missing feature values with the mean (for continuous features) or the most common category (for categorical features). This can, however, artificially reduce the variance and might bias the GMM parameters.

  • Multiple Imputation or Regression-Based Imputation: A more sophisticated approach involves estimating the missing feature using a regression or model-based method. For instance, you could train a regression model on available features to predict the missing feature. This is more accurate but also more computationally intensive.

  • EM with Missing Data: In principle, the EM algorithm for GMM can be extended to handle missing data by treating missing values as latent variables. Each E-step would include an expectation over the missing features. This is more mathematically involved and not always readily available in off-the-shelf libraries.

• Pitfall of Simplistic Imputation: If missingness is not random (e.g., certain features are missing systematically for fraudulent cases), naive imputation can distort your distribution or reduce the model’s ability to detect anomalies. Sometimes, the very fact that a feature is missing can be indicative of higher fraud risk.

• Practical Workarounds:

  • Indicator Variables: Add a binary indicator feature that flags whether the original feature was missing. The GMM then can learn if the pattern “feature is missing” correlates with certain cluster behavior. However, you must handle the actual missing value in some numeric manner (imputation or specialized approach).

  • Discarding Incomplete Records: This is the simplest approach but can severely reduce your training data size and potentially remove important anomalies (since fraudulent transactions might be more likely to be incomplete). Generally, discarding data is a last resort if missingness is too extensive or the fraction of missing data is small.

How can we incorporate temporal or sequential dependencies in transaction data when using GMMs?

Transactions often arrive in a temporal sequence—fraudsters might exploit patterns over time, or legitimate users might have session-based activity. A plain GMM assumes independent samples, ignoring these time dependencies.

Key points:

• Sequential Nature of Fraud: Some fraud attacks exhibit bursts of anomalies over short time windows. Others might show an evolving pattern across days or weeks. A static GMM that treats each transaction as i.i.d. can miss those temporal clues.

• Hidden Markov Models (HMM): One classic extension is to use an HMM, where each latent state could be modeled as a Gaussian distribution (or GMM substate). This is more complex to train but naturally handles sequences. In a fraud setting, you might have states that represent “legitimate sequence of purchases” vs. “suspicious activity over time.”

• Feature Engineering for Time: Another simpler approach is to add derived time-related features into the GMM. For instance, you might incorporate “time since last transaction,” “hour of day,” or “transaction frequency in the last 24 hours.” The GMM then partially captures temporal patterns if these features strongly correlate with anomalies.

• Potential Issue of Non-Stationarity: If the process evolves significantly over time (like concept drift), an HMM or GMM might still become stale unless updated regularly.

• Data Scalability: Modeling full sequences can become expensive for large volumes of transactions. Typically, you might break sessions or short windows of transactions and represent them by summary statistics or embeddings, then feed those to a GMM.

How do we interpret the GMM mixture components from a domain perspective to explain anomalies to stakeholders?

GMMs often have many parameters (means, covariances, mixing coefficients). Explaining why a transaction is low-likelihood can be challenging, especially to non-technical stakeholders.

Detailed breakdown:

• Component Proximity: One interpretability approach is to identify which component (or components) have the highest posterior probability for a given transaction. Then analyze how that component’s mean vector and covariance compare to the transaction’s features. Stakeholders might see “You are close to the cluster with large daily spending on groceries, small weekly spending on electronics…” vs. “This transaction is far from any known cluster.”

• Relative Feature Deviations: For an anomaly, you can measure how many standard deviations away (in Mahalanobis distance terms) the transaction is from the nearest component’s mean. This reveals which features are most responsible. If the user typically buys items < $100, but suddenly a $10,000 jewelry purchase appears, that dimension stands out.

• Combining GMM with Domain Rules: Sometimes domain rules can label clusters. For instance, you might discover that cluster #2 corresponds mostly to “frequent travelers,” cluster #3 is “stay-at-home parents,” etc. Then you can explain anomalies by referencing these known profiles. This labeled component approach helps non-technical reviewers grasp the rationale for flagging.

• Potential Pitfall: Overfitting or unrealistic clusters. A GMM might produce a cluster that doesn’t make intuitive sense if the data is highly complex or multi-modal with partial overlaps. Interpretation then becomes confusing or contradictory. Always verify cluster meaning with domain experts if possible.

How do we address highly imbalanced cost structures, where false negatives (missed fraud) are extremely costly compared to false positives?

Fraud detection often has an imbalanced cost scenario: letting a fraudulent transaction through can be very expensive, but occasionally inconveniencing a user might be less costly. A standard GMM with a single threshold may not reflect these asymmetric costs well.

Approaches:

• Cost-Sensitive Thresholding: Instead of picking a threshold that yields, say, 95% TPR with 5% FPR, you directly incorporate cost into the threshold selection. You can define a cost function such as

  

  

  Weighting Data Points: Some advanced EM implementations might let you weight each data point based on its importance. However, in an unsupervised setting, you typically do not have direct labels to weigh. If you have partial labeled fraud data, you could give fraudulent points higher weight to ensure the GMM tries to fit them or isolate them distinctly, though this changes the fundamental assumption of modeling normal data only.

• Two-Tiered System: You might keep a relatively lenient threshold to detect suspicious transactions and pass them to a secondary, more complex or more expensive check. This multi-stage approach can reduce the incidence of missed fraud while not overwhelming the system with false positives at scale.

• Edge Case: If the cost of a missed fraud is extremely high, you might set the threshold so low that you flag an enormous portion of normal transactions. This can generate a deluge of false positives and actually hamper investigations. Balancing the scale of investigations vs. the risk of missed fraud is always a trade-off requiring domain input.

Is the GMM approach scalable for extremely large datasets or streaming data? What are practical techniques to handle large volumes?

Many financial institutions handle millions of transactions daily. A standard EM algorithm for GMM can become computationally expensive in both time and memory, especially if we use full covariance matrices and large K.

In-depth:

• Mini-Batch or Online GMM: Similar to how mini-batch algorithms exist for k-means, you can implement or use an online EM variant that updates parameters incrementally as data arrives. This lowers memory usage and can adapt to streaming data.

• Approximation Techniques: Variational inference can be used for large-scale mixture modeling. You approximate the posterior distributions of parameters, and it can be more efficient than classical EM in some scenarios.

• Dimensionality Reduction: High-dimensional data (e.g., hundreds of features) can make the covariance estimation for each Gaussian quite large. Reducing to a smaller latent space (via PCA or autoencoders) first, then fitting a GMM, can dramatically lower computation.

• Clustering Preprocessing: Another strategy is to do a coarser clustering (e.g., k-means) on large data to form “super-points,” each with an assigned weight (the cluster size). You then run a GMM on these weighted cluster centers. This is an approximation but can handle massive datasets more efficiently.

• Edge Case: If the data arrives in a real-time stream, you have limited time to do even mini-batch EM. You might consider simpler density estimators or specialized streaming algorithms. Also, the concept drift factor becomes crucial; you may need to continually discard old data as it becomes less relevant.

How do we incorporate external knowledge about known fraudulent methods or handcrafted rules into a GMM-based anomaly detection system?

Fraud detection often benefits from domain expertise: banks might know certain merchant codes or transaction flows are historically problematic. A pure data-driven GMM might not automatically prioritize those.

Mechanisms for integration:

• Feature Engineering: Encode known risk signals as additional features (e.g., “transaction with high-risk merchant code,” “unusual location,” or “account age is less than 1 week”). The GMM then sees these signals within its distribution. Points with strongly suspicious feature values might end up in lower-likelihood regions more easily.

• Post-Filter or Hybrid System: Even if the GMM does not explicitly encode the rule, you can create a post-processing step. For instance, if the GMM flags a transaction as borderline but a rule triggers a high-risk merchant category, you can escalate the score. Or if a transaction is extremely safe by domain knowledge, you might reduce false positives by adjusting the final decision.

• Semi-Supervised Extension: If some known fraud patterns exist (like a certain merchant code that is almost always fraudulent), you could build a separate “fraud component” to capture those patterns. This requires enough data to estimate that component. Alternatively, you can forcibly label those patterns as fraudulent and not rely on GMM’s unsupervised approach alone.

• Potential Pitfall: Over-reliance on domain rules that might be outdated. Fraud patterns evolve, so purely rule-based flags might become stale. Balancing between dynamic GMM detection and static domain knowledge is key.

What if the anomalies are very subtle and lie close to normal points in the feature space?

Sometimes fraudsters try to mimic normal behavior as closely as possible, so the distribution of fraudulent transactions can partially overlap with legitimate transactions, making it difficult for a GMM to separate them.

Considerations:

• Density Overlap: The GMM might give a moderately high likelihood to these subtle fraud cases if they look nearly normal on most features. As a result, they won’t be flagged by a simple threshold on log-likelihood.

• Richer Features or Granularity: Potential solution is to find more discriminative features that highlight subtle differences, such as device fingerprinting, advanced location checks, or anomalies in typical spending intervals. If your current feature set does not differentiate these subtle anomalies, no purely density-based approach can reliably flag them.

• Multi-Stage System: A GMM might serve as a coarse filter. Transactions that are borderline are further analyzed by more sophisticated or supervised methods. In some real pipelines, the GMM score is combined with a specialized classifier that attempts to pick out subtle patterns.

• Edge Case: If your normal distribution is extremely wide or has multi-modal structure that includes the subtle fraud region, the GMM might “explain away” the fraud. In such cases, you may want partial labeling or sample suspicious points for a separate model to learn finer distinctions.

How do we handle a scenario where legitimate transactions vastly outnumber fraudulent ones?

Imbalanced data is typical in fraud detection. The GMM approach usually estimates the distribution of the majority class (legitimate). However, if the fraction of fraud data is minuscule, you risk overshadowing its presence when training a GMM that includes fraud clusters.

Strategies:

• One-Class Approach: Train the GMM or a one-class model purely on legitimate transactions, ignoring fraud data during training. Then use a threshold on the likelihood. This approach focuses on capturing “normal” distribution rather than learning explicit fraud clusters.

• Weighting the Fraud Data: If you do want to incorporate known fraud data, you might artificially upsample or assign higher weights to fraudulent samples in the EM procedure. This ensures the model tries to create at least one “fraud” cluster that is distinct. However, if real fraud is extremely diverse, a single cluster might not suffice.

• Multiple Metrics beyond Thresholding: Because of the extreme imbalance, you need to consider metrics like Precision-Recall or cost-based analysis rather than standard accuracy. A 99.99% overall accuracy might hide the fact you are missing a large fraction of the very few fraud cases.

• Pitfall: Overfitting to limited fraud examples. If you only have a handful of fraud samples, the GMM might learn spurious means and covariances for that cluster. Also, new or unseen fraud patterns might be missed altogether.

How do we handle highly nonstationary data with repeating daily or weekly cycles, in addition to random changes?

Financial transactions often exhibit regular cyclical patterns (e.g., daily usage peaks, weekend vs. weekday differences). This cyclical nature can get muddled with random fluctuations or longer-term drift.

Insights:

• Time-of-Day/Day-of-Week as Features: By adding cyclical time features (like sine and cosine transforms of the hour of day or day of week), the GMM might learn distinct clusters for morning vs. evening behavior, weekday vs. weekend spending, etc.

• Seasonal GMMs: Another approach is to maintain separate GMMs for different known cyclical periods: one for weekdays, one for weekends, or more granular splits. This might better capture the normal pattern within each sub-period.

• Update Frequency: If cyclical patterns shift over months, you need to retrain or adjust the GMM periodically. You might track rolling windows of data so the model stays aligned with the most recent cycle.

• Edge Case of Overlapping Cycles: Real data can have multiple cycles, e.g., daily plus monthly. If your features do not capture these effectively, the GMM might create many small clusters just to fit day-to-day differences, hindering interpretability. Carefully designed time features or domain decomposition can help keep the model from over-segmenting.