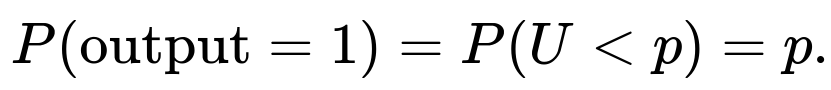ML Interview Q Series: Generating Biased Bernoulli Trials From Unbiased Bits Using Binary Expansions

Browse all the Probability Interview Questions here.

12. Given a generator of unbiased Bernoulli numbers (0 or 1 with p=0.5), create a biased Bernoulli trial generator (generate 0 or 1 with a specified 0 < p < 1).

One way to construct a biased Bernoulli random variable from an unbiased one is to interpret the sequence of unbiased bits as a binary expansion of a random number in the interval [0,1). Then compare that random number to the target probability p. If the generated number is less than p, output 1; otherwise, output 0.

Below is a deeply detailed explanation of how and why this works, plus a Python code example. Afterwards, there are several follow-up questions that an interviewer might ask to test nuanced understanding of the method and its practical considerations, together with thorough answers.

Creating A Biased Bernoulli Generator

Understanding The Core Idea

We have an unbiased Bernoulli generator that outputs 0 or 1 with probability 0.5 each. Each output is often referred to as a random bit. If we collect enough of these bits, we can interpret the sequence as a random number in binary form. For instance, if we draw three unbiased bits b₁, b₂, b₃, we interpret it as a binary fraction:

This is a random number uniformly distributed in [0,1) (in practice, if we only collect k bits, we have a discrete uniform distribution over the set {0, 1/2^k, 2/2^k, …, (2^k - 1)/2^k}). If we compare this random number to some fixed p (0 < p < 1), the probability that this random number is less than p is exactly p, which gives us the biased Bernoulli trial. The reason is that uniform draws in [0,1) land below p with probability p.

When p is a rational or irrational number, the same principle holds. The typical real-world implementation just uses floating-point arithmetic to compare a floating uniform sample to p. The difference here is that we do not have a direct floating uniform sample. Instead, we have an unbiased coin that can produce bits. The bits can be collected and interpreted to approximate a uniform random value in [0,1), and then we compare.

Explicit Bit-By-Bit Comparison In Binary

Conceptually, you can also do a bit-by-bit comparison with p written in binary form, 0.p₁p₂p₃… If you generate your random bits 0.r₁r₂r₃… and compare them bit by bit to 0.p₁p₂p₃…:

• If at some step i, we find rᵢ < pᵢ, we decide the random number is below p and output 1. • If at some step i, we find rᵢ > pᵢ, we decide the random number is above p and output 0. • If rᵢ = pᵢ, we proceed to the next bit and keep comparing.

In practice, one must handle the possibility that p has an infinite binary expansion. However, one can keep generating more bits from the unbiased coin generator until we can make a definitive decision (or decide on some approximation). This ensures that even if p is irrational, we can still eventually reach a conclusion with probability 1.

Implementation in Python

Here is a simple demonstration using Python. We assume we have a function flip_fair_coin() that returns 0 or 1 with probability 0.5 each.

import random

def flip_fair_coin():
    # This simulates our unbiased Bernoulli generator
    return 0 if random.random() < 0.5 else 1

def generate_biased_bernoulli(p):
    """
    Generate a single Bernoulli( p ) sample using only flip_fair_coin(),
    which is Bernoulli(0.5).
    """
    # We choose a suitable number of bits, say 32 for typical single-precision.
    # For higher precision, we can use more bits.
    num_bits = 32

    # Collect the bits as an integer in [0, 2^num_bits - 1].
    value = 0
    for i in range(num_bits):
        bit = flip_fair_coin()  # 0 or 1 with probability 0.5
        value = (value << 1) | bit

    # Interpret value / 2^num_bits as a floating number in [0,1).
    uniform_approx = value / (2 ** num_bits)

    # Compare to p
    return 1 if (uniform_approx < p) else 0

# Example usage:
n_trials = 100000
p_desired = 0.7
count_ones = 0

for _ in range(n_trials):
    outcome = generate_biased_bernoulli(p_desired)
    count_ones += outcome

empirical_prob = count_ones / n_trials
print("Empirical probability of 1:", empirical_prob)

In the above approach:

• We used flip_fair_coin() as our source of unbiased bits. • We combined 32 bits to form an integer in the range [0, 2³² - 1]. • We then divided by 2³² to get a number in [0,1). • We returned 1 if the resulting fraction is less than p; otherwise, we returned 0.

This method can be extended for more or fewer bits depending on the precision requirements or performance considerations.

Potential Pitfalls and Edge Cases

• Precision: If p is extremely close to 0 or 1, a 32-bit fraction may or may not be sufficient for accurate results in some edge cases. In practice, 32 or 64 bits are usually more than enough for single or double-precision floating-point. • Irrational p: If p is not representable exactly in a floating format or if it is irrational, we still approximate it. The more bits we generate, the more accurate our uniform sample. • Efficiency Concerns: Generating too many bits might slow down the process if you need a high-throughput generator. But it ensures a more precise outcome. • Binary Expansion Approach: If we do a bit-by-bit comparison to an infinite binary expansion of p, we might generate bits for a long time if the random fraction is extremely close to p. This happens with probability zero in theory, but in practice one handles floating approximations or sets a maximum number of bits.

Now we explore likely follow-up questions in a tough interview and answer them in detail.

If p is extremely close to 0 or 1, do we risk numerical issues or infinite loops in the bit-by-bit method?

Yes. When p is very close to 0 or 1, you will often figure out the correct result quickly, not slowly. Specifically:

• If p is extremely close to 1, then the random fraction 0.r₁r₂r₃… typically will be less than p, so you quickly determine the outcome is 1. • If p is extremely close to 0, then the random fraction is typically going to exceed p, so we quickly determine the outcome is 0. • The worry about an infinite loop might arise if the random fraction is extremely close to p, but that event has probability 0 in continuous theory. In practice (with finite-bit approximations), you eventually terminate.

In the bit-by-bit method, you normally would set a safe maximum number of bits to generate. That maximum ensures you do not get stuck if p has a complicated binary expansion and the random fraction is also extremely close to p. After that maximum, you can break and approximate. With typical floating-point usage, you automatically have a limit (like 64 bits if you are using double precision) and do a straightforward comparison.

How can we handle irrational values of p that do not have a terminating binary expansion?

Any irrational number p has a non-terminating, non-repeating binary expansion. You do not have to store all bits of p. Instead, you generate your random fraction’s bits on the fly and compare them bit by bit to p’s bits (also computed on the fly, using partial expansions). In actual implementations:

• You might store an approximate binary representation of p to some fixed precision (like a double precision float or a binary fraction with 64 bits). • You generate your random bits up to the same precision. • Once you have either conclusively compared or run out of bits, you decide.

If you must exactly handle an irrational p, you do a lazy evaluation approach: produce bits of p by repeated multiplications by 2 and checking if the integer part is 1 or 0. Each step yields one bit of p in binary. You compare that bit to the random bit. Continue until they differ, or you decide to stop after some large finite limit. The chance of going on indefinitely is effectively zero with continuous distributions.

Is there a more direct or simpler method if we can already generate uniform(0,1) random numbers?

Yes. If the programming environment already offers a uniform(0,1) generator, we can just do:

import random

def biased_bernoulli(p):
    return 1 if random.random() < p else 0

But the original question posits that we do NOT have a built-in uniform(0,1) generator. Instead, we only have an unbiased Bernoulli(0.5) generator. To simulate a uniform(0,1) random variable, we gather bits from the unbiased coin. This is effectively the same as using random.random() in Python but is spelled out explicitly in a purely “bit-based” scenario.

What if we need infinite precision or a fully exact method?

A fully exact method for rational p = a/b can be done using integer arithmetic, but it can become slower if b is large. One approach is:

• Generate enough bits to produce an integer K in [0, 2^m) so that 2^m ≥ b. • Compare K with ⌊p * 2^m⌋ = ⌊(a/b) * 2^m⌋. • If K < ⌊(a/b) * 2^m⌋, return 1; else return 0. • If 2^m is exactly a multiple of b, you can do an exact integer comparison (like K < (a * 2^m/b)).

In the irrational case, you typically do not get a purely “exact” integer method. Instead, you do the bit-by-bit approach in principle. In the real world, we usually settle for high-precision floating approximations.

What is the time complexity?

If you gather a fixed number of bits (e.g., 32 or 64) and do a single comparison, the time complexity is O(k) where k is your chosen number of bits. In a bit-by-bit approach that potentially continues until it can decide, the expected time is still finite because the probability that the random fraction matches exactly the partial expansion of p for too many bits is extremely small. Typically, you expect to terminate quickly once the bits differ.

Is there a known name for the bit-by-bit method comparing expansions?

Yes. It is sometimes referenced as the “BBP-like method” (pertaining to spigot or digit-extraction approaches) or more commonly, “Algorithmic Bernoulli Trials via Bit-Comparison,” which is an outgrowth of the classical approach for generating a uniform random in [0,1). This concept is more generally a known technique in the realm of generating random variables from discrete coin flips.

How would you prove correctness?

The fundamental proof of correctness is that if bits are unbiased and independent, then any integer in [0, 2^k) is equally likely, giving a uniform distribution over that discrete set. Interpreted as a fraction in [0,1), it approximates a uniform random variable. Comparing with p yields a Bernoulli random variable with parameter p. The limiting process as k → ∞ yields an exact Bernoulli(p). Formally:

• For each integer x in [0, 2^k - 1], probability is 1 / 2^k. • Probability(x < ⌊p * 2^k⌋) = ⌊p * 2^k⌋ / 2^k ≈ p. • As k → ∞, ⌊p * 2^k⌋ / 2^k → p.

Hence, the outcome tends to a Bernoulli with parameter p.

Could this be used to generate non-Bernoulli distributions?

Yes. Once you can generate a uniform random number in [0,1) from unbiased bits, you can transform it using standard techniques (inverse transform sampling, acceptance-rejection, etc.) to produce any distribution. For a Bernoulli specifically, we only do a threshold check. For more complicated distributions, we can do more sophisticated transformations.

What if someone suggests Von Neumann’s extractor method? Is that relevant here?

Von Neumann’s extractor is typically used for the opposite scenario: you have a biased coin and want to produce an unbiased coin. Here, we have an unbiased coin and we need a biased coin. Von Neumann’s technique is not required. The problem is easier in this direction: generating a biased outcome from an unbiased coin is straightforward. Von Neumann’s approach is more famously used to remove bias if your coin flips come from an unknown p ≠ 0.5.

Are there any practical concerns about speed?

Yes. Although the concept is straightforward, in practice you often rely on well-tested uniform pseudo-random number generators at the hardware or library level. These are typically optimized in CPU instructions or GPU pipelines. Doing it bit-by-bit in Python could be slow for very high throughput scenarios. For typical usage, modern languages provide random floats in [0,1) that are effectively the same as collecting bits from an unbiased source. The method is more of a conceptual demonstration of how to do it when you only have an unbiased coin flip at a very low-level interface.

Could we ever produce a sample with probability exactly p = 0.37 or any other real number?

Yes, any real 0 < p < 1 can be approximated to as many bits as desired. In practice, your environment might store p in a finite precision float or double, so you do a finite approximation. That yields a Bernoulli random variable with parameter extremely close to p. If you need exact rational p = a/b, you can do exact integer-based comparisons as described previously. For an irrational p, one can do the infinite expansion approach in principle. In real applications, we almost always do a finite approximation.

How would you verify your code is producing the correct biased distribution?

One standard approach is to run many trials and observe the empirical frequency of 1 vs. 0. You can do a statistical test such as a chi-square test or a binomial proportion confidence interval to see if the proportion of 1’s converges to p within some margin of error. For instance, if you run 100,000 trials for p=0.7, you’d expect around 70,000 ones. Then you can confirm that’s within a statistically reasonable range for a binomial(n=100000, p=0.7).

If the empirical proportion consistently deviates significantly from the target p, there might be bugs in how the bits are collected or compared.

Could we combine partial sums of bits to speed things up?

Yes. For instance, you can generate k bits at once to form an integer K. Then compare K with some threshold T = ⌊p * 2^k⌋. If K < T, output 1; else if K > T, output 0; else if K = T, you can continue generating more bits. This approach is akin to the bit-by-bit method but lumps multiple bits at a time for efficiency. Often, you just do a one-shot with k = 32 or 64 bits and then do a floating comparison. That’s typically the fastest for practical code.

Is there a direct closed-form expression for the probability that the generated variable is 1?

Yes. If you interpret the collected bits as a uniform random variable U on [0,1), then:

That’s precisely the definition of Bernoulli(p). The entire method is built so that U is uniform in [0,1), thus ensuring that probability is p.

Why not just multiply random bits by weights and compare the sum to p?

In principle, generating bits and summing them with geometric weights is precisely how you form the binary fraction. Interpreting them as a floating number is just a succinct way to do that. Summing bits as 2^{-i} for bit i is effectively building the fraction 0.r₁r₂r₃… in binary. Doing it in a single integer accumulation and dividing by 2^k is just a neat implementation shortcut.

What if we want a whole random integer in [0, n-1] with probabilities set by custom distribution?

Although not asked directly, it’s a close extension. If you can produce Bernoulli(p), you can also produce categorical distributions in principle. Usually, you do a similar approach: generate enough bits to produce a uniform integer K in [0, 2^m), then map that integer into the distribution intervals. If distribution categories are not powers of two in size, you can do acceptance-rejection or other ways to handle leftover integer values. Or you can do a sequential threshold approach: compare to p₁, if less, choose category 1, else compare to p₂ / (1 - p₁), and so on.

All these possible follow-ups connect back to how collecting unbiased bits is a flexible foundation for building many random distributions, with Bernoulli(p) as the simplest threshold example.

Below are additional follow-up questions

What if the coin flips are not perfectly independent in practice?

Even though we theoretically assume the coin flips (or bits) from the unbiased generator are independent, real-world hardware or physical processes may introduce slight correlations between consecutive flips. For example, if there is some electrical noise pattern or a hardware defect, the coin flips might not be strictly uncorrelated. This can affect the distribution of our final Bernoulli(p) in subtle ways.

To analyze this:

• If the correlation is small, over many flips, the law of large numbers might still produce approximately unbiased bits. The small correlation might not dramatically change the overall distribution, but in rigorous cryptographic or high-precision applications, it could be problematic. • If the correlation is large enough that the bit sequence drifts away from uniformity, then your final distribution might systematically deviate from p. For instance, if the hardware is more likely to produce consecutive identical bits (00 or 11), your uniform fraction in [0,1) might not be perfectly uniform anymore. • One technique is to test your coin with statistical randomness tests (e.g., Diehard tests or NIST tests) to gauge the correlation or bias. If a correlation is detected, you might need to whiten or decorrelate the bits (e.g., by passing them through an extractor or corrector) before using them to generate the Bernoulli(p).

Potential pitfall is that a user might rely heavily on the assumption of independence without empirical testing. In mission-critical scenarios (like cryptographic or gambling applications), verifying independence with thorough testing is essential.

Could we optimize for repeated generation if we need many samples from the same p?

When generating a large number of Bernoulli(p) samples, repeatedly doing a 32- or 64-bit approach for each trial may be slightly inefficient. A few strategies can help:

• Batch Generation Instead of generating one uniform fraction per sample, you could generate a large random integer once and harvest multiple Bernoulli draws from the bits. For example, if you generate 64 random bits, you can interpret them as multiple smaller uniform numbers or partial expansions. However, you must be careful to ensure that each subset of bits you carve out is used in a manner that remains unbiased.

• Table Lookup Approach If p is fixed, you could consider an approach like generating multiple bits at once (e.g., 8 bits = 256 possible outcomes) and storing how many of those 256 patterns lead to “1” and how many to “0.” You’d do acceptance-rejection if you exceed the portion allocated to “1.” This becomes complex but might speed up if you do a lot of draws.

• Streaming Approaches If you do a bit-by-bit comparison to p’s binary expansion, you might find that on average you don’t need all 32 or 64 bits to make a decision, especially if p is either large or small. The expected number of bits might be significantly lower. This can be more efficient in average-case scenarios but might be more complex to implement.

A subtle pitfall is that if you try to reuse partial bits from one trial for the next, you have to ensure the leftover bits don’t compromise uniformity or independence. For instance, if you used 17 bits out of a 32-bit chunk for the first Bernoulli draw, you might be tempted to use the remaining 15 bits for the next. But you have to track them carefully to ensure correct uniform distribution for that subsequent fraction.

Can the method get stuck if the random fraction is exactly p in binary form?

In an idealized continuous sense, the probability that a uniformly chosen real number in [0,1) is exactly equal to p (which itself might be an irrational or rational with an infinite binary expansion) is zero. That means, with probability 1, you will eventually discover that your fraction is either less than or greater than p. In practice, with floating-point or finite-bit expansions, you handle this by:

• Generating only a finite number of bits (e.g., 64). Then you compare the 64-bit approximation of the fraction to the 64-bit approximation of p. If they are exactly equal, you might do a tie-break or generate more bits. However, the chance of an exact tie in the finite-bit representation is generally extremely small unless p is exactly a dyadic fraction with denominator 2^k. • Setting a maximum iteration count for the bit-by-bit method. If you are still “tied” after, say, 64 or 128 bits, treat that as effectively equal. You could randomly choose 0 or 1 in that situation or do a refined procedure if you want.

Therefore, the method almost never truly “gets stuck,” but you do need an escape hatch in an implementation that strictly does bit-by-bit comparison. A real-world pitfall is forgetting to handle the tie condition and letting the code loop infinitely.

Is there a minimal-expected-number-of-coin-flips algorithm for Bernoulli(p)?

Yes, there is a known approach—an optimal or near-optimal coin-flip method for Bernoulli(p)—that tries to reduce the expected number of unbiased coin flips. For rational p, one can use a sequential approach known as the Grenander’s method or a more general technique from the theory of optimal Bernoulli factory algorithms. The idea is to exploit early termination:

• You generate bits in a way that if a partial sequence strongly indicates the sample is below or above p, you decide immediately. • Only in borderline scenarios do you continue generating more bits.

For example, a simple version:

1. Write p in binary up to a large number of bits.

2. Compare bits of the random fraction to bits of p from left to right.

3. If at step k you see the fraction is definitely less or definitely greater, you decide early and stop.

This leads to an expected number of flips that can be significantly less than 64 in many cases, especially if p is near 0 or 1. However, the distribution of the number of flips can be long-tailed if p is near 0.5. A practical pitfall is complexity: implementing this precisely might be more complicated than just generating all 32 or 64 bits at once.

What if p changes from trial to trial?

In some applications, you need Bernoulli draws with varying p for each sample (e.g., p depends on features in an online algorithm). You then can:

• Generate each trial’s fraction anew: gather 32 or 64 bits, form a uniform random, compare to the current p. This is straightforward but might be slower if you do it frequently. • If you do bit-by-bit expansions, you must re-compute or have a stored binary expansion for each p. For many different p values, you might do a dynamic approach where you compute partial expansions on the fly: multiply p by 2, compare integer part, subtract that out, continue.

Potential pitfalls:

• You have to handle floating precision for each new p. If p is coming from some real-time stream or your model outputs p as a floating value, you just do the standard approach each time. • If you keep many expansions of p in memory, it can become large if you need high precision for many distinct p’s.

What if the device generating the bits is only “approximately” unbiased?

If the device is not guaranteed to be perfectly 0.5–0.5, but maybe 0.5±ε for some small ε, then your uniform fraction is not truly uniform. This means your final Bernoulli(p) is not exactly Bernoulli(p). The question is whether the small bias accumulates or if you can correct it:

• Small Deviation If ε is tiny, the final distribution might be close to Bernoulli(p). In many practical scenarios, that might be acceptable if ε is extremely small. • Exact Correction There are techniques (related to the Von Neumann extractor idea, but extended) that can convert a coin of unknown p into an unbiased coin. Then from that unbiased coin, we produce the desired Bernoulli(p). However, these methods can be complicated and might reduce throughput.

Pitfalls:

• Failing to realize that an “approximately unbiased” coin with p=0.5+ε could cause a significant error in the final distribution if you generate a large number of bits and combine them. • Believing that small biases automatically vanish upon combination is incorrect. They can amplify or shift the distribution in ways that are not trivial unless you properly correct or account for them.

Does this approach scale well in a parallel computing environment?

In a parallel or distributed scenario, you could replicate the process on multiple threads or machines:

• Each thread or machine has its own unbiased coin flips. It accumulates 32 or 64 bits, forms a uniform fraction, compares to p, and outputs the result. This parallelizes nicely since each Bernoulli draw is independent. • You just need a reliable way to ensure that each thread gets truly independent bits. If your random seed or hardware source is compromised or repeated, that can create correlations across threads.

Edge cases might arise if threads share a random bit generator. You must either partition the bit stream carefully or give each thread a separate random stream. If you fail to do so, you might end up with correlated or repeated samples in different threads.

How do we handle guaranteed maximum error bounds with a finite number of bits?

If p is an irrational or non-terminating binary fraction, any finite-bit approach only approximates it:

• With k bits, the uniform sample is in increments of 1 / 2^k. This means we can be off by at most 1 / 2^k in the threshold that splits 0 vs. 1. • If you want a guaranteed bound such as the final distribution must differ from Bernoulli(p) by at most δ in total variation distance, you can choose k large enough so that 1 / 2^k < δ.

Pitfalls include:

• Overestimating or underestimating how big k must be to ensure a certain error margin. • Mistaking floating-point rounding error as the only source of error. In reality, if p is represented in double precision, that also limits your accuracy.

In typical practice, 32-bit or 64-bit precision is more than enough for most tasks unless you are in a domain like cryptography or extremely high-precision Monte Carlo simulations.

Could we store partially used random bits from one trial to use in the next?

Sometimes, you might generate more bits than needed if your bit-by-bit approach terminates early. For example, you might read a chunk of 64 bits, but you only actually used 10 bits before deciding the outcome. In principle, you could store the remaining 54 bits for future trials:

• This can be efficient because you do not want to waste bits that you already drew from the hardware generator. • However, you must carefully track exactly which bits remain unused so that each new fraction is properly formed from fresh or leftover bits.

A subtle pitfall is if you partially used bits in a way that ties the leftover bits to the partial decision you already made, it might break the independence assumption for the new fraction. The safer approach is to read bits in smaller increments only as you need them. That can be slower in practice if your hardware random generator or system library provides random bits in large blocks (like 64 bits at a time).

What if we want to generate correlated Bernoulli variables instead of independent ones?

The approach described focuses on generating a single Bernoulli(p) that is marginally distributed with probability p. If you want multiple Bernoulli variables with correlation (e.g., a certain joint distribution), you can:

• Generate a uniform(0,1) fraction from the unbiased bits. • Use an appropriate transform that produces correlated Bernoulli outcomes. For instance, you can sample from a bivariate or multivariate distribution that has the desired correlation. • One simple example: to produce X and Y with some correlation, you might generate one uniform(0,1) to decide X, then condition on X for Y. This usually involves more advanced sampling steps.

Pitfalls:

• Generating correlated random variables is not as simple as just comparing the same fraction to different thresholds, because that would not produce correlation (it could produce some patterns, but not general correlation). • Ensuring the correct correlation structure might require a more elaborate method (e.g., a copula-based approach or an exact discrete method that enumerates probabilities for each outcome pair).

In short, the single coin-flip method extends to correlated draws only if you incorporate additional logic that goes beyond a single threshold test.

Could we use a look-up table or precomputation approach for certain common values of p?

Yes, if you frequently need Bernoulli(p) for a small set of known p values:

• You could precompute thresholds for certain bit lengths. For example, for p = 0.3, you store T₃₂ = ⌊0.3 * 2^32⌋, T₆₄ = ⌊0.3 * 2^64⌋, etc. Then generation is simply:

1. Generate 32 (or 64) bits.

2. Form an integer K.

3. Compare K with T₃₂ (or T₆₄). • This saves time if you do the same p repeatedly.

However:

• If you have many possible p values, a lookup might be too large. • If p changes rapidly, precomputation doesn’t help much. • You must ensure the integer thresholds are computed carefully to avoid rounding errors in floating arithmetic.

Could floating-point overflow or underflow be an issue if p is extremely small or large?

When we talk about p being close to 0 or 1, typical double precision can handle p ~ 1e-308 for underflow in some contexts, but actually comparing a uniform fraction to 1e-308 might produce numerical anomalies if you do the fraction in a naive floating-point way. However:

• If you generate a 64-bit integer K and do integer math, you do T = ⌊p * 2^64⌋. If p is near 1e-308, T might be 0 for typical double conversions. This effectively means your Bernoulli outcome is almost always 0. • Conversely, if p is near 1 - 1e-16, T might be extremely close to 2^64. This is effectively always 1.

In practice, if you truly need to handle extremely tiny or extremely large p, you might use extended precision arithmetic or a specialized approach. A real pitfall is that for p so small that ⌊p * 2^64⌋ = 0, you will always get 0, which is correct for extremely small p if your 64-bit fraction cannot detect that difference at all. But if your application demands distinguishing p = 1e-20 from p = 1e-22, you need more bits or an alternate method.

Could we use rejection sampling for Bernoulli(p) in some way?

Although it’s more common to use rejection sampling for continuous or discrete distributions with more complicated shapes, one might try a rejection approach:

1. Generate some number of bits.

2. Construct a fraction.

3. If that fraction is in some region of acceptance, decide the outcome. Otherwise, reject and repeat.

For Bernoulli(p), the simpler method is just direct threshold comparison with the uniform fraction. Rejection sampling would be a roundabout approach. You don’t gain efficiency for a single Bernoulli sample. It can be a fallback if you realize you must handle an unusual scenario (like partial leftover bits). Still, it’s rarely used for Bernoulli.

Pitfall is implementing a complicated acceptance-rejection scheme that is effectively doing the same threshold check behind the scenes. You might end up using more random bits than necessary.

How might we measure the randomness quality of the final Bernoulli(p) distribution in practice?

You could collect a large sample of outcomes and run:

• Empirical Proportion Test Compare the fraction of 1’s to p over many trials—this is the simplest. • Binomial Goodness-of-Fit Under the null hypothesis that the distribution is Bernoulli(p), the count of 1’s in n trials should be roughly Binomial(n, p). You can do a chi-square or a normal approximation test. • Sequential Tests You can check that there’s no suspicious pattern in the sequence of Bernoulli outputs. For instance, if you see too many runs of consecutive 1’s or 0’s, that might indicate something is off with your random generator.

A subtlety is that measuring p accurately requires a large number of trials. If p is extremely small (say 1e-6), you’d need a proportionally large number of samples to accurately estimate that probability. Failing to gather enough data or failing to use a test suited for very small p can produce misleading conclusions.