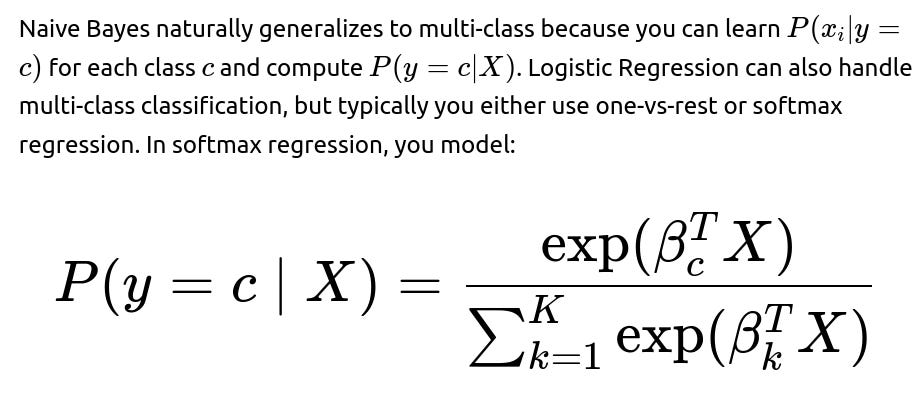ML Interview Q Series: Generative vs Discriminative Classifiers: Contrasting Naive Bayes and Logistic Regression.
📚 Browse the full ML Interview series here.
Generative vs Discriminative Models: Compare generative and discriminative models. For instance, how do Naive Bayes (a generative classifier) and Logistic Regression (a discriminative classifier) differ in what they learn and how they make predictions? In what situations might you prefer a generative model over a discriminative one, or vice versa?
Generative and discriminative models differ in how they conceptualize and approach the classification (or general prediction) task. The central idea is that a generative model attempts to learn a joint distribution of the data (features) and labels, while a discriminative model focuses on directly modeling the conditional distribution of labels given the data.
Generative Model Core Ideas
to predict labels. Because it’s modeling P(X,y) (decomposed as P(y)P(X∣y)), Naive Bayes is considered a generative approach. In practice, it’s straightforward to train, can handle small datasets well, and deals gracefully with missing features (since each feature is treated independently given the class).
Discriminative Model Core Ideas
A discriminative model directly models P(y∣X) or learns a function f(X) that separates data points into classes. It is focused purely on the boundary or direct conditional relationship between X and y, without explicitly modeling how the data points arise. As a result, discriminative approaches can typically yield better classification accuracy when we have ample labeled data, because they do not commit capacity to modeling P(X).
Logistic Regression as a Discriminative Model
Logistic Regression directly learns parameters β that describe the conditional probability of a label y given the features X:
Contrasts Between Naive Bayes and Logistic Regression
Naive Bayes (Generative) tries to learn how each class might generate data. In the presence of strong distributional assumptions (and if these assumptions are fairly correct), it can classify new points by computing P(y∣X) via Bayes’ theorem.
Logistic Regression (Discriminative) bypasses learning how data arises and focuses on the conditional distribution of labels given the features. This often yields superior accuracy under sufficient training data and when the logistic model form is appropriate.
Naive Bayes can be advantageous when: You have small datasets, or certain distributional assumptions hold. Some features can be missing at prediction time (the conditional independence can handle partial features more gracefully). You want to do generative modeling tasks (e.g., data imputation or simulation of data).
Logistic Regression is often preferred when: You have enough labeled data to learn a complex decision boundary. You need higher predictive accuracy in typical classification tasks. You want an interpretable linear boundary that discriminatively separates classes.
Use Cases Where You Might Prefer One Over the Other
When the distribution of data is well-captured by the generative assumptions of the model, or when data is scarce, a generative model like Naive Bayes can sometimes outperform discriminative models. Generative models can also handle missing data more naturally.
When you only care about classification accuracy and have enough labeled data, discriminative models usually perform better because they avoid making strong assumptions about P(X). They focus specifically on how X relates to y.
Generative models can also provide additional capabilities such as sampling new data points, which can be useful in certain settings where you want to generate synthetic data or incorporate unsupervised tasks that rely on P(X). However, if the goal is purely classification and the training set is large, a discriminative approach can be more efficient and yield better performance.
What might a FANG interviewer ask next (Follow-up Questions)?
Why does Naive Bayes often work surprisingly well despite its naive independence assumption?
How do you interpret the decision boundaries produced by Naive Bayes versus those produced by Logistic Regression?
For Naive Bayes, decision boundaries come from comparing which class has the larger posterior probability after applying Bayes’ rule. With two classes, you compute:
[ \huge \ln \frac{P(y=1 \mid X)}{P(y=0 \mid X)} = \ln \frac{P(y=1) \prod_{i} P(x_i \mid y=1)}{P(y=0) \prod_{i} P(x_i \mid y=0)} ]
What if there is strong feature correlation? How does that affect Naive Bayes?
Naive Bayes will tend to overcount or undercount certain probability factors if features are strongly correlated. The fundamental assumption in Naive Bayes is that features are conditionally independent given the class. When that assumption fails (e.g., two features strongly correlate with each other for the same class), the model can overestimate the likelihood. Despite this theoretical drawback, Naive Bayes can remain robust as long as the correlations don’t drastically distort the product of probabilities. Still, if you know in advance that features are heavily correlated, a discriminative model like Logistic Regression or a more flexible method (e.g., random forest) is likely to perform better. Alternatively, you could consider Bayesian networks that represent dependencies among features in a more structured way.
Can you combine the advantages of generative and discriminative approaches?
One way is to train a model like Naive Bayes to capture the generative aspect and a model like Logistic Regression to capture the discriminative decision boundary. You could combine or ensemble predictions from both. Another possibility is to construct a hybrid method (for instance, a semi-supervised approach) that models P(X) generatively but also adjusts parameters discriminatively to optimize classification performance. Techniques such as “Discriminative Naive Bayes” or “Jointly Trained Generative-Discriminative” classifiers have been explored in research, though in large-scale practical systems, practitioners often pivot toward one approach based on data availability and performance requirements.
How do generative models handle missing data more gracefully than discriminative models?
What practical guidelines would you follow to decide between Naive Bayes and Logistic Regression?
You should consider the size of your dataset, the nature of your features, and your objectives: If you have a small dataset and relatively simple feature interactions (or if the independence assumption is not too unrealistic), Naive Bayes is a fast and effective choice. If you have a large labeled dataset, care mostly about predictive performance, and the relationship between features and the label is potentially complex, a discriminative approach like Logistic Regression typically performs better. If you suspect your data generation process can be accurately captured by a specific generative assumption, use a generative approach. If not, discriminative is often safer for pure predictive tasks. If you anticipate missing data at inference time, the flexibility of a generative method might simplify that problem.
How can overfitting or underfitting manifest differently in Naive Bayes versus Logistic Regression?
Logistic Regression can overfit if the number of features is large relative to the number of data points, but regularization methods (like or ) are widely used to mitigate that risk. Underfitting can occur if the relationship between features and outcome is significantly nonlinear or more complex than a linear logit model can capture. In that sense, logistic regression might be prone to bias if the true decision boundary is highly nonlinear and you do not incorporate feature transformations.
What if you want to extend the concepts to multi-class settings?
where K is the total number of classes. The training procedure (e.g., via maximum likelihood) is more computationally intensive than naive Bayes, but not too difficult with modern optimization libraries.
How do the assumptions of Naive Bayes compare with real-world data scenarios?
Real-world data rarely satisfies strict conditional independence among all features. For instance, in text classification, different words in a document can be correlated. However, Naive Bayes can still perform well in bag-of-words text classification tasks because even though words may be correlated, each individual word occurrence strongly correlates with the document topic or class label, which still allows the product of probabilities to produce decent class distinctions. The mismatch between the real correlation structure and the naive independence assumption can degrade performance, but often not enough to outweigh the model’s simplicity and strong bias, especially for smaller datasets or high-dimensional spaces like text.
How would you explain the notion that discriminative models typically outperform generative models when you have “enough” data?
When there is ample labeled data, discriminative models can learn the direct boundary P(y∣X) more effectively because they do not waste modeling power on P(X). Generative models use a portion of their modeling capacity to explain how features arise. If your goal is classification alone, that generative capacity might not directly help in forming a boundary. Additionally, discriminative models allow more flexible parameterizations of P(y∣X), which can better fit complex relationships in the data. However, if the dataset is small, these more flexible parameterizations can overfit, whereas a simpler generative model might generalize better due to stronger assumptions.
How would you briefly summarize when to use a generative model versus a discriminative model?
If you need the ability to generate data, handle missing features seamlessly, or you have very little labeled data and believe your distributional assumptions are not too inaccurate, you might opt for a generative model like Naive Bayes. If you have a relatively larger labeled dataset, want strong predictive accuracy, and only care about P(y∣X), a discriminative model like Logistic Regression is usually preferred. In practice, you often try both or test multiple models to see which yields the best performance on the validation set, unless domain knowledge strongly indicates that one approach’s assumptions or capabilities are more suitable.
Below are additional follow-up questions
How do generative and discriminative models differ in their robustness to outliers or noisy data?
Generative models typically assume an underlying probability distribution for the data. When the training data contains outliers or is heavily noisy, a generative model can be misled if those outliers substantially distort the estimated distribution. For instance, if a small number of extreme points appear in the tail region, and the model fits a Gaussian distribution to the features, these outliers may skew the estimated mean or variance, affecting the joint likelihood in a way that could degrade performance.
Discriminative models, since they focus directly on learning the decision boundary (or P(y∣X)), might be somewhat more robust in scenarios where outliers do not heavily influence that boundary. For example, in Logistic Regression, outliers can affect the gradient-based optimization if they cause large gradient contributions, but modern regularization techniques ( or ) can mitigate their impact. In practice, one would still need to be cautious: if outliers significantly alter the distribution of the training set, even a discriminative model may overfit or find a spurious boundary.
A subtle edge case is when outliers for one class happen to cluster in a region that the model finds highly influential. A generative approach that robustly models the distribution (e.g., with heavy-tailed assumptions) might actually handle this better than a simpler discriminative approach lacking a mechanism for ignoring outlier regions. Conversely, a discriminative model could learn to discount those regions if it finds they do not help separate classes. The final outcome often depends on the type of data distribution assumption in the generative model and the presence or absence of regularization or robust loss functions in the discriminative model.
When might domain knowledge favor a generative approach, and how can we incorporate that knowledge?
If you have deep insights into how the data is generated—such as specific distributions or causal relationships—a generative approach can directly embed that knowledge into the likelihood P(X∣y). For instance, in a medical diagnosis setting, if it is known that certain biomarkers follow a particular distribution given a disease state, you could design a generative model with the appropriate parametric forms. The model can then use those domain-specific distributions for more accurate inference, even with limited labeled data.
One way to incorporate domain knowledge in a generative framework is to specify hierarchical Bayesian models, where prior distributions reflect known constraints or typical ranges of physiological variables. In contrast, a discriminative model can still include domain knowledge through feature engineering or specialized architecture components (e.g., custom layers in neural networks). However, generative models can exploit domain knowledge more directly by encoding how data is produced, leading to improved interpretability of how each feature contributes to the final decision.
Can generative and discriminative models differ in how well they are calibrated?
Model calibration concerns how well the predicted probabilities align with true outcome frequencies. A well-calibrated classifier would output, for example, a probability of 0.7 for a label in such a way that among many samples receiving 0.7, about 70% truly belong to that class.
Generative models can suffer from calibration problems if their assumed P(X∣y) is not an accurate representation of the real distribution. The posterior P(y∣X) is then derived via Bayes’ rule, so if P(X∣y) or P(y) are poorly estimated, the resulting posterior can be systematically miscalibrated.
Discriminative models often aim directly to maximize the likelihood of P(y∣X) or minimize a loss function (like cross-entropy). This optimization can lead to good calibration, but it is not guaranteed. For instance, standard Logistic Regression without proper regularization can become overconfident on training data. Calibration can be improved by techniques like Platt scaling or isotonic regression. In many real-world scenarios, discriminative models may be relatively easier to calibrate because they focus on P(y∣X) directly, whereas generative models can become miscalibrated due to inaccuracies in P(X).
Are there scenarios in high-dimensional spaces where generative models outperform discriminative models?
High-dimensional data can pose challenges for both paradigms. Discriminative models can overfit if the number of parameters is large relative to the number of training samples. Generative models can also struggle if the assumed distribution cannot handle the complexity of high-dimensional feature dependencies. That said, there are certain high-dimensional settings (e.g., text classification) where Naive Bayes has famously done well, partly because the “naive” independence assumption can mitigate the curse of dimensionality by factorizing the joint distribution into simpler components.
An additional scenario is if the high-dimensional data has an underlying low-dimensional structure that is well-captured by a certain generative process (e.g., images generated by a manifold of latent variables). If that structure is explicitly modeled (like in a Variational Autoencoder), it can lead to powerful generative capabilities and sometimes yield competitive or superior classification performance in data-scarce conditions. However, for purely discriminative tasks in richly labeled, high-dimensional domains, methods such as deep neural networks (strongly discriminative) tend to dominate, provided enough data and computational resources are available.
What unique challenges arise when doing semi-supervised learning with generative versus discriminative models?
In semi-supervised learning, you have abundant unlabeled data but relatively few labels. A generative model naturally benefits from unlabeled data because it can refine its estimation of the overall data distribution P(X) even without labels. This refined P(X) can help produce more accurate class-conditional densities P(X∣y) or better approximate latent structures that then guide classification.
A purely discriminative model cannot directly learn from unlabeled data, since it focuses on P(y∣X). However, you can design semi-supervised discriminative techniques (e.g., consistency regularization, pseudo-labeling) that try to leverage unlabeled data by enforcing stable predictions. Still, these methods may be less straightforward than straightforwardly fitting P(X) in a generative paradigm.
A pitfall in semi-supervised generative modeling is if the unlabeled data distribution is substantially different from or only partially overlapping the distribution of the labeled data. The model might learn a misleading representation of P(X) that doesn’t help classification. Discriminative semi-supervised methods can also fail if the unlabeled data’s labeling distribution is drastically different from the labeled portion. Careful domain understanding and outlier detection can mitigate these risks.
Do generative models provide additional insights for interpretability compared to discriminative models?
Generative models attempt to capture how the data is generated. This can yield insights: for example, you can examine the learned parameters of P(X∣y) to see typical features or patterns for each class. In a Gaussian generative model, you can look at class-specific means and covariances to understand how features co-vary within each class. This interpretative advantage can be especially appealing in fields like biology, finance, or medicine, where understanding the underlying data distribution is important for trust and transparency.
Discriminative models can still be interpretable if they are simple (like Logistic Regression), but they do not provide a direct generative mechanism for how data might be produced. They focus on the boundary. More complex discriminative models (e.g., deep neural networks) typically have weaker interpretability, though explanation methods (like feature attributions) can help. Still, these methods may not offer as direct a story as an explicit P(X∣y) might.
What considerations arise in transfer learning settings for generative vs. discriminative approaches?
Transfer learning involves taking a model trained on one domain or task and adapting it to another domain or task. If you have a generative model that learns P(X), it might be easier to adapt to new tasks if the new tasks share a similar data distribution. You could keep much of the distributional knowledge intact and only adjust the conditional or the priors as needed for the new classes.
For a discriminative model, transfer learning often focuses on reusing learned features or embeddings from the source task. This is popular in computer vision or NLP, where pretrained classifiers or encoders can be fine-tuned for new tasks. However, if your discriminative model is specialized to a very specific boundary in the source domain, it may not generalize well to target domains that differ significantly.
A potential pitfall arises if your generative model incorrectly captures the source distribution in ways that do not generalize. Transfer might then require more extensive re-training. Similarly, a discriminative model with architecture-specific embeddings might not adapt well if the new domain has different modalities or drastically different feature distributions. The choice depends on how the source and target domains relate, and whether modeling P(X) or focusing on a decision boundary is more beneficial for the adaptation.
How do you handle imbalanced classes in generative vs. discriminative models?
Class imbalance occurs when one or more classes is underrepresented relative to others. In a generative framework, you model P(y) typically from the observed class frequencies, and if a minority class has very few examples, estimates of P(X∣y) for that class may be unreliable due to limited data. You could mitigate that by using stronger priors or additional domain knowledge to reduce variance in parameter estimates.
In a discriminative framework, class imbalance can cause the model to optimize in favor of the majority class. Logistic Regression may become biased toward predicting the majority class if you do not adjust the loss function or apply class weights. A standard approach is to weight the loss function more heavily for the minority class, or to sample the training data to rebalance it (oversampling minority classes, undersampling majority classes, or using synthetic data methods like SMOTE).
Are there ways to leverage deep learning architectures for generative vs. discriminative tasks, and how does that compare to classical models?
Modern deep learning provides architectures specifically for generative modeling (e.g., Variational Autoencoders, Generative Adversarial Networks, Normalizing Flows). These methods can learn to generate complex, high-dimensional data (images, audio, text) in ways that classical generative models like Naive Bayes cannot match. If your goal is not just classification but also synthetic data creation, or if you want a better internal representation of P(X), these neural-based generative models are highly relevant.
On the discriminative side, deep neural networks (e.g., convolutional or transformer-based) have become the standard for classification tasks in computer vision, NLP, and other domains. They often require large labeled datasets and significant computational resources. They do not directly model P(X) but can achieve state-of-the-art classification accuracy.
A potential pitfall in applying deep generative models is that they can be harder to train, requiring careful hyperparameter tuning, large datasets, and specialized architectures. They can also be prone to mode collapse (in GANs) or difficulties with optimization. Deep discriminative models can similarly be prone to overfitting if there’s insufficient data or poor regularization. The choice may depend on whether you need generative capabilities or only classification performance.
How would you test whether a given generative model accurately captures the real data distribution?
Evaluating a generative model is often more subtle than evaluating a discriminative one, because for classification tasks, you can measure accuracy, precision, recall, etc. For generative models, you want to see how well P(X) is approximated. Possible strategies include:
Log-likelihood estimation: If tractable, compute the model’s log-likelihood on held-out data. Higher likelihood indicates a better fit, although models can sometimes “memorize” training data in high-dimensional spaces.
Sample quality inspection: Generate synthetic samples from the model and visually or statistically inspect them. This can be subjective, though some metrics (like the Frechet Inception Distance in image generation tasks) attempt to provide objective scoring.
Reconstruction fidelity: In models that allow reconstruction (like VAEs), compare how well the generative model reconstructs unseen data. Good reconstructions suggest the latent representation captured key data features, though it might not guarantee coverage of all modes.
Statistical tests: Use tests like the Kolmogorov–Smirnov test or compare summary statistics if a particular distribution shape is expected. Pitfalls arise if you only test certain marginals or fail to capture correlations across features.
These methods focus on ensuring the generative model’s representation is realistic. Even if a model scores well on these metrics, that does not always ensure optimal classification performance. It is possible for a model to do well in generating realistic samples but not necessarily be the best at discriminating among classes.