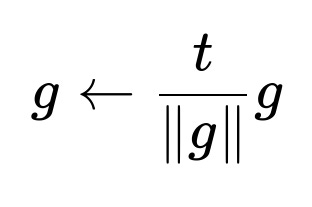ML Interview Q Series: Gradient Clipping for Mitigating Exploding Gradients in Deep Networks

📚 Browse the full ML Interview series here.

Gradient Clipping: What is gradient clipping and when would you use it? Provide an example scenario, such as training an RNN or deep network where gradients might explode, and explain how clipping the gradients (by value or norm) helps stabilize training.

Gradient clipping is a technique that constrains or “clips” the magnitude of gradients during backpropagation to prevent excessively large parameter updates. In deep neural networks, especially recurrent architectures or very deep feedforward ones, gradients can sometimes accumulate to extremely large values (a phenomenon commonly called the “exploding gradient problem”). Such large gradients can destabilize training, cause numerical overflows, or lead to very erratic parameter updates.

Below is a detailed explanation of how gradient clipping works, why we do it, and how it is typically applied.

Deep architectures, such as RNNs or LSTMs, can suffer from exploding gradients because repeated multiplication of gradients through time (or depth) can amplify values beyond manageable scales. By constraining the gradient magnitude, we can avoid updates that are too large and ensure more stable convergence.

Clipping can be done in two main ways:

• Clipping by value

• Clipping by norm

Clipping by value places a direct bound on each component of the gradient tensor. Clipping by norm rescales the entire gradient vector when its overall norm exceeds a threshold. Both approaches stabilize training by ensuring that the gradient vector does not exceed certain limits.

Heading and Sub-heading Explanation

Understanding Exploding Gradients in RNNs or Deep Networks

Long sequences or deep networks often involve many repetitive multiplication steps when unrolling through time or depth. Each parameter update depends on gradients that can grow large whenever certain patterns of weight matrices have eigenvalues greater than 1 or if the scale of the input and internal weights compound the gradient. Over multiple layers or timesteps, a small initial gradient can grow exponentially. This instability can manifest as extreme weight updates, causing the loss function to fluctuate wildly, potentially leading to divergence rather than convergence.

Mathematical Description of Gradient Norm Clipping

When clipping by norm, we often choose a threshold tt. We compute the norm of the gradient vector g, and if ∥g∥>t, we rescale:

This means if the total norm exceeds t, we shrink g so that its new norm is exactly t. This is preferred in many situations because it preserves the direction of g but limits its magnitude. For smaller norms (below the threshold), the gradient remains unchanged. This avoids outliers in the update step.

When to Use Gradient Clipping

We typically use gradient clipping in scenarios where:

• We observe “NaN” losses in training, possibly due to overflow.

• Large training instabilities or high variance in parameter updates.

• Models with recurrent connections or deep layers where the gradient must flow through many transformations.

Examples might include language modeling with RNNs or LSTMs over long text sequences, training Transformers on large datasets, or training generative models with extremely deep architectures.

How Clipping Helps Stabilize Training

By bounding the gradient magnitude, we reduce the risk that a single parameter update will “overshoot,” causing training to diverge. This is especially valuable early in training, when weights are randomly initialized, or in regions of the parameter space where gradients can blow up. Clipping effectively guards against outliers in gradient magnitude while preserving the overall direction of the updates.

Subtlety: Choosing the Clipping Threshold

If the threshold is too low, gradients become very small, and training might stall or converge too slowly. If it is too high, clipping rarely happens, diminishing its practical effect. Consequently, one typically sets the threshold by empirical experimentation—perhaps starting with moderate values (like 1.0, 5.0, or 10.0 in norm clipping, depending on the scale of loss gradients) and monitoring training stability.

Implementation Example in PyTorch

One common approach in frameworks like PyTorch:

import torch
import torch.nn as nn
import torch.optim as optim

# Suppose we have a model:
model = nn.LSTM(input_size=10, hidden_size=20, num_layers=2)
optimizer = optim.Adam(model.parameters(), lr=0.001)

# A simple training loop snippet:
for batch_idx, (inputs, targets) in enumerate(training_data_loader):
    optimizer.zero_grad()

    # Forward pass:
    outputs, hidden_state = model(inputs)
    loss = loss_function(outputs, targets)

    # Backprop:
    loss.backward()

    # Gradient clipping by norm:
    torch.nn.utils.clip_grad_norm_(model.parameters(), max_norm=5.0)

    optimizer.step()

Here, clip_grad_norm_ rescales the gradients in model.parameters() if their collective norm exceeds max_norm=5.0. This is a typical approach for RNN or LSTM training where exploding gradients often occur.

Value-Based Clipping

Value-based clipping sets each gradient component within a specified range. For example, we can clip every component of the gradient to lie between −v and +v. In PyTorch, it can look like:

torch.nn.utils.clip_grad_value_(model.parameters(), clip_value=0.5)

This ensures no single component of the gradient exceeds 0.5 or goes below -0.5. This approach might slightly distort the overall gradient direction if only some components are large. Nonetheless, it is straightforward and sometimes effective for controlling outlier components.

Practical Example Scenario: Training an RNN Language Model

Consider training a language model on a large corpus where the RNN processes sequences of up to 200 tokens. At each time step, the gradient backpropagates through the entire unrolled sequence. This can easily cause gradient values to explode if the network weights amplify the gradient. By applying gradient clipping (either by norm or value), you prevent any single update from becoming astronomically large, maintaining a more stable training trajectory.

Why This Stabilizes Training

Exploding gradients can make the loss function fluctuate between very high and very low values. That often leads to numerical instability (loss = NaN), or the optimizer skipping over minima. Clipping effectively bounds these fluctuations and ensures each update is more consistent.

Advantages and Possible Concerns

• Advantages:

  • Stabilizes training.

  • Avoids numerical overflow.

  • Particularly helpful in deep or recurrent architectures.

• Concerns:

  • A poorly chosen threshold might hamper convergence if set too low.

  • If you never see the clipping “activate,” your threshold might be too large.

Below are some possible follow-up questions that FANG interviewers may ask, along with thorough answers.

Could you describe the difference between norm-based clipping and value-based clipping in detail?

Norm-based clipping rescales the entire gradient vector if its norm exceeds a certain threshold. This keeps the direction intact while limiting the magnitude. It compares the overall gradient size to a threshold. Specifically, one calculates:

A practical consideration is that norm-based clipping behaves more gracefully if most gradient components are of a reasonable scale, but there is a single large direction pushing the norm over the threshold. In that situation, norm-based clipping preserves the direction. Value-based clipping can more drastically alter the gradient by truncating each component individually.

When might gradient clipping not solve your training instability issues?

Clipping can address the symptom of exploding gradients, but not always the root cause. If there is a deeper architectural or data issue—for example, if your model is unbounded or your learning rate is extremely high—clipping alone might not be sufficient. Specifically:

• If the model’s initialization is poor, the gradients might frequently explode even with clipping, slowing training significantly.

• If the learning rate is too large, even clipped gradients can push updates too aggressively and cause oscillations.

• If the sequence length or network depth is extremely large and the model design does not incorporate gating or residual connections, you might need architecture changes (e.g., LSTM/GRU/Transformers) to mitigate the exploding or vanishing gradients.

In these cases, gradient clipping is a safeguard, but you often need to combine it with well-chosen hyperparameters, careful initialization, and suitable architecture design.

Are there any performance trade-offs when using gradient clipping?

While gradient clipping helps training stability, it can slow convergence if clipping occurs too frequently at too low a threshold. This can cause many updates to be smaller than they would be otherwise. The net effect is typically positive for challenging tasks prone to exploding gradients, but a suboptimal clipping threshold could limit the rate of learning.

In practice, the performance overhead of computing the gradient norm and applying clipping is typically minor compared to the total cost of forward/backward passes. It is more of an issue regarding how quickly your model reaches good performance. So the main trade-off is between stability and the risk of limiting beneficial gradient magnitudes.

Could you show how to implement gradient clipping in TensorFlow?

Below is an example snippet using TensorFlow 2.x with the Keras API. We can manually clip gradients within a custom training loop:

import tensorflow as tf

model = tf.keras.Sequential([
    tf.keras.layers.LSTM(20, input_shape=(None, 10)),  # Example shape
    tf.keras.layers.Dense(1)
])

loss_fn = tf.keras.losses.MeanSquaredError()
optimizer = tf.keras.optimizers.Adam()

@tf.function
def train_step(x, y):
    with tf.GradientTape() as tape:
        predictions = model(x, training=True)
        loss_value = loss_fn(y, predictions)

    grads = tape.gradient(loss_value, model.trainable_variables)

    # Clip by norm:
    clipped_grads = [tf.clip_by_norm(g, 5.0) for g in grads]

    # Or, clip by value:
    # clipped_grads = [tf.clip_by_value(g, -0.5, 0.5) for g in grads]

    optimizer.apply_gradients(zip(clipped_grads, model.trainable_variables))
    return loss_value

# Example usage:
for epoch in range(10):
    for x_batch, y_batch in dataset:
        loss = train_step(x_batch, y_batch)

In this example, we used tf.clip_by_norm() to rescale gradients whose norm exceeds 5.0. This matches the concept of norm-based clipping in PyTorch. Alternatively, we could use value-based clipping by calling tf.clip_by_value().

Could you elaborate on best practices and thresholds for gradient clipping?

Choosing threshold values is mostly empirical. Some common guidelines:

• For norm clipping, a threshold in the range of 1.0 to 10.0 is common in many RNN or LSTM tasks.

• One might track how often clipping occurs. If it happens at every step, your threshold might be too low. If it rarely occurs, your threshold might be too high.

• Use a validation set or monitored training curves to see if your model is diverging or if the updates are too small. Adjust thresholds accordingly.

Other best practices include:

• Carefully choosing an appropriate learning rate schedule to reduce the chance of exploding gradients.

• Incorporating architectural elements like residual connections, gating mechanisms (in LSTMs/GRUs), or normalization layers to mitigate gradient explosion or vanishing.

• Checking for data anomalies that might lead to large losses or inputs that blow up the hidden states.

When combined with these strategies, gradient clipping becomes a powerful tool to ensure stable and effective training of deep or recurrent networks.

---

Below are additional follow-up questions

How does gradient clipping interact with momentum-based optimizers like SGD with momentum or Adam?

When using momentum-based methods such as SGD with momentum or Adam, the parameter update is influenced by both the current gradient and accumulated past gradients. If we clip the current gradient, this affects the instantaneous contribution to the momentum term but does not directly reset or eliminate momentum that was accumulated in previous steps.

For instance, in SGD with momentum, the velocity vector (which accumulates past gradients) might still contain large values even if the current gradient is clipped. This can lead to larger updates than anticipated if the accumulated velocity is substantial. Consequently, if exploding gradients are partially caused by large velocities, we need to monitor whether momentum is also becoming excessive.

One subtle point is that clipping can significantly alter the effective gradient direction when combined with momentum. If you always clip large gradients, you might prevent the velocity from capturing the true direction of steepest descent. Instead, the momentum can accumulate in directions that repeatedly get clipped, leading to somewhat erratic or slower convergence.

A potential pitfall is ignoring the effect of momentum when diagnosing why a model is diverging. For instance, you might see that individual step gradients have reasonable magnitudes (thanks to clipping), yet the combined update is still large. This is often because the momentum buffer itself got large prior to clipping or because the effective learning rate (especially in adaptive methods like Adam) was too high.

In edge cases, one might combine gradient clipping with “velocity damping” (manually scaling down momentum buffers when they exceed certain thresholds) to fully control updates. However, this is less common, and typically carefully tuning momentum hyperparameters (e.g., beta values in Adam or momentum coefficient in SGD) plus clipping is sufficient in most real-world scenarios.

How do you decide whether to clip gradients in a single layer versus the entire network?

Gradient clipping can be applied globally (across all parameters in the network) or locally (on a per-layer or per-parameter-group basis). The most common approach is global clipping, where one computes the norm of all parameter gradients in the model, then rescales them as needed. However, there might be scenarios where you prefer a more fine-grained approach:

• Local (per-layer) clipping: You compute the gradient norm for each layer’s parameters separately, then clip each layer’s gradients if they exceed a certain threshold. This can be useful if some layers systematically produce larger gradients than others. For example, an embedding layer might produce extremely large gradients due to certain tokens or outliers in language modeling, while other parts of the network have stable gradients. By clipping only the problematic layer, you avoid over-constraining the rest of the network.

• Global clipping: This is usually simpler and standard. You treat the network’s parameters as one combined vector and rescale all parameters together when the global norm exceeds the threshold. This helps maintain the correct ratio of gradient magnitudes between different layers.

A potential pitfall with local clipping is that you might inadvertently “under-update” certain layers that consistently exceed the threshold while letting other layers update more freely. This imbalance could lead to slower or suboptimal training. On the other hand, if one layer has stable gradients and another has extremely large gradients, global clipping might disproportionately shrink updates in the stable layers simply because the large-gradient layer pushes the overall norm above the threshold.

In practice, global clipping is most frequently used, and local clipping is a specialized technique reserved for architectures where one or two layers are known to produce unstable gradients.

What are common signs that gradient clipping should be used (or is insufficient) in large-scale distributed training?

In large-scale distributed setups, gradients are typically aggregated (summed or averaged) across multiple GPUs or machines. This scenario can exacerbate exploding gradients because:

• When multiple workers compute gradients on different mini-batches and aggregate them, outlier gradients from any single worker could blow up the entire sum.

• The overall effective batch size might be huge, amplifying even moderate gradient components.

Signs that clipping might be necessary:

• Frequent NaNs in the loss across different workers or ranks.

• Instability in the training curve, with repeated spikes in the loss.

• Very large updates or large parameter changes between checkpoints.

However, if clipping alone does not resolve instability in distributed training, other issues may be at play:

• Learning rate might be too high: When using large batch sizes in distributed setups, you might have scaled the learning rate incorrectly (often you might linearly scale the learning rate with batch size, but that can cause instability at very large scales).

• Synchronization anomalies: If the gradient aggregation step is misconfigured or if there is partial data corruption, the system might produce wildly incorrect gradients that no amount of clipping can fix.

• Data skew: If different workers see highly varied data distributions, certain gradients might be consistently larger or smaller, resulting in sporadic large updates.

In such cases, combining gradient clipping with carefully tuned learning rates, correct data shuffling, or advanced distributed optimizers is crucial. Additionally, thorough logging on each worker can help detect which rank is producing the outlier gradients and if clipping is happening too frequently in that worker.

How does gradient clipping relate to gradient penalty techniques often used in GANs or adversarial training?

In certain adversarial training or GAN-related tasks, researchers sometimes use a “gradient penalty” term that explicitly penalizes large gradients in the loss function. For example, in WGAN-GP (Wasserstein GAN with Gradient Penalty), there is a regularization term that encourages gradients of the discriminator with respect to the inputs to have a norm close to 1. This is conceptually different from gradient clipping, which restricts the magnitude of parameter gradients to control updates rather than shaping the gradient field around input samples.

While both approaches restrict large gradients, they do so in different ways:

• Gradient clipping directly modifies the backpropagated gradients with respect to parameters to avoid big parameter updates.

• Gradient penalty modifies the training objective by adding a term that penalizes large gradients with respect to the model’s input or intermediate activations. This influences how the model learns to map inputs to outputs, rather than directly limiting the size of the parameter update.

A subtle pitfall is to conflate gradient clipping with gradient penalty. Even if you use a gradient penalty in a GAN, you might still need gradient clipping on your generator or discriminator if they suffer from exploding updates. Conversely, gradient clipping does not enforce any constraint on how the model’s activations or outputs vary with respect to the input; it only constrains parameter updates.

Is gradient clipping relevant in second-order or quasi-Newton optimizers?

In second-order methods (like full Newton’s method or quasi-Newton methods such as L-BFGS), the parameter update typically involves an approximate Hessian or Hessian-vector product. These methods generally compute a search direction that can also become very large, especially if the approximate Hessian indicates a steep direction.

Although second-order methods are less commonly used in large-scale deep learning (due to computational overhead), explosive parameter updates can still occur. In principle, gradient clipping can be applied to the first-order gradient prior to forming or updating the Hessian approximation. Alternatively, one might apply clipping to the final search direction if it becomes too large. However, with second-order methods, other forms of damping or line search are more common ways to avoid steps that are too big.

A potential edge case is that if you blindly clip the raw gradient used in second-order updates, you might disrupt the Hessian approximation’s integrity. This could degrade the benefits of the second-order method. If second-order updates are consistently exploding, you might want to lower the effective learning rate or add more robust damping/regularization in the Hessian approximation.

What if we apply gradient clipping after applying some custom gradient transformation?

Sometimes in advanced architectures or training regimes, you might transform gradients for specific parts of the network (e.g., using custom backward passes or dynamic computational graphs that manipulate gradients). If you clip gradients before this transformation, it might not address the real cause of large updates. Conversely, if you do it after the transformation, you risk ignoring the magnitude of the raw gradient that flows through the rest of the network.

For instance, in some reinforcement learning algorithms, one might do gradient scaling or advantage normalization before or after combining policy and value function gradients. The question is: should clipping be done on the raw policy gradient, or on the combined gradient after weighting, or on the final gradient that goes into the optimizer?

A subtle pitfall is that if your custom transformation amplifies small gradients or specifically zeroes out certain components, you can get unanticipated side effects. For example, if you zero out certain gradient components and then perform global norm clipping, the final norm might differ significantly from your expectation. The recommended practice is to identify the place in the pipeline where the gradient best represents your final update direction, and then apply clipping at that point.

How do we handle gradient clipping when using gradient accumulation for very large batch training?

In some scenarios (e.g., limited GPU memory), you may accumulate gradients over multiple forward-backward passes (micro-batches) before doing an optimizer step. The question is whether to apply clipping after each micro-batch or only once after all gradients are accumulated for the effective batch.

• Clip after each micro-batch: This might be safer if you suspect that partial gradients can explode. However, repeatedly clipping might introduce distortions, since each micro-batch’s gradient direction is being clipped before being added to the total.

• Clip once after accumulating: This approach calculates the gradient for the entire effective batch, then applies a single clip. It is more faithful to the concept of gradient clipping relative to the entire batch. If the total gradient from the combined micro-batches is extremely large, it will get clipped.

A potential issue arises if you do not clip intermediate micro-batch gradients in a scenario where they can overflow the floating-point range (e.g., FP16 training with a large dynamic range). In that case, even though the final combined gradient might be clipped, you might already have introduced numerical NaNs. A practical solution is to do partial clipping or gradient scaling in mixed-precision setups, or to ensure that the dynamic loss scaling mechanism in frameworks like PyTorch AMP or TensorFlow mixed precision is robust enough to avoid overflows.

Is there a risk that gradient clipping masks deeper architectural or hyperparameter issues?

Yes. Gradient clipping can sometimes be used as a “band-aid” to hide more fundamental problems:

• Poor weight initialization: If weights are poorly initialized (e.g., extremely large or small), you might see exploding or vanishing gradients. Clipping keeps the magnitudes in check, but the training might still be suboptimal.

• Inappropriate activation functions: Using activation functions that lead to unbounded outputs (e.g., certain custom variants of ReLU or exponentials without constraint) can cause large intermediate values that might blow up the gradient. Clipping will control the updates, but you could suffer from a model architecture that is prone to numeric instability.

• Incorrect scaling of input data: If the input features aren’t normalized or scaled, large inputs can cause large gradient magnitudes. Clipping will mitigate the symptom (exploding updates) but not fix the root cause (data not normalized properly).

In each of these scenarios, the model may be training sub-optimally, and gradient clipping only prevents catastrophic failure rather than resolving the reason the gradients became huge in the first place. While clipping is a standard practice, especially for recurrent models, it should be used alongside robust architecture design, hyperparameter tuning, proper initialization, and data normalization to achieve the best performance.