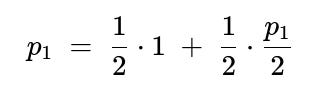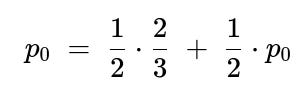ML Interview Q Series: HHT vs HTT First Occurrence Probability: A Markov Chain Analysis
Browse all the Probability Interview Questions here.
Suppose you keep flipping a fair coin until you first observe either Heads-Heads-Tails or Heads-Tails-Tails. Which pattern is more likely to occur initially and what is that probability?
Comprehensive Explanation
A valuable way to approach this problem is by considering it as a Markov chain or state-based system that tracks partial progress toward either sequence (HHT or HTT). Because the coin is fair, each flip has probability 1/2 for Heads (H) and 1/2 for Tails (T). The essential question is: starting from scratch, how do we figure out the probability that the pattern HHT appears before the pattern HTT?
State Definitions
We can define a few distinct states based on how much of each target sequence we have currently matched.
S0: No progress has been made (starting state).
S1: We have just observed
H.S2: We have just observed
HH.S3: We have just observed
HT.HHT: We have observed HHT (pattern found).
HTT: We have observed HTT (pattern found).
Once we reach either HHT or HTT, the process terminates.
Transition Logic
From each state, the next coin flip takes us to a new state:
• S0
If we flip H, move to S1.
If we flip T, stay in S0 (because a lone T does not help match HHT or HTT yet).
• S1 (we have "H")
If we flip H, move to S2 (sequence is now "HH").
If we flip T, move to S3 (sequence is now "HT").
• S2 (we have "HH")
If we flip H, we remain in S2 (the last two flips are still "HH").
If we flip T, we arrive at HHT (the sequence "HHT" is completed).
• S3 (we have "HT")
If we flip T, we arrive at HTT (the sequence "HTT" is completed).
If we flip H, we move to S1 (the new last flip is "H", so partial pattern is just "H").
Probability Computation
Let p0 be the probability that we eventually see HHT before HTT starting from state S0. Similarly define p1, p2, and p3 for states S1, S2, and S3.
We know:
• From S2:
The next T leads directly to HHT, so that event occurs with probability 1/2.
The next H keeps us in S2 with probability 1/2. Eventually, a T will come up in S2, guaranteeing HHT. Therefore p2 = 1 (once you reach S2, you are certain to see HHT first).
• From S3:
The next T leads directly to HTT, so in that branch the probability of getting HHT first is 0.
The next H leads to S1, so we add 1/2 * p1. Hence p3 = (1/2)*0 + (1/2)*p1 = p1/2.
• From S1:
With probability 1/2 we flip H, move to S2 (where p2=1).
With probability 1/2 we flip T, move to S3 (where p3 = p1/2).
We can write that in a single equation:
Solving for p1:
p1 = 1/2 + (1/4)p1 (3/4)p1 = 1/2 p1 = 2/3
Once we have p1, we see that p3 = p1/2 = 1/3.
Finally, from S0:
With probability 1/2 we move to S1 (p1=2/3).
With probability 1/2 we stay in S0 (which again has probability p0 of leading to HHT).
Let p0 be the probability from S0:
Solve for p0:
(1/2)p0 = 1/3 p0 = 2/3
Hence, from the start (S0), the probability of encountering HHT first is 2/3. Consequently, the probability of encountering HTT first is 1 - 2/3 = 1/3.
The final answer is that HHT is more likely to occur first, and it does so with probability 2/3, while HTT appears first with probability 1/3.
Demonstration with Python
Below is a short code snippet that can demonstrate this result via simulation. It runs a large number of trials where we flip a fair coin until HHT or HTT appears, then records which pattern comes first.
import random
def simulate(num_trials=10_000_00):
count_hht_first = 0
for _ in range(num_trials):
flips = []
while True:
flips.append(random.choice(['H','T']))
# Check for HHT
if len(flips) >= 3 and flips[-3:] == ['H','H','T']:
count_hht_first += 1
break
# Check for HTT
if len(flips) >= 3 and flips[-3:] == ['H','T','T']:
break
return count_hht_first / num_trials
prob_hht = simulate()
print("Estimated Probability of HHT appearing first:", prob_hht)
Running this simulation repeatedly should yield a value close to 0.6667 (2/3).
Why HHT Has the Advantage
The key reason HHT is more likely to appear first has to do with the overlapping structure of the sequences. Specifically, once you get "HH", you are essentially locked into eventually getting HHT because only one T is needed, and any additional H flips keep you in the "HH" state. On the other hand, if you see "HT" and then get an H, you do not jump to a near-complete pattern but instead revert to a simpler partial match (just "H").
Potential Follow-up Questions
Why is there no possibility of "losing progress" once you reach HH?
If you are in a state that has "HH" and you see another H, the last two flips are still "HH" so you remain in the same partial-match state. This means you never truly reset to a no-match state. In contrast, if you have "HT" and see another H, you partially regress to having only a single "H." So from "HH," you are effectively stuck in a loop that will inevitably see a T and complete HHT.
How would the result change if the coin were biased?
If the coin probability of heads is p and tails is (1-p), the same Markov chain approach works. However, the transition probabilities change accordingly. Each step in the state machine is no longer 1/2 but depends on p. One would set up the same equations but replace each 1/2 with either p or (1-p) as appropriate. The resulting linear equations would yield a different probability for HHT or HTT. In general, the approach remains the same: define states and transition probabilities, then solve for the probability of finishing in HHT before HTT.
Could a simpler combinatorial argument be used?
One might attempt a combinatorial approach, but because of overlapping sequences and infinite potential flips, direct combinatorial counting is tricky. The Markov chain or state-based method is the most systematic and clearer solution. Alternatively, advanced methods like using Penney’s game style analyses or considering the expected times can also be done, but they typically reduce to a similar reasoning about partial matches and transitions.
How does partial overlap create differences in these string-appearance problems?
Partial overlap means that a string’s suffix can serve as a prefix of the target string. For instance, in "HHT," the overlapping suffix "H" can appear in different ways depending on the next flip. These overlaps create an asymmetric dynamic: some patterns are more “stable” under repeated flips, making them more likely to appear before others, even if the coin is fair.
Edge Cases and Practical Tips
While HHT and HTT are short sequences, for longer sequences the same fundamental approach still applies. One must carefully account for overlapping subsequences.
Implementation detail in code: It’s essential to always check for the newly formed 3-flip pattern at the end of the flips list, as soon as it reaches length 3 or more.
If the coin flips were not i.i.d. (e.g., some memory effect or Markovian correlation), the entire approach changes. The independence assumption is crucial for straightforward analysis.
These considerations help ensure you fully grasp why HHT emerges with higher probability than HTT, even with a fair coin.
Below are additional follow-up questions
What if the sequences were longer, for example HHTT versus HTTT? How would you approach such a scenario?
One can generalize the same state-based Markov chain method or partial overlap approach to longer sequences. The procedure is as follows:
• Identify all partial matches relevant to each target sequence, such that these partial matches track your current state in approaching a final pattern. • Construct a finite-state machine that captures each “progress state” for each of the two sequences. This will include every unique prefix condition (like H, HH, HHT, etc.) that could lead to either final sequence. • Determine the transitions from one state to another for each possible coin outcome (Heads or Tails). • Solve a system of linear equations that represent the probability of eventually reaching one pattern over the other from each state.
Pitfalls or edge cases:
• Overlapping patterns can be more complex to analyze (e.g., a sequence might overlap with itself). If the same substring can serve as the starting point for multiple patterns, the state transition logic must carefully keep track of which new partial sequences become relevant. • For very long sequences, enumerating all possible states can become cumbersome. In such cases, one might need more optimized dynamic programming or advanced string processing (like the Knuth-Morris-Pratt failure function) to handle overlaps systematically.
How do you calculate the expected number of coin flips required before one of the patterns appears?
To compute the expected time to absorption (i.e., the expected number of flips before either pattern occurs), you expand the Markov chain approach to include the notion of expected time in each state. For each state S, define E(S) as the expected number of flips before absorption starting from that state. Then the equations follow this logic:
• E(S) = 1 + (p * E(S') + q * E(S''))
where p, q are transition probabilities to next states S' and S'' depending on the coin outcome, and the “+1” accounts for the flip you just made. For an absorbing state (i.e., HHT or HTT), the expected time from that state is 0. After setting up these equations, solve them to find the expected number of flips starting from the initial state.
Pitfalls or edge cases:
• If the sequences share long overlaps, you can get non-trivial cycles that inflate the expected number of flips. • It is easy to make an off-by-one mistake when you incorporate the additional flip for each transition. Carefully write down each term and confirm the logic for adding 1.
Would the result change if we did not stop after one pattern is found but continued flipping until both patterns have appeared at least once?
In this extended scenario, the analysis splits into two phases:
• Phase 1: Wait for the first occurrence of either HHT or HTT. • Phase 2: Starting from the moment one of them appears, continue until the second pattern eventually appears.
For Phase 1, the probability and expected time to see HHT or HTT first remain the same (2/3 for HHT first, 1/3 for HTT first). Once you know which appeared first, the probability and expected time to see the other pattern might involve new states, depending on how much overlap can exist between the patterns. In practice, you would:
• Identify the partial state implied by the moment you saw the first pattern. • Re-run a state-based approach to find the probability and expected time to see the second pattern from this new state.
Pitfalls or edge cases:
• The pattern that was found first might partially fulfill the second pattern (e.g., the last few coin flips that ended the first pattern might also form a partial prefix of the second pattern). • If the two patterns share a large overlap (say, HHTT and HTTT share an overlap of T at the end or something more complex in a bigger scenario), that changes your initial state for Phase 2.
Could a correlation in coin flips (a coin that is not memoryless) alter the analysis significantly?
Yes. The entire approach assumes independent and identically distributed (i.i.d.) flips. If flips are correlated, standard Markov chain analysis for a memoryless process no longer directly applies. For a coin that has memory or correlation:
• You would need a higher-order Markov model that tracks additional “history” beyond just the current partial match states. Specifically, you might track not just your partial alignment with HHT or HTT but also the state of the coin’s internal correlation mechanism. • If the correlation is moderate, you might approximate independence, but an exact solution would become more complex and typically require domain-specific knowledge about how the coin’s bias evolves over time.
Pitfalls or edge cases:
• Even small correlation can distort probabilities over many flips if the correlation is systematic. • Overlapping sequences can magnify the effects of correlation, because the correlation might systematically cause runs of Heads or Tails that favor one pattern.
Can we use a direct recursive approach without explicitly naming Markov chain states?
Yes, one might try a direct recursion on the probability of eventually seeing HHT before HTT, based on the outcomes of the next coin flip(s). For instance, let p be the probability that HHT occurs before HTT from the start:
p = 1/2 * [ probability if we flip H first ] + 1/2 * [ probability if we flip T first ]
Then you recursively expand the “probability if we flip H first,” which might itself be built from smaller events. Ultimately, the underlying structure is still that of a Markov chain, but you’re expressing it in a purely recursive format.
Pitfalls or edge cases:
• It is easy to double-count or miss states if you do not methodically track partial matches. • You might find yourself re-deriving the same states informally. This approach can be prone to “logical loops” if you do not handle overlapping sequences correctly.
Could an adversarial arrangement of outcomes affect which pattern appears first?
If an adversary had the power to choose the flips (not random, but adversarial), they could obviously force any pattern to appear first. That scenario is no longer a probabilistic question; it is more of a game-theoretic or combinatorial puzzle:
• An adversary can design a sequence of H/T to postpone or accelerate certain patterns. For example, if the adversary wants to avoid HHT indefinitely, they might inject T flips to break any partial HH progress. • By controlling each flip outcome, the adversary can sequence the flips to produce HTT or HHT at whichever time they desire, or possibly cycle states to never let certain patterns appear.
Pitfalls or edge cases:
• If you impose constraints on how “adversarial” the flips can be (for instance, not fully adversarial but limited in power), the solution might become a new type of constrained random process. • In real-world coin flips, you rarely have an adversary controlling the outcome, but it is still a fun hypothetical to illustrate how these patterns rely crucially on randomness.
What happens if the coin is no longer discrete, for example if we generalize to a system of random “symbols” with more than two possible outcomes?
In principle, you can extend the entire approach to an alphabet of size k > 2. For instance, if each “flip” can land in one of three states (A, B, C) with probabilities pA, pB, pC, and you watch for particular sequences of length n. The approach still relies on:
• Defining states representing how much of the pattern has been matched so far. • Transitioning among these states based on which symbol you observe next. • Stopping when you match any of the “target” sequences.
Pitfalls or edge cases:
• The state space might grow significantly for bigger alphabets or longer patterns. • Overlaps become more complicated to handle intuitively, though the same principle remains the same.