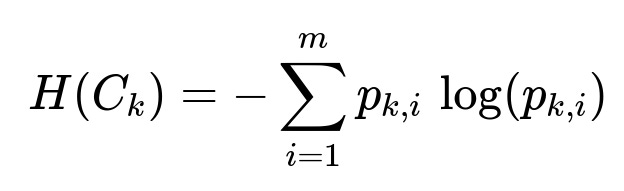ML Interview Q Series: How can entropy serve as a criterion for assessing the quality of clusters?
📚 Browse the full ML Interview series here.
Comprehensive Explanation
Entropy, in the context of clustering validation, is typically used to gauge how well a set of clusters corresponds to existing ground-truth class labels. When applied as an external cluster validation measure, it shows whether each cluster is predominantly composed of points belonging to a single class or whether it contains a more diverse mixture of classes. Lower entropy indicates higher homogeneity (the cluster mostly contains points from a single class), whereas higher entropy suggests greater impurity (the cluster contains points from multiple classes in roughly similar proportions).
When evaluating a clustering solution, the usual approach is to calculate the entropy of each cluster based on the distribution of ground-truth classes within that cluster, and then combine those entropy values into a single metric over all clusters. Entropy can thus provide a direct reflection of how effectively the clustering process has separated data points that share the same class label.
Mathematical Formulation
To compute the entropy of a particular cluster C_k, one typically considers how that cluster’s points are distributed across the possible class labels. If there are m distinct classes in the dataset and p_{k,i} represents the fraction of points in cluster C_k that belong to class i, then the entropy for cluster C_k can be written as:
Here, p_{k,i} is an inline textual notation denoting the ratio n_{k,i}/n_k, where n_{k,i} is the count of points in cluster C_k that belong to class i, and n_k is the total number of points in cluster C_k. The base of the logarithm can be 2 or e, depending on whether one wants the measure in bits or in nats, but the overall interpretation remains the same: smaller values correspond to more homogeneous clusters.
The global entropy H of the entire clustering solution is typically calculated as a weighted sum of these cluster entropies, where each cluster’s contribution is weighted by its relative size n_k out of the total number of points N in the dataset:
In this expression, K is the total number of clusters, n_k is the number of data points in cluster C_k, N is the total number of data points across all clusters, and H(C_k) is the entropy for cluster C_k given by the first formula. This final quantity H indicates the average impurity across the entire clustering solution. A lower value of H means that on average, each cluster is more homogeneous (and hence better matches the ground-truth class labeling).
Practical Considerations
One potential drawback is that if a dataset contains many small clusters, each could appear to have low entropy if it only happens to contain a handful of points from the same class. This can inflate the impression of purity. It is therefore important to consider the distribution of cluster sizes when interpreting the overall entropy score.
Another consideration is that entropy compares the clustering outcome to existing class labels. If no labels are available, entropy cannot be computed in this standard manner, because the measure intrinsically relies on how well discovered clusters align with known classes.
Example Python Snippet
Below is a brief example using Python to illustrate how one might compute overall entropy for an externally labeled dataset and a chosen clustering result. This snippet assumes you already have two arrays: cluster_assignments, which has a cluster index for each data point, and true_labels, which has the ground-truth class label for each data point.
import numpy as np
import math
def cluster_entropy(cluster_assignments, true_labels):
unique_clusters = np.unique(cluster_assignments)
total_points = len(cluster_assignments)
overall_entropy = 0.0
for c in unique_clusters:
indices = np.where(cluster_assignments == c)[0]
cluster_size = len(indices)
# Count how many points in this cluster belong to each class
label_counts = {}
for idx in indices:
label = true_labels[idx]
label_counts[label] = label_counts.get(label, 0) + 1
# Calculate the cluster's entropy
cluster_entropy_val = 0.0
for label, count in label_counts.items():
p = count / cluster_size
cluster_entropy_val -= p * math.log(p, 2) # log base 2
# Weight by cluster's size
overall_entropy += (cluster_size / total_points) * cluster_entropy_val
return overall_entropy
# Example usage
cluster_assignments = np.array([0, 0, 1, 1, 1, 2, 2])
true_labels = np.array([1, 1, 2, 2, 2, 1, 1])
entropy_value = cluster_entropy(cluster_assignments, true_labels)
print("Overall clustering entropy:", entropy_value)
Follow-up Questions
How do we interpret a high entropy value versus a low entropy value in practice?
High entropy means that within each cluster, there is a greater mixture of points from multiple classes, indicating that the cluster boundaries do not align well with the true class labels. Low entropy implies that clusters tend to be composed of points from a small number of classes, suggesting a stronger alignment with ground-truth labels.
When might entropy not be an appropriate measure?
Entropy requires the existence of true labels. If the goal of clustering is purely exploratory (where no external labels are known), entropy cannot directly be used as an external validation measure. Furthermore, if clusters are imbalanced in size or if there are many tiny clusters, the results might be misleading, especially if small clusters artificially achieve very low entropy.
How does entropy compare to other external validation measures like Purity or Adjusted Rand Index?
Entropy and Purity are closely related; Purity measures the proportion of points in each cluster that belong to the most common class, while entropy considers the full distribution of classes in each cluster. Adjusted Rand Index compares how pairs of points are assigned in the clustering versus in the ground truth, which is a different perspective that can account for random chance. Each measure emphasizes different aspects of cluster quality, so the choice depends on which properties are most important for your task.
What about the logarithm base and its effect on the result?
Changing the base of the logarithm simply changes the unit of measurement (bits for base 2, nats for base e). It does not affect the relative comparison of entropies between different clustering solutions. Consequently, it does not alter how clusters rank in terms of homogeneity or impurity, though the absolute numerical value may differ.
How can entropy be extended if there are soft cluster assignments (where each data point can belong to multiple clusters with certain probabilities)?
In such cases, each data point has a probability distribution across different clusters rather than a single cluster assignment. One approach is to treat each data point’s membership in a cluster as weighted, then compute the corresponding p_{k,i} from these weights. The fundamental principle remains the same, but instead of a hard assignment, one aggregates membership probabilities.
How is the weighting by cluster size handled differently in practice?
Sometimes practitioners do a simple average of entropies across clusters. However, a weighted approach is often preferred because it accounts for the fact that a large cluster’s purity has a bigger impact on the overall quality than that of a small cluster.