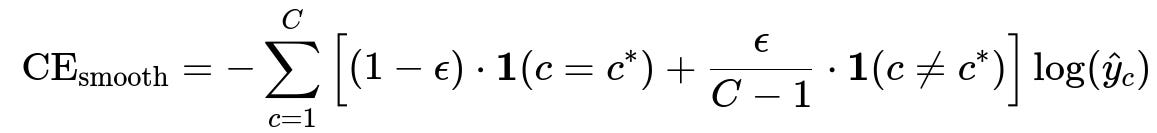ML Interview Q Series: How can label smoothing in classification tasks alter the landscape of the cross-entropy loss, and why might it improve generalization?

📚 Browse the full ML Interview series here.

Hint: It redistributes a small probability mass to incorrect classes.

Comprehensive Explanation

Label smoothing modifies the traditional one-hot label representation so that the correct class is not given a probability of 1.0 but rather 1 - epsilon (where epsilon is a small value, such as 0.1), and the remaining epsilon probability mass is spread equally among the other classes. This means that, instead of viewing the correct class as completely certain, the model is encouraged to respect a small degree of uncertainty. The key effect is that it reduces the model’s tendency to become overly confident in its predictions, which can improve both generalization performance and calibration.

In the usual cross-entropy setup for classification, the true label y_c is 1 for the correct class c=c^* and 0 for all other classes. When label smoothing is introduced, we replace y_c with a “smoothed” label distribution denoted as ỹ_c. The new cross-entropy loss with label smoothing can be represented by incorporating a small probability epsilon for each incorrect class:

Here:

• C is the total number of classes.

• epsilon is a small constant between 0 and 1.

• ỹ_c denotes the smoothed probability assigned to class c.

• c^* is the correct class index.

• hat{y}_c is the model’s predicted probability for class c.

• 1(...) is the indicator function that equals 1 if its argument is true and 0 otherwise.

Replacing the traditional 1 vs. 0 label with a softened label distribution forces the model to assign higher probability to the correct class, but not with absolute certainty. This can prevent extreme overfitting, where the model might latch onto spurious features to drive the loss toward zero. By ensuring that other classes receive a small but non-zero probability, the model is encouraged to maintain a smoother output distribution, which makes the training process more robust and helps in regularization.

This alteration of the loss landscape manifests as:

• A softer penalty for errors, because the target distribution is less “spiky.” This can reduce large gradients that could otherwise destabilize training.

• Reduced overconfidence, because when the model tries to make one class probability extremely high (close to 1), the slight penalty for ignoring the other classes entirely acts as a regularizer.

• Improved generalization, as the model can avoid memorizing labels to a perfect 1.0 probability and can adapt to variations in the data distribution more gracefully.

Label smoothing is used in state-of-the-art image classification models and text processing tasks, especially in large-scale models like Transformers. It is often a simple yet effective tweak that can yield better performance metrics and model calibration without significant computational overhead.

How It Differs from One-Hot Labeling

With pure one-hot labels, the loss pushes the model to assign probability 1.0 to the correct class and 0.0 to every other class. This drives very sharp decision boundaries and can encourage overconfidence, where the model can overfit to training samples and fail to generalize. Label smoothing, in contrast, gently penalizes overconfident assignments. By assigning a small probability to incorrect classes, the model is reminded that there is some possibility of alternative outcomes, even if very small.

Effect on Overconfidence and Calibration

A major benefit of label smoothing is better calibration. Calibration refers to how well a model’s predicted probabilities of an event reflect the true likelihood of that event. Overconfident predictions (e.g., always outputting 99% probability for the predicted class) can harm downstream tasks, particularly in scenarios that rely on well-formed probability estimates. With label smoothing, the predicted probabilities do not saturate as easily at 1.0, often leading to output distributions more in line with real-world likelihoods.

Implementation Example in Python (PyTorch)

import torch
import torch.nn as nn
import torch.nn.functional as F

class LabelSmoothingCrossEntropy(nn.Module):
    def __init__(self, epsilon=0.1, reduction='mean'):
        super(LabelSmoothingCrossEntropy, self).__init__()
        self.epsilon = epsilon
        self.reduction = reduction

    def forward(self, logits, target):
        # logits: (batch_size, num_classes)
        # target: (batch_size) with class indices
        num_classes = logits.size(1)

        # Convert target to one-hot
        with torch.no_grad():
            one_hot = F.one_hot(target, num_classes).float()
            # Apply label smoothing
            smooth_label = (1 - self.epsilon) * one_hot + self.epsilon / (num_classes - 1) * (1 - one_hot)

        log_probs = F.log_softmax(logits, dim=1)
        loss = - (smooth_label * log_probs).sum(dim=1)

        if self.reduction == 'mean':
            return loss.mean()
        elif self.reduction == 'sum':
            return loss.sum()
        else:
            return loss

This code shows a custom label smoothing cross-entropy loss in PyTorch. It transforms the target to a one-hot representation, then redistributes a fraction epsilon of the probability mass evenly across all incorrect classes.

Why It Improves Generalization

The reason label smoothing often enhances generalization is that the model does not overfit to a rigid, single-label distribution. By acknowledging that the true label distribution could have some uncertainty, the model’s parameters are encouraged to be less extreme. This prevents certain layers from developing excessively large weights solely to drive the predicted class probability toward 1.0 on every example. Empirically, this tends to reduce overfitting and leads to more robust performance on test data.

Potential Follow-Up Questions

What is the role of the epsilon hyperparameter, and how do you choose it?

Epsilon governs how much probability mass is subtracted from the correct class and distributed to incorrect classes. If epsilon is too large, the label distribution becomes too uniform, reducing the model’s ability to focus on the correct class. If epsilon is too small, the smoothing effect is negligible. Typical values range from 0.05 to 0.2, but exact tuning depends on the application and dataset. A common strategy is to start with a small epsilon like 0.1 and adjust based on validation performance.

Are there any scenarios in which label smoothing might hurt performance?

One scenario is when you need extremely sharp decision boundaries or when your training data has very little noise. Label smoothing can also interfere with certain loss functions or metrics that assume purely one-hot labels (for example, if you rely on exact 0 and 1 predictions for some post-processing). Additionally, if the dataset is already noisy or if you have confidence calibration mechanisms elsewhere, label smoothing could be redundant and might slightly degrade accuracy.

Can label smoothing be combined with other regularization techniques like dropout or weight decay?

Yes. Label smoothing is complementary to dropout, weight decay, and other forms of regularization. These methods operate at different levels: dropout regularizes the network by randomly dropping units, weight decay penalizes large weights, and label smoothing modifies the target distribution. Combining them can often enhance overall model robustness.

How is label smoothing different from mixup or other data-augmentation methods?

Label smoothing modifies the label distribution directly, without altering input data. Methods like mixup blend input examples and labels together, effectively creating new training samples. While both approaches smooth the training targets and can help with generalization, mixup changes the model’s input distribution as well as its label distribution. Label smoothing is simpler to implement, but mixup can sometimes offer a richer form of regularization by exposing the model to intermediate data points.

Could you use label smoothing in tasks other than classification?

While label smoothing is most commonly associated with classification, the same principle applies wherever one might want to avoid excessively peaky target distributions. For instance, in some sequence-to-sequence tasks (such as machine translation with Transformers), label smoothing can still be beneficial. The essential idea is to avoid training the model to be 100% certain of the next token. In segmentation tasks, label smoothing can also be applied class-wise to soften the ground-truth masks. The key is to ensure that your task naturally aligns with the notion of distributing probability mass across multiple classes or outputs.

How do you interpret the loss value when using label smoothing?

The absolute value of the cross-entropy loss might become smaller or larger compared to standard one-hot cross-entropy, because the targets are no longer purely 0 or 1. One should interpret the final loss in the context of its smoothed distribution. Comparing raw loss values between runs with and without label smoothing might not be entirely fair. Instead, rely more heavily on validation accuracy, F1 scores, or other performance metrics to judge improvements or regressions when introducing label smoothing.

Could label smoothing interfere with confidence-based metrics?

Label smoothing will typically reduce the maximum predicted probabilities, so metrics that rely on high-confidence predictions (for example, top-1 precision at a high probability threshold) might shift. However, in many practical scenarios, the improved calibration and reduced overfitting can still yield better overall performance. It is crucial to consider whether the application needs extremely confident predictions or well-calibrated probabilities.

These insights illustrate the typical reasoning behind label smoothing, how it influences the loss function, and the practical considerations for using it in training neural networks. It remains a robust technique for reducing overconfidence and improving generalization without adding much complexity to the pipeline.

Below are additional follow-up questions

How does label smoothing interact with class-imbalanced datasets, and what edge cases might arise?

Class-imbalanced datasets present a scenario where one or a few classes dominate in terms of sample count. Label smoothing can help by preventing the network from becoming too certain about the dominant class. However, if epsilon is chosen blindly, it can inadvertently over-smooth minority classes. In the presence of extreme imbalance, the minority classes already have fewer training examples, so excessively distributing probability to non-target classes can dilute the learning signal for these underrepresented classes. One subtle edge case is when some classes have very few instances and the model ends up treating them almost like random noise if epsilon is too large. To mitigate this, practitioners may choose a class-dependent smoothing scheme (e.g., smaller epsilon for minority classes or even skip label smoothing for certain underrepresented classes) to preserve a more distinct gradient signal.

Can label smoothing be adapted for multi-label classification, and if so, what are the pitfalls?

In multi-label classification, each instance can belong to multiple classes simultaneously. Traditional label smoothing spreads probability mass among classes under the assumption that the classes are mutually exclusive. For multi-label tasks, one might consider “softening” each label independently. For example, if an instance has k out of C possible labels, one approach could be to reduce the probability for the positive labels from 1.0 to 1 - epsilon, while the negative labels get a small probability of epsilon. A potential pitfall is that if you treat each label completely independently, you might lose important correlations among labels. Another subtle issue is that distributing epsilon among a large number of negative classes may dilute the signal for slightly ambiguous labels, especially if the dataset is already noisy. Ensuring that each label is still given sufficient weight remains critical for training success.

What if the training data contains mis-labeled examples or inherently noisy labels, and how does label smoothing behave in that context?

When labels are noisy or incorrect, label smoothing can actually help by making the model less confident about possibly erroneous examples. This extra uncertainty can reduce the harmful effect of mis-labeled samples, because the network does not attempt to perfectly fit a contradictory label. However, a significant pitfall arises if the noise level is extremely high. Label smoothing alone may not be enough to correct systematic labeling errors. In that case, more advanced strategies—like robust loss functions or semi-supervised learning with label correction—might be necessary. Additionally, if the distribution of noise is not uniform (e.g., certain classes are mislabeled more frequently), a uniform label smoothing strategy may not align well with the data’s true distribution of error, and it might require a more carefully tuned smoothing approach.

How do you measure the effectiveness of label smoothing beyond accuracy, and why might that matter?

Accuracy is a broad metric that may not fully capture nuances in predictive confidence. Metrics like calibration error (expected calibration error, or ECE) and log-likelihood (negative log-likelihood, or NLL) can provide additional insight. For instance, if the model’s accuracy remains the same but the calibration improves—meaning predicted probabilities better reflect actual occurrence frequencies—this can be critical in applications requiring reliable probability estimates (e.g., risk assessment). Another possibility is to monitor how predictions shift near decision thresholds. A well-calibrated model might produce more consistent predictions across different threshold settings. In certain domains like medical diagnostics, even if top-1 accuracy is unchanged, better probability calibration can directly impact clinical decision-making.

Could label smoothing cause problems in transfer learning scenarios or domain adaptation tasks, and why?

In transfer learning or domain adaptation, a model is first trained on a source domain and then fine-tuned on a target domain. If the source domain training employs label smoothing with a certain epsilon, it might learn a smoother decision boundary tailored to that domain’s label distribution. When switching to the target domain with different characteristics—class distributions, data styles, or label semantics—mismatched smoothing hyperparameters could hinder fine-tuning. For instance, if the target domain demands more certain predictions (perhaps it’s less noisy or has fewer classes), the previously smoothed decision boundary might slow convergence or degrade performance. Conversely, if the target domain is noisy and you did not apply any smoothing previously, you might not get the benefits of a softened decision boundary during fine-tuning. Practitioners may need to re-tune epsilon when transferring models between domains to avoid these pitfalls.

Does label smoothing impact model interpretability or explainability techniques such as saliency maps?

Model interpretability methods—like Grad-CAM or saliency maps—often rely on gradients to highlight which input features most influence the model’s predicted probability. Label smoothing affects gradients by limiting the incentive to drive a single class probability to 1.0, thus altering how the network balances competing classes. In some cases, this can make interpretations appear more “spread out,” reflecting the fact that no class is assigned absolute confidence. In practice, the changes to interpretability might be subtle, but in certain models or tasks, the reduced gradient magnitude toward a single class could produce less sharply defined saliency maps. This does not necessarily reduce the correctness of the interpretation, but it can change the visual or numerical patterns in ways that might require extra scrutiny when analyzing the model’s decisions.

Could label smoothing influence training speed or convergence properties, and how might one address issues that arise?

Label smoothing can speed up early convergence slightly by stabilizing gradients, especially in the presence of outlier examples that would otherwise cause large updates. However, in some architectures, smoothing might slow down the final push toward extremely high confidence in the correct class, resulting in longer epochs to plateau. If the dataset is large and well-curated, the smoothing effect might not be critical and could be reduced. Alternatively, you can implement a schedule for epsilon, starting with a moderate value and decaying it as training progresses. This dynamic approach allows label smoothing to stabilize learning early on but reduces constraints in later stages where the model can benefit from more confident boundaries. The main pitfall is choosing the correct schedule, as an overly rapid decay can negate the benefits of smoothing, while a too-slow decay might hamper final convergence to a sufficiently discriminative boundary.

How might you combine label smoothing with knowledge distillation, and what edge cases should you watch for?

Knowledge distillation uses a “teacher” model to provide soft targets for a “student” model. These soft targets contain information about relative class probabilities, which often helps the student generalize better than one-hot labels alone. Label smoothing can still be applied on top of or in conjunction with the teacher’s output distribution, but there is a subtlety: if the teacher model’s probabilities are already “soft,” additional smoothing might overly blur the target distribution. This can reduce the potential benefit of knowledge distillation, which is to convey the teacher’s nuanced distribution among classes. An edge case arises when the teacher model is extremely confident (e.g., near-1 probabilities for certain classes). In that scenario, label smoothing could help mitigate the teacher’s overconfidence, but if the teacher distribution already encodes meaningful relative probabilities, adding label smoothing might destroy some of that valuable information.

What role could label smoothing play in multi-head or multi-task learning setups?

Multi-head or multi-task learning setups typically have a shared backbone with multiple output heads for different tasks. If one of these heads is a classification task, label smoothing might improve its generalization. However, if another head is a regression or ranking task, the shared parameters might receive conflicting gradient signals—one head seeking very certain classifications, another head requiring precise continuous outputs. In practice, label smoothing can still help the classification head, but care must be taken that it does not overly dominate the shared layers at the expense of the other tasks. Sometimes, a different epsilon is used for each head if multiple classification tasks are involved, or label smoothing is disabled for particular tasks. One subtlety is that if the multi-task network receives conflicting demands (e.g., classification with label smoothing vs. regression that requires high sensitivity), the smoothing could limit the capacity of the shared representation to adapt for the regression head.

Are there any hardware or implementation details to keep in mind when integrating label smoothing at scale?

Label smoothing is relatively straightforward to implement, but at very large scales—such as distributed training on huge datasets—some details matter. One is numerical stability: the summation or multiplication of probabilities (1 - epsilon) and epsilon might lead to small floating-point inaccuracies when using mixed precision training. Another consideration is memory usage when one-hot encoding large batches for smoothing, especially if the number of classes is huge. This can be handled by directly computing the smoothed target distribution without fully expanding one-hot vectors in memory. Also, for extremely large-scale systems, communication overhead should be accounted for, especially if label distributions are broadcast across multiple GPUs or nodes. Although these issues are typically minor compared to the overall training overhead, they can still appear as subtle performance bottlenecks in high-throughput systems.