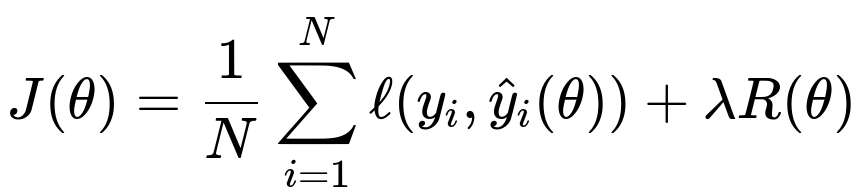ML Interview Q Series: How can the design of a cost function help avoid overfitting in deep neural networks without explicitly modifying the model architecture?
📚 Browse the full ML Interview series here.
Hint: Consider integrating penalty terms or adding constraints to the cost function.
Comprehensive Explanation
One of the most straightforward ways to avoid overfitting without changing a deep neural network’s architecture is to include additional terms or constraints in the cost (loss) function. Overfitting typically arises when a model fits too closely to the nuances and noise in the training data, failing to generalize to unseen data. By penalizing certain aspects of the model’s parameters or predictions, we can encourage better generalization without altering the network’s layer structure or other architectural components.
Role of Regularization Terms
A popular way to incorporate regularization into the cost function is to add a penalty term that penalizes large or complex parameter values. This modifies the overall loss to balance between fitting the training data and keeping the model’s weights constrained.
Where:
J(theta) is the overall cost function.
N is the number of training samples.
ell(y_{i}, hat{y}_{i}(\theta)) is the main loss term (for example, cross-entropy loss or mean squared error) for the i-th data sample.
theta refers to the trainable parameters (weights and biases) of the model.
R(theta) is the regularization term.
lambda is the regularization hyperparameter that balances the influence of the main data-fitting term and the regularization penalty.
Depending on the form of R(theta), different regularization strategies arise:
L2 Regularization (Weight Decay) This approach penalizes the sum of squares of the parameters, encouraging smaller weight values. The L2 penalty is especially common because it smooths the weight space and avoids overly large parameter estimates. In practice, it is typically referred to as weight decay in frameworks such as PyTorch or TensorFlow.
L1 Regularization (Lasso) This method penalizes the absolute values of the parameters. It encourages sparsity by driving many parameters toward zero, which can help with feature selection.
Group or Structured Regularization Variants like group Lasso aim to shrink entire sets of parameters together. This is particularly useful when dealing with structured data, or when we want to eliminate entire groups of weights rather than individual parameters.
Constraints on Parameters
Another way to embed regularization into the cost function is through constraints. Instead of (or in addition to) adding a penalty term, one might constrain the parameter vectors to belong to certain sets, such as a unit norm ball or a max-norm constraint. This ensures that the parameters do not exceed a certain magnitude, thereby mitigating overfitting. In some implementations, these constraints can be enforced by projecting weights back to the feasible set after each gradient update.
Label Smoothing as a Cost Function Technique
A popular technique in modern deep learning frameworks, particularly for classification tasks, is label smoothing, which modifies the target labels in the cost function. Instead of using one-hot encoded labels with 1.0 for the correct class and 0.0 for others, label smoothing replaces 1.0 with a value slightly less than 1.0 (for example, 0.9). This reduces the model’s confidence in its predictions, preventing it from overfitting to training labels. Label smoothing essentially acts as a regularizer on the final outputs rather than on the model parameters directly, yet it is still done through the loss function.
Practical Code Example (PyTorch)
import torch
import torch.nn as nn
import torch.optim as optim
# Suppose we have a simple neural network model
class SimpleNet(nn.Module):
def __init__(self, input_size, hidden_size, output_size):
super(SimpleNet, self).__init__()
self.fc1 = nn.Linear(input_size, hidden_size)
self.relu = nn.ReLU()
self.fc2 = nn.Linear(hidden_size, output_size)
def forward(self, x):
x = self.fc1(x)
x = self.relu(x)
x = self.fc2(x)
return x
# Create the model, define a standard loss like cross entropy
model = SimpleNet(input_size=100, hidden_size=50, output_size=10)
criterion = nn.CrossEntropyLoss()
# Add L2 penalty by specifying weight_decay in the optimizer
optimizer = optim.Adam(model.parameters(), lr=0.001, weight_decay=1e-4)
# Example training loop snippet
for epoch in range(10):
inputs = torch.randn(32, 100)
labels = torch.randint(0, 10, (32,))
optimizer.zero_grad()
outputs = model(inputs)
loss = criterion(outputs, labels)
loss.backward()
optimizer.step()
print(f"Epoch {epoch}: Loss = {loss.item()}")
In this example, weight_decay=1e-4 adds an L2 penalty to the cost function, which helps reduce overfitting by driving weights toward smaller magnitude.
Additional Insights
Since the question highlights that we do not modify the model architecture, it becomes critical to rely on methods that only tweak the objective function. Beyond simple L1 or L2 penalties, one can explore a variety of cost function techniques:
Confidence Penalties These techniques penalize over-confident predictions by adding a term to the loss function that encourages output probabilities to stay away from very high confidence values.
KL-Divergence with Soft Targets Instead of training purely with one-hot or hard labels, using soft targets or knowledge distillation approaches can regularize the model and prevent it from overfitting.
Mixup and Other Data-Centric Methods Although these typically involve data transformations, some are implemented at the loss level by mixing label distributions, acting in a similar spirit to label smoothing.
Possible Follow-up Questions
How do we choose the value of lambda?
Choosing the regularization coefficient lambda is typically done by validation-based hyperparameter tuning. One might run multiple experiments with different lambda values (for example, 1e-5, 1e-4, 1e-3, 1e-2) and select the one that yields the best validation set performance. In practice, lambda is often chosen using techniques such as grid search or a more sophisticated hyperparameter search (random search, Bayesian optimization, etc.).
What is the difference between L1 and L2 regularization in terms of behavior?
L1 and L2 regularization differ primarily in how they affect the distribution of learned parameters:
L2 tries to reduce large weights while still allowing many parameters to remain small but non-zero. This often leads to a smoother parameter space and is good for controlling overall magnitude without forcing sparsity.
L1 pushes many weights toward zero exactly, creating a sparse solution where some features become entirely irrelevant. This can lead to feature selection in linear models or compressed representations in deep nets. However, it might be trickier to optimize using gradient-based methods because the absolute value function has a non-differentiable point at zero.
Why do constraints like max-norm help?
Max-norm constraints limit the maximum norm of parameter vectors. This ensures that individual weight vectors do not become too large, which can reduce the model's capacity to memorize training examples. It also improves training stability, as excessively large weights can lead to exploding gradients or numerical instability.
Could we combine multiple penalties or constraints in one cost function?
Yes, it is possible to combine different penalties or constraints, although tuning multiple hyperparameters becomes more challenging. For example, one might use a small L2 penalty for all weights, plus a group Lasso penalty for certain blocks of weights if one has reason to believe that certain feature groups should be regularized as a unit. The key consideration is how these combined terms interact and how to balance their respective coefficients.
Does adding a penalty term always help?
Adding a regularization penalty helps in many practical cases but is not guaranteed to solve all overfitting issues. If the model is excessively complex or the dataset is very small and noisy, even strong penalties might not suffice. Regularization should usually be combined with a proper data collection strategy, data augmentation, and other best practices (such as early stopping) for optimal results.
Below are additional follow-up questions
How does regularization in the cost function affect the interpretability of the resulting model?
Regularization often pushes weight values toward smaller magnitudes or zero. In contexts where interpretability is crucial, such as in linear or sparse models, the penalization helps to highlight which features are truly important. For instance, L1 regularization can produce sparse weight vectors that zero out many coefficients. This makes it easier for a human to see which features have the greatest impact on the model. However, in deep neural networks, interpretability is not just about which weights are zero. The interplay of nonlinear activations and network depth can make interpretation more challenging. While regularization might reduce overfitting, it does not always produce a more “interpretable” model in a classical sense, because even small weights distributed across many neurons can represent complex patterns. One subtle pitfall is that while a model with an L1 penalty might appear more interpretable due to sparse weights, the actual behavior in terms of learned feature representations can still be intricate due to hidden layer transformations. Thus, the direct interpretability gains might be less than expected if the network is extremely deep and complex.
Are there scenarios where label smoothing may degrade performance rather than improve it?
Label smoothing replaces hard 1.0 labels with slightly less confident labels, often around 0.9, for the ground-truth class. This works well in many supervised learning setups because it avoids overconfident predictions and adds a mild regularizing effect. In some scenarios, however, label smoothing can be detrimental:
Highly imbalanced datasets: If your dataset is severely imbalanced, you might already be struggling to get the model to be sufficiently confident on the minority class. In such a situation, label smoothing might reduce critical certainty on rare classes, thus harming overall performance.
Tasks requiring absolute certainty: Certain tasks, such as specific anomaly detection or specialized medical diagnoses, might require the model to be as confident as possible when it identifies certain patterns. Label smoothing can undercut that certainty.
Very small datasets: If the dataset is extremely small, artificially reducing the confidence might lead to a less stable training process, especially if each example is already precious for learning fine distinctions.
What is the relationship between learning rate and the effect of regularization penalties in the cost function?
The learning rate controls how quickly parameters are updated toward the gradient direction during training. A regularization penalty, such as an L2 term, will also shift the gradient. If the learning rate is too large, the effect of the regularization term might be overshadowed by large parameter updates from the main loss. This makes the weight decay less noticeable early in training. Conversely, if the learning rate is very small, the model might adhere more tightly to the penalty term and converge more slowly to an optimal solution. The subtlety arises with adaptive optimizers (like Adam or RMSProp), which dynamically adjust learning rates for each parameter. If some parameters experience bigger gradient updates than others, the effectiveness of the regularization penalty could vary across weights. A pitfall occurs if one incorrectly sets a large learning rate while also using strong weight decay, thinking that both will “cancel out.” In reality, the strong penalty might prevent the model from learning crucial patterns, or the large learning rate might continually override the regularization. Balancing these hyperparameters typically requires validation-based tuning.
How does data imbalance interact with regularization methods added to the cost function?
When dealing with imbalanced datasets, regularization might inadvertently penalize the model in ways that skew its focus. Standard penalties such as L2 do not directly account for class distribution; they merely constrain weight magnitudes. If the model is already biased toward predicting the majority class, a strong regularizer might push weights further toward a simplistic solution that neglects minority classes. One edge case arises when the minority class is so small that the network’s capacity is not truly challenged in learning majority-class patterns. In such scenarios, if you apply too much regularization, the model may oversimplify and largely ignore minority-class examples. Balancing regularization with techniques like class weighting, oversampling the minority class, or data augmentation is crucial to achieve good performance on all classes.
How do penalty terms compare to data augmentation approaches for avoiding overfitting?
Penalty terms and data augmentation both help mitigate overfitting, but they operate at different levels. Regularization terms in the cost function typically target the model parameters (e.g., penalizing large weights or encouraging sparsity). Data augmentation addresses overfitting by injecting additional diversity into the training data, effectively teaching the model a broader set of examples. Data augmentation can be especially effective in image, speech, or text domains where transformations (cropping, flipping, masking) preserve the underlying label. However, it may not always be straightforward to design augmentations for structured tabular data or highly specialized tasks. Regularization, on the other hand, can be applied to almost any model without requiring domain-specific transformations. In practice, data augmentation and penalty-based regularization are complementary. A pitfall arises if one assumes that heavy data augmentation alone can control overfitting for extremely large or deep models. In fact, combining data augmentation with well-chosen penalty terms frequently yields better results than relying on one approach exclusively.
Can different layers or parts of the network have different forms or strengths of regularization?
Yes, you can apply different regularization schemes or strengths to different parts of a neural network. One common approach is to put strong regularization (like a larger L2 coefficient) on the final classification layer or fully connected layers, while applying weaker regularization to earlier convolutional layers (in the case of a CNN). The rationale is that later layers often have a larger number of parameters and can more easily overfit. A subtlety arises with multi-task networks or networks that have multiple heads for different tasks. Sometimes you want heavy regularization on the shared backbone so that it generalizes well across tasks, but a lighter penalty on task-specific heads so that each task can more easily adapt. The main challenge is tuning the separate regularization strengths. Over-regularizing key layers can limit capacity too much and harm performance, while under-regularizing can lead to overfitting in certain parts of the network.
What strategies can be employed if we observe underfitting while a penalty term is in place?
If a network is underfitting, it indicates that the model is not capturing the underlying patterns in the data. If you are already using a penalty term (like L2 or L1) and you see underfitting, possible strategies include:
Reduce the strength of the penalty: Lower the lambda value for L2 or L1 regularization to allow the network more flexibility in adjusting its parameters.
Use a more suitable penalty type: Sometimes switching from L2 to L1 (or vice versa) can help, depending on whether you need sparse solutions or prefer to spread smaller weights across many neurons.
Collect more training data or reduce data noise: If the data is not representative or contains inconsistencies, even a well-parameterized model with mild regularization might fail.
Increase model capacity or change architecture: Although the question focuses on not modifying the architecture, if underfitting persists, you may need to ensure that the model has enough capacity to learn the data distribution. An important pitfall is that increasing model complexity or removing regularization might indeed fix underfitting in the short term, but it can also open the door to overfitting in the long run unless carefully monitored with validation data or early stopping.
How does one handle overfitting in large-scale language models through cost function design alone?
Large-scale language models, such as transformers with hundreds of millions or billions of parameters, can easily overfit if not properly regularized. While architectural choices like dropout are popular, you can also employ cost function design to control overfitting:
Weight decay (L2 penalty): Commonly used in transformer-based language models. Tuning the coefficient can significantly impact model generalization.
Label smoothing: Often used in sequence-to-sequence tasks (e.g., machine translation). It can help reduce overconfidence in predicting the next token.
Adversarial or consistency-based regularization: Though more advanced, these methods inject adversarial perturbations or enforce consistent predictions under small input perturbations. This can be framed through specialized loss terms that penalize divergences. One subtlety is that large-scale language models are typically trained with massive datasets, so they might not overfit in the conventional sense. Instead, they might exhibit memorization of certain dataset artifacts. Properly tuning the penalty terms, as well as monitoring potential memorization of sensitive training data, becomes critical.
In what ways can we design cost functions to incorporate fairness or bias constraints for certain protected groups?
Modern machine learning applications sometimes require constraints to address fairness and bias against protected groups. While not strictly a traditional form of overfitting control, fairness constraints or penalty terms can also be integrated directly into the cost function. For instance, one might add a term that penalizes discrepancies in false-positive or false-negative rates across different demographic groups. A typical approach is to define a metric (e.g., demographic parity, equalized odds) and then incorporate a penalty if the model deviates from that metric across groups. This effectively modifies the optimization objective to both fit the data and maintain fairness criteria. A potential pitfall is that adding multiple constraints can make the optimization landscape more complex. The network may not converge easily if fairness penalties conflict strongly with predictive performance on the primary objective. Moreover, the data distribution itself might be skewed, making fairness-based penalties insufficient if deeper structural biases exist in the dataset.
How might we detect if our chosen regularization term is having an unintended effect on certain subpopulations or edge cases in the data?
Monitoring aggregate accuracy or loss might not reveal how different subpopulations or unusual data samples are affected by the penalty. For instance, if a subpopulation requires large weight coefficients to be predicted accurately, L2 or L1 penalties might disproportionately harm performance on that group. A practical strategy is to analyze performance metrics separately for various subpopulations. If one group’s accuracy or F1 score systematically degrades after applying a particular penalty, that is a signal you might need a more nuanced approach—perhaps using group-specific regularization or adjusting the data pipeline. An edge case is when the subpopulation is very small. The penalty might force the network to ignore that subgroup’s unique patterns altogether. Another edge case is when the regularization penalty interacts with data imbalance. Weight decay might push the solution to favor majority-class patterns and neglect rare subpopulations.