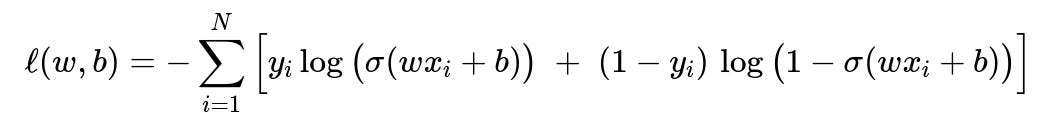ML Interview Q Series: How can we arrive at a mathematical understanding of how Logistic Regression works?
📚 Browse the full ML Interview series here.
Comprehensive Explanation
Logistic regression is a classification model that predicts the probability of a sample belonging to a certain class. It does this by modeling the log-odds of the probability as a linear combination of the input features. Below is a detailed breakdown of its mathematical intuition and the reasoning behind it.
Core Mathematical Concepts
At the heart of logistic regression is the logistic (sigmoid) function, which converts a linear input into a probability between 0 and 1. Suppose the model parameters are w (the weight vector) and b (the bias), and x is the feature vector. A linear combination of the input features is z = w x + b. This linear term z is then fed into the sigmoid function to obtain a probability estimate that y = 1.
Here, z = w x + b. The sigmoid function ensures the output remains in the (0, 1) range.
Interpretation of the Sigmoid Function
When z is very large (positive), e^(-z) is almost 0, so the sigmoid is close to 1.
When z is very large (negative), e^(-z) becomes large, making the sigmoid output close to 0.
When z = 0, the sigmoid function value is exactly 0.5.
In effect, logistic regression uses the log-odds representation: log( p/(1 - p) ) = z, where p is the probability that the sample belongs to the positive class.
Loss Function and Maximum Likelihood
A common way to train logistic regression is through maximum likelihood estimation. Given a dataset of N samples (x_i, y_i), where y_i in {0,1}, we use the concept of likelihood to optimize w and b. The likelihood is the probability of observing all training labels given the inputs.
If p_i is the predicted probability that y_i = 1, then:
p_i = sigma( w x_i + b ).
We want to maximize the product of correct probabilities for all training samples:
Product over i of [p_i^y_i * (1 - p_i)^(1 - y_i)].
It is more convenient to work with the negative log-likelihood (which is turned into the cross-entropy loss). Minimizing this is equivalent to maximizing the likelihood.
In this expression:
y_i is the observed label (0 or 1).
sigma(w x_i + b) is the predicted probability that y_i = 1.
The summation runs over all training examples i from 1 to N.
Parameters Explanation for the Loss Function
w x_i + b is the linear score for sample i.
sigma(...) is the sigmoid function applied to that linear score.
y_i log(p_i) + (1 - y_i) log(1 - p_i) is the log-likelihood term for binary classification.
The negative sign means we are minimizing -log-likelihood (i.e., we are maximizing log-likelihood).
Gradient-Based Optimization
To find the parameters w and b that minimize this loss, we typically use gradient-based methods like Gradient Descent or variants such as Stochastic Gradient Descent (SGD) or Adam. The gradient of the cross-entropy loss with respect to w and b is straightforward to compute using the chain rule. This ease of optimization is one of the reasons logistic regression is widely used in practice.
Decision Boundary
In logistic regression, the decision boundary occurs where the model's output probability is 0.5. Since sigmoid(z) = 0.5 when z = 0, our decision rule effectively becomes: predict class 1 if w x + b >= 0, otherwise class 0. This shows that logistic regression is a linear classifier in the original input space.
Example Python Snippet
Below is a minimalistic example in Python (using NumPy) to illustrate how one might implement logistic regression from scratch. This code uses batch gradient descent for simplicity:
import numpy as np
# Simple synthetic dataset
X = np.array([[0.1, 1.2],
[1.0, 0.4],
[2.5, 3.1],
[3.0, 1.1],
[2.2, 2.3]])
y = np.array([0, 0, 1, 1, 1])
# Initialize parameters
w = np.zeros(X.shape[1])
b = 0.0
def sigmoid(z):
return 1.0 / (1.0 + np.exp(-z))
# Training hyperparameters
learning_rate = 0.1
epochs = 1000
for epoch in range(epochs):
# Compute linear combination
z = np.dot(X, w) + b
# Sigmoid for predicted probability
p = sigmoid(z)
# Gradient of the loss wrt parameters
dw = np.dot(X.T, (p - y)) / len(y)
db = np.sum(p - y) / len(y)
# Update parameters
w -= learning_rate * dw
b -= learning_rate * db
print("Trained weights:", w)
print("Trained bias:", b)
In practice, one might use machine learning libraries like scikit-learn, PyTorch, or TensorFlow to perform the optimization more efficiently, especially for large-scale data.
Potential Follow-Up Questions
Could you explain why logistic regression outputs can be interpreted as probabilities?
The sigmoid function ensures the output ranges between 0 and 1, matching the range of a probability. Additionally, by treating the class label as a Bernoulli random variable and applying maximum likelihood estimation, we effectively tie the model’s output to a probabilistic interpretation. The logistic transformation of the linear combination (w x + b) into [0,1] makes logistic regression a natural choice for modeling probability of belonging to a class.
How do we handle overfitting in logistic regression?
Overfitting can be mitigated by:
Regularization: Often L2 regularization is used by adding a term lambda * sum(w_j^2) to the loss. This encourages smaller weights and reduces variance.
Feature selection: Removing or combining correlated features can help reduce model complexity.
Data augmentation or acquiring more training samples: More data can often help the model generalize better.
Is logistic regression suitable for non-linear boundaries?
Logistic regression uses a linear function inside the sigmoid. This makes the decision boundary linear in the original feature space. If the underlying classes are not linearly separable, logistic regression might struggle. One can address this by manually engineering non-linear features (e.g., polynomial features) or using kernel methods. Alternatively, one can switch to more flexible models, such as neural networks, decision trees, or kernel-based SVMs.
Can logistic regression handle imbalanced datasets?
Yes, but it might require additional care, such as:
Class weighting: Adjusting the loss by giving more weight to minority class samples.
Oversampling or undersampling: Making sure the model sees a balanced proportion of each class.
Using appropriate metrics like Precision, Recall, or F1-score instead of accuracy, to properly evaluate performance on imbalanced data.
Why do we use cross-entropy loss for logistic regression instead of mean-squared error?
Mean-squared error (MSE) can lead to undesirable local minima and slower convergence in the context of logistic regression. Cross-entropy is the natural loss for probabilistic classifiers modeled with the Bernoulli distribution assumption. It aligns better with maximum likelihood estimation and typically converges faster while providing reliable gradient signals.
Does logistic regression assume features are independent?
There is no explicit assumption that features must be statistically independent in logistic regression the way it is assumed in naive Bayes classifiers. However, logistic regression does assume that the log-odds are a linear function of the input features. If there is a dependence structure among features that violates the linearity assumption in the log-odds space, the model may underperform, unless additional feature engineering is done.
How does logistic regression compare to a small neural network?
A single neuron with a sigmoid activation is essentially performing logistic regression. A neural network with hidden layers, however, allows for complex non-linear boundaries. Logistic regression is typically easier to interpret since it is a linear model in the log-odds space, and the model parameters have a direct meaning in terms of feature influence.
How would you interpret the coefficients in logistic regression?
The coefficients (w_j) correspond to the log-odds changes of the positive class for every 1-unit change in the feature x_j, holding other features constant. A positive coefficient increases the log-odds (thus increasing the probability), while a negative coefficient decreases the log-odds. The bias term b corresponds to the log-odds baseline when all features are zero.
What if the dataset has outliers or extreme values?
Logistic regression can be impacted by outliers, especially if they significantly distort the linear relationship in the log-odds space. Regularization can mitigate this. Alternatively, robust regression methods or data preprocessing (e.g., outlier removal) might be employed if we suspect outlier contamination.