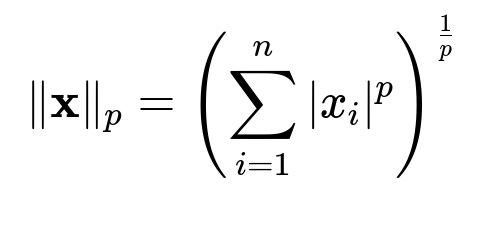ML Interview Q Series: How can we quantify or measure the magnitude of a vector in different ways?
📚 Browse the full ML Interview series here.
Comprehensive Explanation
In mathematics and machine learning, it is often crucial to quantify the size or length of vectors, because this measure underpins various algorithms and theoretical results. The most common approach to measuring vectors involves using norms, which generalize the idea of “distance” or “magnitude” in different ways. A norm must satisfy specific properties such as non-negativity, homogeneity (scaling), and the triangle inequality.
A very general family of norms is the Minkowski (p-norm) family. This family allows a parameter p that changes how we measure the vector’s magnitude. It includes the most commonly encountered norms in practice.
Minkowski (p-Norm)
The Minkowski p-norm for a vector x in R^n, when p >= 1, is given by:
Here x is a vector in R^n, x_i is the i-th component of x, n is the dimensionality of the vector, p is a real value >= 1, and |x_i| represents the absolute value of component x_i. This norm returns a non-negative scalar that captures the magnitude of x in a manner dependent on the parameter p.
Common Vector Norms
Below are some widely used norms (all members of the Minkowski family except the L0 measure, which is not technically a norm but is sometimes considered for certain applications):
L1 Norm This is obtained by setting p=1 in the Minkowski norm. In text-based form, ||x||_1 = |x_1| + |x_2| + ... + |x_n|. This norm is known as the Manhattan distance or Taxicab norm. It emphasizes sparsity in many machine learning contexts. In high-dimensional models, L1 is often used for regularization (LASSO) because it promotes zero coefficients.
L2 Norm For p=2, we get the Euclidean norm: ||x||_2 = sqrt(x_1^2 + x_2^2 + ... + x_n^2). This is the most familiar norm, directly related to geometric distance in Euclidean space. In ML, L2 is used for regularization (Ridge regression) and many loss functions are based on squared Euclidean distance.
L∞ Norm This norm (sometimes called the max norm) can be seen as the limit of the Minkowski norm as p approaches infinity. In plain text, ||x||_∞ = max_i |x_i|. It looks at the largest absolute component of a vector. This is sometimes useful in optimization or worst-case (robust) scenarios.
L0 "Norm" In many ML tasks, especially feature selection, we consider the number of non-zero elements in a vector. Although it is usually called an L0 measure, it is not a proper norm mathematically, because it does not satisfy the triangle inequality. It is, however, extremely useful when one wants to encourage many elements of a parameter vector to be exactly zero.
Other Measures Different distance metrics and norms exist depending on the application. For instance, the Mahalanobis distance modifies the measure of distance based on correlations between components of x. There can also be specialized weighted norms if different dimensions need different scales.
Practical Uses in Machine Learning
The choice of norm can significantly affect the performance and interpretability of ML models:
L2-based methods (like Ridge) tend to distribute shrinkage across coefficients smoothly.
L1-based methods (like LASSO) encourage sparsity, which aids in feature selection.
Using L∞ or other norms can help design robust approaches that focus on the largest deviation in data.
Follow-up Questions
What is the difference between L1 and L2 norms in high-dimensional ML applications?
In high-dimensional spaces, L2 spreads out the penalty across all coefficients. This makes parameters shrink toward zero but not exactly hit zero, often leaving many small but non-zero weights. In contrast, L1 norm tends to push weaker coefficients to be exactly zero, effectively performing feature selection by turning some weights off. From a geometric view, the L1 norm creates a diamond-shaped contour in coefficient space, whereas the L2 norm creates a spherical contour. When these contours intersect with the feasible region, L1 tends to catch corners, which correspond to zero solutions for some coefficients.
How does L1 regularization encourage sparsity?
The L1 norm regularization adds |w_i| to the loss function for each parameter w_i. The corner (or edge) geometry of the L1 penalty means it is “cheaper” (in terms of cost-minimizing solutions) to force some parameters exactly to zero than to spread small magnitude changes across all parameters. This geometric property contrasts with L2 norms, which penalize large coefficients more heavily but do not force them to zero.
Why might we prefer L∞ norm in certain optimization problems?
The L∞ norm (max norm) can be valuable in robust optimization scenarios where controlling the maximum deviation is critical. One example might be bounding the worst-case change in a parameter vector or bounding the maximum absolute deviation in weights for interpretability. In adversarial settings, sometimes focusing on a single large deviation can align better with real-world constraints.
Could you explain the Mahalanobis distance in more detail?
Mahalanobis distance is not strictly a simple norm of x but rather a distance metric that takes into account the covariance structure of the data. Its formula in plain text-based form is sqrt((x - mu) transposed * Sigma_inverse * (x - mu)), where mu is the mean vector and Sigma_inverse is the inverse of the covariance matrix. It effectively scales and rotates the input space so that distances are measured in units of the data’s own variance along each direction. This can be especially important when features have varying scales or correlations.
How can one decide which norm to use for model regularization?
This choice usually depends on prior knowledge, the nature of the data, the interpretability requirements, and computational considerations.
L2 is often standard and simpler to optimize due to differentiability.
L1 is a good choice for feature selection and sparsity, though it can be more challenging to optimize.
Other norms or distances might be needed for domain-specific reasons, such as handling heavy correlation or outliers robustly.
Can we directly optimize for L0 norm solutions?
Directly optimizing with the L0 measure is computationally difficult (NP-hard in many scenarios) because it involves discrete combinatorial search (either a parameter is zero or not). Hence, approximate or surrogate techniques (like using L1) are adopted in practice. Another approach is to use iterative methods that approximate the L0 cost, but these can still be quite expensive and require specialized algorithms.