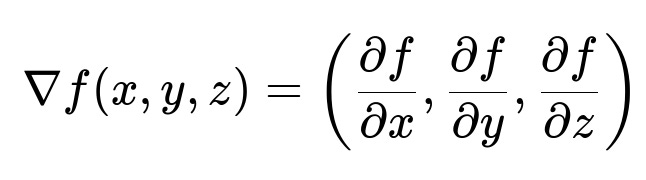ML Interview Q Series: How can we determine the normal vector for the given surface S described below?

📚 Browse the full ML Interview series here.

Comprehensive Explanation

One of the most common ways to describe a surface S in three-dimensional space is by using an implicit function f(x, y, z). That is, we define S as all points (x, y, z) satisfying the equation f(x, y, z) = 0. If S is given in this form, then the normal vector at any point on S can be computed by taking the gradient of f.

When we say gradient, we mean the vector of partial derivatives of f with respect to each spatial variable x, y, z. This gradient vector is orthogonal (perpendicular) to the surface, and hence points in the direction normal to S at that location.

In the above expression, partial f / partial x is the partial derivative of f with respect to x, partial f / partial y is the partial derivative with respect to y, and partial f / partial z is the partial derivative with respect to z. Evaluated at a specific point (x, y, z) on the surface, this gives a vector that points normal to S.

If a surface is expressed parametrically instead, for example r(u, v) = (x(u, v), y(u, v), z(u, v)), you can find the normal by taking the cross product of the partial derivatives of the parameterization with respect to u and v. Specifically, partial r / partial u cross partial r / partial v will yield a vector normal to the surface.

To get a unit normal, you would normalize the resulting vector by dividing by its magnitude. In many geometric and physical contexts, only the direction of the normal matters, but there are situations (like flux computations) where the magnitude also matters, so it is important to keep track of whether you are using the raw gradient or a normalized version.

What if the surface is given in explicit form, like z = g(x, y)?

If the surface is given as z = g(x, y), you can rewrite it implicitly as f(x, y, z) = z - g(x, y) = 0. Then the gradient of f is partial f / partial x = -partial g / partial x, partial f / partial y = -partial g / partial y, partial f / partial z = 1. Evaluating these partials yields the normal direction at any point (x, y, z).

Why does the gradient vector point in the normal direction?

The gradient of an implicit function f(x, y, z) points in the direction of greatest rate of increase of f. Along the surface f(x, y, z) = 0, infinitesimal changes that keep you on the surface do not change the function value (because f remains 0). Therefore, those tangent directions lie in the subspace where f(x, y, z) does not vary. The direction in which f changes is by definition perpendicular to those tangent directions, making it the normal direction.

How do we deal with sign or direction ambiguity in the normal vector?

The gradient can point in “either” outward or inward direction, especially in closed surfaces. If your problem setup requires an outward normal (such as in certain boundary integration tasks), you typically choose the sign so it points outward. In other situations, you might pick the sign for consistency in orientation. The essential point is that both +n and -n are normal to the surface.

Does the magnitude of the gradient matter when determining the normal?

The normal direction is always given by the gradient direction, but the magnitude of the gradient can differ at different points on the surface. If you want a unit normal, you can normalize by dividing by the vector’s magnitude. If your application (like flux or geometry factor computations) requires the normal to represent more than a direction, you might keep the gradient unnormalized so that it encodes local geometric information.

How would you implement a normal vector calculation in Python?

Below is a short example that demonstrates how one might compute the gradient and hence the normal at a point for a function f(x, y, z). Suppose we have f(x, y, z) = x2 + y2 + z**2 - 1. Then the surface f(x, y, z) = 0 is a sphere of radius 1.

import sympy

# Define the variables
x, y, z = sympy.symbols('x y z', real=True)

# Define the function f
f = x**2 + y**2 + z**2 - 1

# Compute the gradient
grad_f = (sympy.diff(f, x), sympy.diff(f, y), sympy.diff(f, z))

# Suppose we want the normal at the point (0.5, 0.5, sqrt(0.5))
# Evaluate the partial derivatives at that point
point = {x: 0.5, y: 0.5, z: (0.5**0.5)}
normal_vector = [g.evalf(subs=point) for g in grad_f]
print("Normal Vector:", normal_vector)

# If we need a unit normal, we normalize
import math
magnitude = math.sqrt(sum([comp**2 for comp in normal_vector]))
unit_normal = [comp/magnitude for comp in normal_vector]
print("Unit Normal:", unit_normal)

This code uses Sympy to symbolically compute partial derivatives and then evaluate at a specific point on the surface. The computed normal_vector is the gradient, and unit_normal is the direction of that gradient normalized to length 1.

Additional Follow-Up Questions

Can the normal vector change dramatically near points where the gradient is small or zero?

Yes, if at some point (x, y, z) on S, the gradient is zero, this implies either a singularity or a critical point. Normally, well-defined surfaces do not have gradient zero on a smooth patch, unless you have a cusp, corner, or other degeneracy. In practical applications, these points can be tricky because the concept of a well-defined normal might break down or require special handling.

If the surface is given as an intersection of two surfaces, how do we find a normal vector?

You can treat each constraint as f1(x, y, z) = 0 and f2(x, y, z) = 0. The normal to the intersection curve of these two surfaces is orthogonal to both ∇f1 and ∇f2. Hence, you often take the cross product of ∇f1 and ∇f2 to get a direction that is tangent to the curve of intersection. For the surface normal in such multi-constraint situations, you usually look at the geometry problem more carefully, because an intersection might not itself define a single normal the same way a single surface does.

How do I decide which method (gradient or cross product of partial derivatives) to use for normal vector calculation?

If you have an implicit equation f(x, y, z) = 0, use the gradient approach. If you have a parametric equation r(u, v) for the surface, use the cross product of the partial derivatives. Both yield valid normal directions but depend on the style of the surface representation.

What if I am computing flux integrals or surface integrals, do I need a unit normal?

For surface integrals of a scalar field (where you just need oriented area), the magnitude of the normal matters because dS is typically the magnitude of that cross product or the magnitude of the gradient-based vector times the differential area. Depending on the integral, you might see integrands that include dot products with vector fields. In these cases, you should ensure you are using the correct orientation and magnitude of the normal. Sometimes you will see an integral defined with n as a unit normal, but also multiplied by some Jacobian factor if the parameterization is used. It all depends on the integral’s specific definition.

These considerations illustrate why having a thorough understanding of how to calculate normal vectors—and how the gradient or cross product methods relate to your specific application—is vital in mathematics, physics simulations, and computer graphics applications.