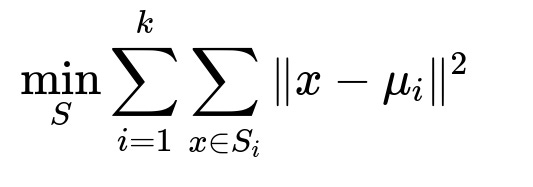ML Interview Q Series: How can you efficiently apply k-Means clustering when working with extremely large datasets?
📚 Browse the full ML Interview series here.
Comprehensive Explanation
k-Means clustering aims to partition data points into k distinct groups by minimizing the sum of squared distances between each data point and its assigned cluster center. The fundamental objective can be represented by the function below.
Here, k is the total number of clusters, S_{i} denotes the set of data points that belong to cluster i, x is an individual data point, and mu_{i} is the centroid (center) of cluster i. The algorithm iterates between assigning points to their nearest centroids and updating each centroid as the mean of the assigned points until convergence or for a fixed number of iterations.
When dealing with extremely large datasets, the traditional k-Means approach can be very expensive in terms of time and memory. Some effective strategies and considerations for large-scale k-Means clustering are given below.
Using Mini-Batch k-Means or Online Variants
Traditional k-Means requires multiple passes over the full dataset in each iteration, which is often infeasible when the data is extremely large. Mini-Batch k-Means processes small batches of data (for example, a few hundred or thousand points at a time), updating the centroids after each batch. This significantly reduces memory usage and can converge to a good approximation in far less time than the standard batch algorithm. There are also online variants of k-Means that continuously update centroids as each new point comes in, making them suitable for streaming scenarios.
Leveraging Approximation and Sampling
In many real-world problems, uniformly sampling a subset of data can be an effective way to reduce computational load. One can run full k-Means on the sampled subset, then fine-tune the centroids by reassigning all data points to those centroid positions and possibly performing minimal additional updates. While this approach introduces approximation, in practice, if the sample is representative, it is often sufficiently accurate and computationally inexpensive.
Distributed and Parallel Frameworks
Modern large-scale data processing platforms (for instance, Spark) allow parallel execution of machine learning tasks. The data can be partitioned across multiple nodes, and partial statistics (like partial sums of points for each cluster) can be aggregated. By combining the partial updates from different nodes, you can update the global centroids in each iteration. This approach takes advantage of cluster computing infrastructures, scaling out k-Means to handle billions of data points.
Dimensionality Reduction
When data is extremely high-dimensional, dimensionality reduction techniques such as PCA or autoencoders can simplify the data. Lower-dimensional representations often preserve enough of the essential structure to allow efficient clustering. This can further speed up k-Means, though you must carefully verify that the reduced representation captures the variance needed to form meaningful clusters.
Efficient Data Storage and Access
When data resides in distributed file systems or large data warehouses, it is essential to reduce expensive data movement. Strategies like performing computations in-place or moving only summaries of data (rather than all raw data points) can be instrumental in making k-Means scalable. Data layout choices also matter; using compressed or columnar formats might reduce I/O overhead.
Monitoring Convergence and Early Stopping
It may be beneficial to place a limit on the number of iterations and stop if the change in centroid positions is below a threshold. For enormous datasets, even a small movement of centroids each iteration can be computationally expensive, and in many practical situations, near-convergence solutions are good enough.
Practical Example: Mini-Batch k-Means in Python
from sklearn.cluster import MiniBatchKMeans
import numpy as np
# Assume X is your large dataset: a NumPy array or something similar
# Here we generate random data just for demonstration
X = np.random.rand(1000000, 10) # 1 million rows, 10 features
mini_batch_kmeans = MiniBatchKMeans(n_clusters=10,
batch_size=1000,
max_iter=100) # Limit iterations
mini_batch_kmeans.fit(X)
print("Cluster centers:")
print(mini_batch_kmeans.cluster_centers_)
This example processes the data in small increments of 1000 points. Memory usage remains relatively low, and the model updates the cluster centers with each mini-batch.
How does mini-batch k-Means differ in complexity from the standard batch version?
Standard k-Means typically needs repeated passes over the entire dataset. Suppose you have N data points, D dimensions, and k clusters. The complexity per iteration is usually on the order of O(k N D). With many iterations, this becomes cumbersome for large N.
Mini-Batch k-Means processes only a small batch b of points each iteration. The complexity per iteration becomes approximately O(k b D), which is often far smaller, since b << N. Although more iterations might be required, the overall time can be significantly reduced, and memory usage is also far more manageable.
What are the trade-offs when using approximations and sampling methods?
While sampling reduces computational load, it is possible to miss some outliers or underrepresented portions of the dataset, which could produce suboptimal cluster centers. The trade-off is between computational feasibility and precision. In most large-scale use cases, a carefully chosen sampling strategy or mini-batch approach provides an acceptable approximation to the full solution without incurring the cost of processing every data point in every iteration.
How can distributed k-Means handle synchronization and communication overhead?
In a distributed setup, data is partitioned across multiple workers. Each worker can compute partial statistics such as the sum of all data points assigned to each cluster and the total number of points in each cluster. These partial results are then aggregated to update the global centroids. Communication overhead involves transferring the partial updates between workers and the central node. If updates happen too frequently or the network is slow, the communication overhead can be significant. Striking a balance by batching updates, limiting iteration counts, or hierarchically aggregating updates can help mitigate these issues.
How do you ensure the correct number of clusters for large datasets?
Choosing k is always a challenging issue in k-Means. Techniques such as the elbow method, silhouette scores, or more advanced methods like the gap statistic can guide the choice. However, for very large datasets, repeatedly running clustering with different k values can still be expensive. An alternative is to adopt hierarchical or progressive techniques. For instance, start with a rough guess, observe cluster separation, and adjust k if needed. Or build a hierarchical structure (like a tree of cluster centroids) and prune or expand branches based on validation metrics.
What potential problems arise if data is streaming or time-dependent?
Streaming data requires updating clusters on the fly. Online k-Means treats each incoming data point (or small batches) as an opportunity to adjust the cluster centers. This is beneficial when the data distribution shifts over time. However, you have to carefully tune the learning rate or the rate at which new points overwrite older centroid information to avoid noisy updates or overly slow adaptation to new trends.
What if k-Means is not the right clustering approach?
k-Means assumes roughly spherical, equally sized clusters in continuous space. In scenarios involving clusters of highly varying densities or non-spherical shapes, algorithms like DBSCAN or hierarchical clustering might be more suitable. For very large data, these alternatives can also be challenging, but they handle data distributions that violate k-Means assumptions more gracefully.
Are there any initialization concerns for large datasets?
Poor centroid initialization can lead to slow convergence or suboptimal solutions. Methods like k-means++ can help choose better initial centers by probabilistically spreading them out in proportion to distance. Even so, for very large datasets, initialization must avoid scanning the entire data. One approach is to sample a subset of points, run k-means++ on that subset, and scale up the results.
How do you evaluate the clustering quality with very large data?
Evaluating clustering quality often requires computing metrics such as inertia or silhouette scores, which involve iterating over the entire dataset. When the data is massive, you can either resort to sampling or computing partial statistics in a distributed manner. If the data is labeled or partially labeled, external indices (like homogeneity, completeness, or V-measure) can be computed on a subset of points to approximate overall clustering performance.
Could you mention any specific pitfalls to watch out for?
One pitfall is insufficient attention to data scaling or normalization. Features on very different scales can dominate distance calculations in k-Means. Another pitfall is ignoring outliers, which may skew centroids significantly if not handled properly. Also, if the dataset is extremely sparse (for instance, high-dimensional text data), memory usage can skyrocket when converting to dense representations. Efficient sparse data handling is critical in such scenarios.
Can you adapt the above methods to incorporate domain knowledge?
In some domains, it may be known that certain points must belong to the same cluster or different clusters. Constrained k-Means can incorporate such domain knowledge, but the algorithm might need to be adapted to handle large datasets. Partitioning the dataset in a domain-informed way before clustering is another possibility, using known group boundaries or hierarchical structures.
These considerations, combined with careful tuning of implementation details, can make k-Means feasible and effective even on massive datasets.