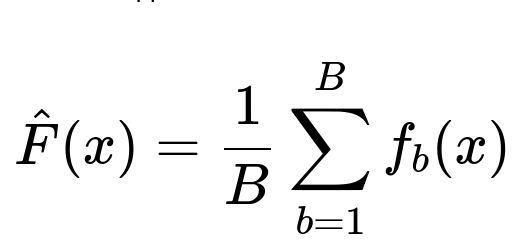ML Interview Q Series: How do Bagging methods differ from Boosting methods in ensemble learning?
📚 Browse the full ML Interview series here.
Comprehensive Explanation
Bagging and Boosting are two popular ensemble learning techniques that combine multiple weak learners to form a more robust predictive model. Although they share the same high-level objective of reducing generalization error, they differ significantly in how the ensemble is constructed and how each learner contributes to the final prediction.
Bagging (Bootstrap Aggregation)
Bagging typically aims to reduce variance by training multiple base learners on different bootstrap samples of the original dataset. Each base learner is trained independently in parallel. After training, their outputs are averaged (for regression) or voted upon (for classification). This often stabilizes the final prediction and mitigates overfitting.
When combining the predictions of multiple base learners in Bagging for regression tasks, a common approach is:
Here, B is the total number of base learners, and f_b(x) is the prediction of the b-th base learner for input x. Since all learners are equally weighted, the final prediction is the simple average of their outputs.
Typical use cases for Bagging: • Situations with high variance models (e.g., decision trees). • When parallel training is feasible. • Models susceptible to overfitting but with relatively small bias.
Boosting
Boosting focuses on reducing bias by training base learners iteratively. Each new learner attempts to correct the errors made by the previous ensemble. The idea is to assign higher weights (or emphasis) to the instances that were misclassified or had large residuals so that subsequent learners pay more attention to these difficult observations.
In a typical boosting framework (like Gradient Boosting for regression), the ensemble is formed by adding new models to the existing set of learners, gradually improving the overall performance:
Here, F_m(x) is the boosted model after the m-th iteration, F_{m-1}(x) is the model after (m-1) iterations, h_m(x) is the new weak learner, and nu is the learning rate (a small value controlling the contribution of each new learner). The learners are trained sequentially, and each new learner tries to address the shortfalls (residual errors) of the ensemble built up to that point.
Typical use cases for Boosting: • Problems where reducing bias is crucial (e.g., shallow trees or weak learners). • Datasets that allow sequential reweighting or residual correction. • Settings where iterative training is not prohibitively expensive.
Key Differences
• Training Strategy: Bagging trains each learner independently in parallel; Boosting trains them sequentially, with each learner focusing on previous errors. • Goal: Bagging reduces variance primarily; Boosting reduces bias. • Model Combination: Bagging typically averages (for regression) or majority-votes (for classification). Boosting usually produces a weighted sum of weak learners’ predictions. • Data Sampling: Bagging typically samples with replacement (bootstrapping) for each learner. Boosting reweights or shifts focus to misclassified/residual examples. • Risk of Overfitting: Bagging has a lower tendency to overfit as it stabilizes high-variance models. Boosting can overfit if the number of iterations is very large or if the weak learners fit noise too closely, though methods like early stopping and small learning rate can mitigate this.
Potential Follow-up Questions
Could you explain why bagging reduces variance but may not significantly reduce bias?
Bagging trains multiple high-variance base learners on bootstrapped samples. Because each base learner captures different subsets of the data, many of the idiosyncrasies they learn do not overlap. When these models are averaged, their individual variations partially cancel out, thus reducing variance overall. However, if each base learner is biased (for example, an underfitted model) or systematically incorrect in certain regions, simply averaging them may not drastically reduce that bias, because each learner is likely capturing the same inherent bias from the data or from the algorithm’s functional form.
When might boosting become prone to overfitting, and how do we mitigate it?
Boosting can be prone to overfitting if: • It runs for too many iterations, causing the ensemble to model noise in the data. • The base learners are too complex, allowing them to overfit local noise.
To mitigate these issues: • Use a small learning rate (nu) so that each learner contributes gradually and prevents drastic over-corrections. • Limit the depth or complexity of the weak learners to prevent them from fitting noise. • Employ early stopping, where you monitor performance on a validation set and stop boosting when performance ceases to improve or starts to deteriorate.
Why is random forest considered a bagging method, while gradient boosting is a boosting method?
Random Forest takes multiple decision trees and trains each one on a different bootstrap sample of the original dataset. The final prediction is the average (for regression) or majority vote (for classification) of these trees. This parallel, independent training of models on bootstrapped data aligns with the principles of Bagging.
Gradient Boosting sequentially builds models, each one attempting to correct the residuals of the ensemble so far. This iterative improvement, where each new model is added based on the shortcomings of the previous ones, characterizes Boosting.
How does parallelization differ between bagging and boosting?
In bagging, the base learners are trained independently, allowing for easy parallelization because each learner does not need to wait for the others’ results. In boosting, however, the training is sequential: each new learner depends on information from the previous learners (misclassified samples or residuals). This dependency chain makes parallelization more challenging, though certain parallel strategies can be employed inside each iteration.
Is there a scenario where bagging might outperform boosting despite boosting typically reducing bias more effectively?
Yes. In situations with very noisy data, boosting might chase noise and lead to overfitting if not properly regularized or if allowed to iterate excessively. Bagging (especially something like Random Forest) might perform better because it stabilizes predictions through averaging and does not iteratively focus on difficult points that might be noisy. Moreover, bagging can be more robust when you have a large dataset with high variance and want fast parallel solutions.
Could you describe the role of the learning rate in boosting?
The learning rate (often denoted as nu) is a small scalar that controls how strongly each new weak learner influences the ensemble. By multiplying the new weak learner’s predictions by nu before adding them to the ensemble, we ensure that each step is more conservative and avoids over-correcting for previous errors. This gradual building of the model generally leads to better generalization. A smaller learning rate requires more boosting iterations to converge, but it often yields better performance.
How do you choose the number of base learners in bagging and boosting?
In bagging: • You often train a large number of base learners (e.g., hundreds of decision trees in a Random Forest). After a certain point, adding more trees has diminishing returns but rarely harms performance significantly.
In boosting: • You must be more careful. Too few iterations might underfit, while too many might overfit. Typically, you use cross-validation or a validation set to monitor performance and choose a suitable stopping point. Early stopping techniques can help automate this process.
Would you use the same kind of weak learner for bagging and boosting?
Yes, it is common to use decision trees as the weak learner for both bagging and boosting. However, the parameter settings may differ. For bagging (like Random Forest), each tree can be fairly deep because the aim is to reduce variance via averaging. For boosting (like Gradient Boosted Decision Trees), the trees are often kept shallow (like depth 3–6) to focus on reducing bias step by step without overfitting too quickly. In principle, any classifier/regressor can be used as a weak learner for both methods, but trees are popular for their interpretability and performance.
Could boosting be useful for high-dimensional, sparse feature spaces?
Yes. Many boosting frameworks (like Gradient Boosting or XGBoost) handle high-dimensional, sparse data by performing efficient feature selection and splitting. The iterative nature of boosting can help to pinpoint important features that consistently reduce the loss in each round, even when the feature space is large. With proper regularization (e.g., shrinkage, column subsampling, or L1/L2 penalties), boosting can be quite effective in high-dimensional scenarios.
How does feature sampling in Random Forest relate to bias and variance?
Random Forest does not only sample data points but also samples a subset of features for splitting at each node. This reduces the correlation among trees, further decreasing variance because each tree is forced to consider potentially different feature subsets. It might slightly increase the bias (since some relevant features might be excluded in certain splits), but in practice, the overall effect on performance is usually beneficial, and the variance reduction often outweighs the possible increase in bias.
Why do we sometimes use more advanced loss functions in boosting rather than a simple mean squared error or cross-entropy?
Boosting methods like Gradient Boosting can optimize arbitrary differentiable loss functions. By choosing a loss function that aligns well with the problem (for instance, quantile loss for percentile estimates, or specialized losses for ranking tasks), you make the model better suited to capture the nuances of the specific objective. This can lead to improved performance compared to standard losses like mean squared error, especially in tasks with asymmetric error distributions or custom performance metrics.
Why do deeper trees in boosting risk overfitting more than in bagging?
In boosting, the model is built in stages: each tree corrects the residuals of the ensemble so far. If these trees are deep and highly expressive, they might be able to perfectly fit or come close to perfectly fitting the residuals—even if those residuals are noisy. This sequential fitting can quickly lead to overfitting. In bagging, deep trees independently fit their respective samples. Averaging over many such trees smooths out individual overfits, so deeper trees can still generalize well in a bagging context.
How do you handle class imbalance in bagging or boosting?
In bagging, you might: • Upsample minority classes or downsample majority classes in each bootstrap sample. • Adjust class weights so that misclassifying minority classes incurs a higher penalty.
In boosting, you could: • Modify the loss function to weight misclassified minority classes more heavily. • Incorporate specialized sampling strategies or adapt the reweighting scheme to focus on the minority class.
Both methods can be adapted to emphasize or penalize errors on the minority class, improving performance under imbalanced conditions.
How can we decide whether to use bagging or boosting for a particular problem?
Practical considerations include: • If you suspect the model suffers from high variance, bagging (e.g., Random Forest) can be a good starting point. • If you need to systematically reduce bias and have enough training data to avoid overfitting, boosting (e.g., Gradient Boosting) is often preferred. • If you have large-scale data and want parallelizable solutions quickly, bagging is typically simpler to deploy. • If you can invest time in tuning hyperparameters and carefully controlling overfitting, boosting methods often achieve superior performance.
You may also empirically evaluate both approaches via cross-validation and pick the one that yields better results given the constraints of your application.
Below are additional follow-up questions
How does hyper-parameter tuning differ between bagging and boosting?
In bagging methods (like Random Forest), the primary hyper-parameters typically include the number of estimators (trees), the maximum depth of each tree, and the number of features considered for splitting at each node. Tuning these mostly impacts how much variance is reduced and how correlated the individual learners are:
• Increasing the number of estimators often reduces variance but comes with diminishing returns after some point. • Adjusting maximum depth controls how complex each base learner can get—deeper trees can capture more complexity but might overfit. • Reducing the number of features considered at each split (e.g., sqrt of total features) further de-correlates the trees, usually reducing variance but potentially increasing bias slightly.
In boosting (like Gradient Boosting, XGBoost, or LightGBM), the hyper-parameters are more involved and can drastically affect both bias and variance:
• The number of boosting rounds (or estimators) determines how many times you iteratively improve the model. Too few may underfit; too many may overfit. • The learning rate (shrinkage parameter) scales the contribution of each weak learner and has a major influence on how quickly the model fits residuals. A smaller learning rate generally leads to better generalization but requires more rounds. • The maximum depth of each tree (if trees are used as weak learners) determines how flexible each learner is in capturing complex patterns. Deeper trees might reduce bias but risk higher variance and overfitting. • Sub-sampling of data or features (column subsampling) can be used to reduce correlation among the trees and improve generalization.
In practice, tuning boosting models is more nuanced because multiple interacting parameters (learning rate, number of estimators, tree depth, etc.) need to be balanced carefully. Bagging methods, while they do have multiple parameters, often require fewer delicate trade-offs and are simpler to tune.
Does the order of data processing matter for bagging and boosting?
In bagging, the order in which you feed data to each learner is largely irrelevant. Each base learner is trained independently on its own bootstrap sample. Whether you shuffle the data first or not, every learner obtains a random sample (with replacement) from the entire dataset.
In boosting, especially online or sequential variants, the order can matter if you implement a streaming-based booster that updates its model sequentially based on the incoming data. In most implementations (like standard XGBoost), the data is still randomly shuffled or fixed in memory, and you train multiple passes over the same dataset. However, in an online boosting scenario where models are updated in real time, the data order could impact how the weights or residuals are updated, potentially leading to different results. This is generally considered a more specialized situation. In batch mode boosting, data order does not matter because all of the data is available upfront.
How can we extend bagging and boosting to multi-class or multi-output problems?
Bagging and boosting approaches naturally generalize to multi-class classification and multi-output tasks with some adjustments:
• For bagging: – In classification, each base learner can be trained on the multi-class problem, and the final prediction is often determined by a majority vote among the learners. – For multi-output regression, each learner produces multiple outputs (one per target dimension), and the predictions are averaged across learners for each output dimension.
• For boosting: – For multi-class problems, boosting frameworks typically use a multi-class loss function (e.g., softmax cross-entropy). The sequential training approach is applied to each class’s predicted probabilities or logits, and each iteration tries to reduce the multi-class loss for the current ensemble. – In multi-output regression, each tree can produce multiple outputs (one per dimension of the target), or the algorithm can train separate trees for each output dimension, depending on the implementation.
The main complexity lies in defining an appropriate loss function and ensuring the iterative updates (in boosting) handle multiple classes or outputs correctly. Most modern libraries offer built-in support for multi-class and multi-output tasks, making the extension straightforward from a user perspective.
Are there theoretical guarantees or known limitations for bagging and boosting?
Bagging
• Theoretical Guarantee: Under certain assumptions, bagging reduces variance by averaging uncorrelated estimators, which can lead to a better expected performance compared to a single estimator, especially if the individual estimators are high variance. • Limitation: If each estimator has a significant bias, simply averaging them won’t effectively reduce that bias. Also, bagging might not lead to substantial improvements if the base learners are already low-variance or if they are highly correlated.
Boosting
• Theoretical Guarantee: Gradient boosting can be viewed as a gradient descent procedure in function space, providing a solid foundation from an optimization perspective. With a convex loss, boosting converges to a minimum as more weak learners are added, provided the learning rate is sufficiently small. • Limitation: Boosting can overfit if it is not carefully regularized, especially when dealing with noisy data or when using highly flexible base learners. Additionally, for very large datasets, sequential boosting can be computationally more intensive than bagging unless parallelized implementations are used.
What if we apply bagging to shallow trees or apply boosting to deep trees?
• Bagging shallow trees: Shallow (e.g., depth-1 or depth-2) trees have lower variance but higher bias. Bagging a large ensemble of shallow trees may not reduce the bias enough to improve performance significantly, although it will likely be robust to overfitting. This is sometimes done if computational resources are limited or if interpretability is required. However, random forests typically use deeper trees to maximize the variance reduction effect.
• Boosting deep trees: Deeper trees can capture complex patterns and potentially reduce bias faster. However, each new tree in boosting focuses on the residuals of the previous stage, so a deep tree can quickly overfit these residuals, leading to high variance. You can mitigate this by using a smaller learning rate, adding regularization like subsampling or column sampling, or imposing constraints (like limiting leaf weights).
How can we evaluate performance improvements and are there specific metrics to consider for bagging vs. boosting?
Performance for both methods is generally compared to a baseline single model, using metrics such as accuracy, precision, recall, F1-score (classification) or mean squared error, mean absolute error, R^2 (regression). You may also look at:
• Stability of predictions: Bagging typically stabilizes predictions as it reduces variance, so you might measure performance variance across multiple cross-validation folds or repeated runs to see how stable the result is. • Learning curves: For boosting, plot training and validation error vs. number of estimators (boosting rounds) to see if the model is overfitting or underfitting. • Feature importances: Both bagging and boosting can provide feature importances for tree-based ensembles. However, the distribution and magnitude of these importance scores may differ; in boosting, certain features that help reduce residuals might appear more critical.
No special metric is exclusively for bagging or boosting, but certain ensembles might exhibit different biases (e.g., if boosting overfits, you could see a sudden divergence in validation metrics).
How does cross-validation integrate with bagging and boosting, and can we reuse any partial results?
Bagging
You normally perform cross-validation by repeatedly training the entire bagged ensemble on each fold of the data. Because each fold is a completely separate training run, you typically cannot reuse the models from other folds (they are trained on different subsets of the data). Random forests, for instance, are quite fast to train in parallel, so retraining for each fold is often acceptable.
Boosting
Similarly, each fold requires you to start the boosting process anew. If you’re training many rounds (hundreds or thousands of estimators), this can be computationally heavy. Some libraries enable approximate reuse of partially trained models (e.g., warm start) to skip reinitializing from scratch, but caution is needed because each fold uses a different training subset. Data leakage or incorrect handling of folds can happen if you try to reuse partial models without carefully ensuring the training data distribution is consistent.
Do bagging or boosting always improve performance over a single model? Under what circumstances might they degrade performance?
Potential Gains
• When base learners have high variance, bagging shines by averaging out spurious fluctuations. • When base learners have high bias (and the residuals are learnable), boosting can systematically reduce that bias.
Possible Degradation
• If the data is extremely noisy or the model is too flexible, boosting can overfit and perform worse. • If base learners are already near-optimal or have low variance, bagging may not yield big improvements and can add unnecessary complexity. • If hyper-parameters (like learning rate, tree depth, or number of estimators) are not tuned properly, you might end up with a suboptimal ensemble.
In real-world practice, you must validate the ensemble on a held-out set or via cross-validation to ensure that ensemble methods are indeed providing a benefit.
How do computational cost and memory usage differ between bagging and boosting in production systems?
Bagging
• Training: Each learner is trained independently and in parallel, which can be efficient if you have a multi-core or distributed environment. The complexity for training T trees each of maximum depth D is typically O(T * n * D) for many tree implementations, where n is the dataset size. • Memory: You need to store T separate models. For decision trees, each tree has its own nodes, but memory usage scales linearly with T.
Boosting
• Training: Boosting is sequential. Though modern libraries do partial parallelization within each iteration (for example, building individual splits in parallel), you cannot fully parallelize the entire process as easily as bagging. The complexity for T boosters is also roughly O(T * n * D), but each iteration depends on the residuals or gradients from the previous step. • Memory: You store T trees, similar to bagging, but might also store additional structures (e.g., gradient statistics). Advanced implementations like XGBoost compress trees in memory, but in large-scale scenarios, it can still be memory-intensive.
In production, both methods can be made efficient, but bagging often has an edge if large-scale parallel resources are available, while boosting might require more careful engineering to achieve the same level of distributed performance.
How do these methods scale in a distributed environment or for massive datasets?
• Bagging: Highly amenable to distributed and parallel computing. You can split data across different machines, train separate models independently, and then aggregate their predictions. This approach is straightforward and widely used for large-scale data processing frameworks like Spark. • Boosting: More challenging because of the sequential nature. However, implementations like XGBoost or LightGBM incorporate distributed training by partitioning data across workers and merging gradient statistics. The biggest bottleneck is synchronizing these statistics at each boosting round. With well-engineered libraries, boosting can still scale to very large datasets, but it typically requires more sophisticated infrastructure and care in partitioning data, especially if communication overhead is high.
Potential pitfalls include: • Network bottlenecks when passing residual or gradient information among workers. • Imbalanced data distribution across partitions leading to poor gradient estimates or skewed splits.