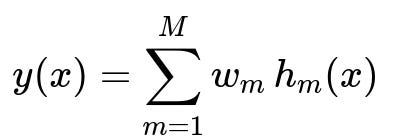ML Interview Q Series: How do ensemble-based methods support incremental learning over time?

📚 Browse the full ML Interview series here.

Comprehensive Explanation

Ensemble techniques can be very advantageous in incremental learning scenarios, where data arrives in batches or streams. In incremental learning, the model is continuously updated to incorporate new information without having to retrain from scratch. Ensembles bring diversity of predictions, enabling better generalization and greater adaptability.

Core Idea of Ensemble Learning

Ensemble learning combines multiple base learners to produce a final prediction. Each base learner can be trained on different subsets of data or can be slightly varied in terms of hyperparameters or architectures. The goal is to mitigate the risk of overfitting to a single hypothesis and to reduce variance or bias, depending on the ensemble method (e.g., Bagging reduces variance, Boosting reduces bias).

Incremental Learning Challenges

Incremental learning usually faces several key issues:

• The potential for catastrophic forgetting, where the model fails to retain previously learned knowledge when updated with new data.

• Memory constraints, because storing all historical data for retraining is not always feasible.

• Shifting data distributions (concept drift), where new data can differ significantly from previous patterns.

How Ensembles Address Incremental Learning

Adaptive Updating of Base Learners When new data arrives, each base learner in the ensemble can be updated independently (assuming each learner supports partial or online updates). This ensures that the ensemble collectively reflects the latest data without forgetting earlier patterns completely, since each base learner may capture a different slice or aspect of the data distribution.

Model Replacement / Windowing In scenarios with a strict memory or computational budget, instead of updating all existing base learners, one might periodically replace the oldest or weakest base learner with a newly trained one on the latest data. This is particularly helpful if the distribution shifts significantly over time.

Reduced Catastrophic Forgetting Since each member of the ensemble retains knowledge gained from different data segments (or different time steps), the entire ensemble is less prone to forgetting earlier patterns. Aggregating predictions from multiple learners preserves the overall knowledge base.

Online Boosting / Streaming Ensembles There are specialized variants of boosting and bagging adapted for streaming data. These methods incrementally update weights for each base learner or add new learners as data streams in. This focuses the ensemble’s attention on new data without discarding earlier insights.

Mathematical Perspective

When discussing the combination of an ensemble’s base learners, a common approach is to sum or average the outputs of individual models, possibly with different weights. A typical formulation for an ensemble’s final output y(x) for a regression or classification (before a decision function like argmax for classification) is shown below:

Here, M is the number of base learners in the ensemble, h_m(x) is the prediction of the m-th base learner, and w_m is the weight assigned to that base learner. In incremental learning:

• h_m(x) could be a model that is updated or retrained partially on incoming data.

• w_m might be recalculated over time to emphasize newer or more accurate learners if the data distribution shifts.

Example Code in Python

Below is a simple conceptual illustration using scikit-learn-like partial_fit for incremental learning. We assume each base learner supports the partial_fit method (e.g., SGDClassifier, Perceptron, or MultinomialNB).

import numpy as np
from sklearn.linear_model import SGDClassifier
from sklearn.naive_bayes import MultinomialNB

class IncrementalEnsemble:
    def __init__(self, models, weights=None):
        # models is a list of incremental learners
        self.models = models
        if weights is None:
            self.weights = np.ones(len(models)) / len(models)
        else:
            self.weights = np.array(weights)

    def partial_fit(self, X, y, classes=None):
        for model in self.models:
            model.partial_fit(X, y, classes=classes)

    def predict(self, X):
        # Summation of weighted predictions (for classification, argmax over class probabilities)
        predictions = []
        for model, w in zip(self.models, self.weights):
            predictions.append(w * model.predict_proba(X))
        ensemble_output = np.sum(predictions, axis=0)
        return np.argmax(ensemble_output, axis=1)

# Example usage:
X_initial = np.random.rand(100, 20)
y_initial = np.random.randint(0, 2, 100)

model1 = SGDClassifier(loss="log")
model2 = MultinomialNB()

# Initialize them with a small batch
model1.partial_fit(X_initial, y_initial, classes=[0, 1])
model2.partial_fit(X_initial, y_initial, classes=[0, 1])

ensemble = IncrementalEnsemble([model1, model2], weights=[0.5, 0.5])

# Stream in new data
X_new = np.random.rand(50, 20)
y_new = np.random.randint(0, 2, 50)

# Incrementally update
ensemble.partial_fit(X_new, y_new, classes=[0,1])

# Prediction on test
X_test = np.random.rand(10, 20)
y_pred = ensemble.predict(X_test)

In this conceptual example, each base learner is incrementally updated with the partial_fit method whenever new data arrives, and the ensemble aggregates their outputs.

Potential Follow-up Questions

Could you elaborate on how an ensemble mitigates catastrophic forgetting more effectively than a single model?

When a single model is incrementally trained, it updates its parameters based on incoming data. If the model structure does not explicitly preserve older information, it might overwrite learned parameters to accommodate new patterns (catastrophic forgetting). An ensemble, on the other hand, can maintain multiple base learners, each potentially trained on or updated with different segments of the data over time. By combining them, the final prediction is less likely to discard older knowledge altogether.

Additionally, ensembles can adopt strategies such as:

• Keeping some base learners “frozen” once trained (ensuring historical knowledge is preserved).

• Employing weighted updates so that older models still influence the final output unless it becomes clear their knowledge is no longer relevant.

How do we handle concept drift in incremental learning with ensembles?

Concept drift means the statistical properties of the target variable and features change over time. With ensembles, one approach is to rotate out older models that have become obsolete if the data distribution changes significantly. A window-based strategy can be used: the system trains a new model on the latest data window and discards the oldest model, thus ensuring the ensemble is aligned with recent patterns.

For abrupt concept drift, you might decrease the influence of older learners (by lowering their weights). For gradual drift, you may slowly shift the balance between older and newer models. There are also drift detection mechanisms (e.g., monitoring the error rates) that trigger the creation of new models or the removal of outdated ones.

Is it always beneficial to use ensembles for incremental learning?

Not always. While ensembles can improve robustness and predictive performance, they also:

• Require more memory and computational resources because multiple models must be maintained.

• May need additional careful tuning of ensemble size and weighting mechanisms.

• Can be harder to interpret compared to a single incremental model.

In highly constrained environments, a single incremental model might be sufficient and simpler to maintain. Still, in many real-world data stream situations, the performance gains of ensembles can outweigh these costs.

How can we ensure that older patterns don’t overly dominate if the data distribution changes drastically?

When the data distribution changes significantly, older models may no longer be relevant. To handle this, one might:

• Decrease the weights of base learners that perform poorly on the new data.

• Remove or replace outdated models entirely.

• Use explicit drift detection algorithms that signal when it is time to retrain models from scratch or remove them.

This ensures that the ensemble remains an accurate reflection of the present data distribution rather than clinging to obsolete historical patterns.