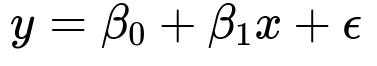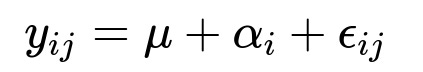ML Interview Q Series: How do regression-based models differ from ANOVA in a statistical framework?
📚 Browse the full ML Interview series here.
Comprehensive Explanation
Regression models and ANOVA (Analysis of Variance) models are both used to explain variations in a response variable, often under the umbrella of the general linear model framework. However, they differ in the way predictors (i.e., independent variables) enter the model and in how one typically interprets the results.
Conceptual Comparison
A regression model commonly uses continuous predictors, although it can also accommodate categorical factors by coding them into dummy (indicator) variables. ANOVA, on the other hand, primarily focuses on comparing mean responses across different groups or levels of categorical factors.
But in truth, an ANOVA model can be seen as a special case of a linear regression model where the predictors are purely categorical. In classical ANOVA settings, the primary interest is in whether there is a statistically significant difference among the means of multiple groups, whereas in standard regression settings, the typical goal is to understand how changes in a continuous or coded-predictor variable affect the response.
Mathematical Formulations
Linear Regression Model
A standard linear regression with one predictor can be written as:
Here, y is the response variable, x is a continuous predictor, beta_0 is the intercept, beta_1 is the slope coefficient, and epsilon is the error term that captures unexplained variation.
When there are multiple continuous predictors, you might have additional terms beta_2 x_2, beta_3 x_3, and so on. For categorical variables, you introduce dummy variables to represent each factor level (except a baseline). The regression approach then estimates a coefficient for each dummy variable, reflecting how each category’s mean differs from the baseline.
One-Way ANOVA Model
A one-way ANOVA with k groups can be expressed as:
where y_{ij} is the response of the jth observation in the ith group, mu is the overall mean, alpha_i is the effect (or deviation from mu) for the ith group, and epsilon_{ij} is the error term. Typically, we impose a constraint (such as sum of alpha_i across i=1..k is zero) to ensure identifiability. This model focuses on determining whether at least one alpha_i differs significantly from zero, implying differences among group means.
Interpretation and Use Cases
In a regression setting, you interpret each coefficient as the change in the response variable corresponding to a unit change (or specified contrast) in the predictor variable, assuming all other predictors remain fixed. You can incorporate many continuous predictors, and you can also add categorical variables by means of dummy encoding.
In an ANOVA setting, you are testing whether group means differ. Specifically, you often look at the overall F-test to see whether there is a difference among any of the means. Post-hoc comparisons (such as Tukey’s HSD, Bonferroni, or similar methods) help identify which group means differ.
Typical Assumptions
Both regression and ANOVA models share similar assumptions:
Normality: The residuals for each level of the predictor(s) (or each group in ANOVA) are normally distributed.
Homoscedasticity: The variance of the residuals is constant across different levels of the predictor(s) or groups.
Independence: The data points (observations) are independently sampled.
In regression, you often check for linearity of the relationship (between predictors and the response) as an additional assumption or modeling choice. For ANOVA, you focus on verifying that the data distribution in each group meets the normality and equal variance requirements.
Combined View (ANOVA as a Special Case of Regression)
It is critical to see that ANOVA is essentially a regression model with purely categorical predictors. If you use dummy variables to indicate group membership, the model effectively replicates an ANOVA. This viewpoint is extremely powerful, because it allows more flexible modeling (e.g., ANCOVA) where you have both continuous and categorical predictors in the same model.
Practical Scenarios
If you have one or more continuous predictors and you want to quantify how they affect a continuous response, you will typically use linear regression.
If your primary interest is checking whether different groups (e.g., treatment groups) yield different mean outcomes, then a straightforward one-way ANOVA or multi-factor ANOVA is common.
Potential Follow-Up Questions
Can we treat ANOVA and Regression as fundamentally the same technique?
They are closely related under the general linear model framework, but in practice, we label it “ANOVA” when the focus is purely on differences among group means (categorical factors). We call it “regression” when interest is in quantifying the effect of continuous and/or dummy-coded predictors. From a mathematical standpoint, an ANOVA model can indeed be seen as a special case of a regression model. However, the nomenclature and typical interpretations differ, especially concerning how results are reported and interpreted.
What happens if you include both continuous and categorical predictors together?
If you mix continuous and categorical predictors in a model, you essentially have an ANCOVA (Analysis of Covariance). Conceptually, it combines ANOVA’s focus on group-level differences with regression’s continuous covariates. In practice, you include dummy variables to represent the categorical factors and standard numeric columns for the continuous covariates. The model then estimates how group means differ after adjusting for the continuous variables.
How does interpretability change when we code categorical variables in regression?
When using dummy variables, one of the categories is chosen as a reference (baseline). The coefficients associated with the dummy variables then indicate how the mean of the response differs for each category relative to that baseline category. This approach remains intuitive but can sometimes become more complex to interpret if there are many categories or if you include interactions between categorical and continuous variables.
How do we check the assumptions for ANOVA or Regression?
For both:
Generate residual plots to examine whether variance appears constant (homoscedasticity).
Check normality of residuals via histograms or Q-Q plots.
Look for outliers or influential points using diagnostic plots (e.g., Cook’s distance). In ANOVA, you should also verify that each group’s residuals meet the assumption of normality, and that variances across groups are relatively equal. In regression, you often focus on residual vs. fitted plots to assess homoscedasticity and linearity assumptions.
What are common pitfalls in using ANOVA vs. Regression?
One frequent mistake is assuming that ANOVA cannot handle covariates. ANOVA is not limited to purely categorical designs; you can extend to ANCOVA. Another pitfall is misinterpreting the effect of dummy variables or incorrectly specifying the baseline category in regression. Finally, an important pitfall in ANOVA is forgetting to conduct post-hoc comparisons after discovering a significant overall F-test. Failing to do so leaves you uncertain which group pairs actually differ.
Can you give a quick Python snippet showing how one might run a regression for a categorical predictor vs. an ANOVA approach?
import pandas as pd
import statsmodels.api as sm
import statsmodels.formula.api as smf
# Suppose we have a dataset with a categorical variable "group" and a response variable "y"
# Data as a dataframe
data = pd.DataFrame({
'group': ['A', 'A', 'B', 'B', 'C', 'C', 'A', 'B', 'C'],
'y': [5.1, 6.3, 7.2, 7.0, 6.8, 6.9, 5.4, 7.5, 7.0]
})
# Regression approach with dummy coding
model_reg = smf.ols('y ~ C(group)', data=data).fit()
print("Regression summary:")
print(model_reg.summary())
# ANOVA approach
anova_table = sm.stats.anova_lm(model_reg, typ=2)
print("\nANOVA table:")
print(anova_table)
In this example, C(group) treats “group” as a categorical variable in a regression formula context. The anova_lm function then displays the ANOVA-style table. Under the hood, both procedures rely on similar computations, illustrating how ANOVA is just a specialized regression for categorical predictors.