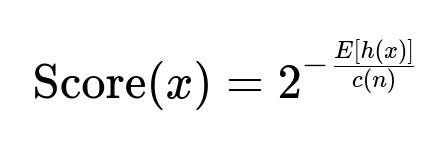ML Interview Q Series: How do we employ Isolation Forest for discovering anomalies in a dataset?

📚 Browse the full ML Interview series here.

Comprehensive Explanation

Isolation Forest is a model designed for outlier detection by capitalizing on the idea that anomalies are easier to isolate than normal instances. It splits the data space randomly and measures how quickly a point becomes isolated. Points requiring fewer splits to be isolated are more likely to be anomalies, while those needing more splits are likely normal.

The model creates multiple isolation trees, each one constructed from random splits on various features. For every new data point, the path length within each isolation tree is computed (the path length is the number of edges traversed from the root node to the terminal node). Averaging all the path lengths across the trees produces a measure indicative of how anomalous the point is: shorter path lengths indicate higher suspicion.

To measure anomalousness, a common scoring scheme compares the path length of a point to the average path length expected in a similarly sized random tree structure. If the observed path length is substantially shorter, that data point is likely an outlier.

Below is a formula often presented for the anomaly score. Let E[h(x)] be the mean path length over all the trees for a point x, and let c(n) be the average path length of a point in a binary tree built on n points.

In the above formula, E[h(x)] is the average path length of x across all isolation trees. Larger E[h(x)] implies x typically requires more splits to be isolated, indicating it is more normal. Smaller E[h(x)] implies x is easier to isolate, suggesting it may be an anomaly. The term c(n) is a normalizing factor to make the score consistent and comparable across different sample sizes.

The average path length c(n) of an unsuccessful search in a binary tree can be approximated as:

where H(n-1) is the (n-1)th harmonic number. This approximation helps adjust the expected path length when the dataset size changes.

When applying Isolation Forest in practice, we randomly sample subsets from the entire dataset to construct the forest. Each tree isolates points by choosing a feature at random and splitting it at a random threshold. Once the forest is built, each data point receives an anomaly score. By setting a threshold on this score, one can label points as anomalous or normal.

Below is a basic Python example using scikit-learn’s IsolationForest:

from sklearn.ensemble import IsolationForest
import numpy as np

# Example synthetic data
X = np.array([[1], [2], [2.5], [3], [100], [101], [3.5], [4], [5]])

# Instantiate and fit Isolation Forest
iso_forest = IsolationForest(n_estimators=100, contamination='auto', random_state=42)
iso_forest.fit(X)

# Predict anomaly scores
scores = iso_forest.score_samples(X)
# Higher scores indicate more "normal" points; lower scores indicate anomalies

# Predict outlier/normal labels (-1 = outlier, 1 = inlier)
labels = iso_forest.predict(X)

print("Anomaly scores:", scores)
print("Predicted labels:", labels)

In this code, IsolationForest is built with a certain number of estimators (n_estimators). The contamination parameter can be set to a specific value that reflects the expected proportion of outliers. Once fitted, score_samples gives the anomaly scores and predict yields a label for each point.

How does randomness in splits help capture anomalies?

Each isolation tree is built by randomly selecting a feature and a split point, which reduces bias toward particular directions of the dataset. By ensembling many such randomized trees, anomalies become consistently easier to isolate in multiple trees, resulting in a shorter average path length overall. This randomness makes the method robust to various data distributions and helps avoid overfitting.

What role does the contamination parameter play?

Isolation Forest requires an estimate (or an upper bound) of the expected fraction of anomalies in the dataset. If the user sets contamination too high, legitimate inliers may become flagged as outliers because the algorithm is forced to label a larger proportion of points as anomalies. Conversely, if it is set too low, genuine outliers might be overlooked.

How do we interpret the anomaly scores?

When you call score_samples, you receive values that correlate with normality—the higher the score, the more normal the instance. In many implementations, the scores are transformed so that large negative values indicate outliers. The threshold for deciding whether a point is an anomaly depends on the distribution of these scores and the user-defined contamination proportion.

Does Isolation Forest handle high-dimensional data effectively?

Isolation Forest can work in higher dimensions because it randomly chooses features to split. However, as dimension increases, random splits might become less meaningful in practice, especially if the data is sparse. It is wise to employ dimensionality reduction or feature selection when the dimensionality is very large, to help the model isolate anomalies more effectively.

What are potential pitfalls or limitations?

A key limitation is the challenge of choosing hyperparameters like the number of trees or the contamination factor without domain knowledge. Additionally, if the dataset is small or not well-represented, random splits may be noisy. In extremely high-dimensional spaces, random splits can struggle to delineate anomalies from normal points unless carefully tuned or combined with dimensionality reduction.

How do we use this approach in a streaming or changing environment?

In cases where data streams continuously or the underlying distribution shifts over time (concept drift), Isolation Forest might need to be retrained or updated periodically. One approach is to maintain a rolling window of the most recent data, discarding older points so the model always reflects the latest distribution. Alternatively, advanced streaming variants or incremental learning approaches can be used, but these are more specialized.

Why choose Isolation Forest over other anomaly detection methods?

It has appealing computational efficiency compared to some other outlier detection algorithms because it builds relatively shallow trees and does not require pairwise distance computations across the dataset. It also has a clear interpretability in terms of path lengths. That said, performance depends on how well the random splits isolate anomalies in a specific problem setting.

By constructing multiple trees to isolate data points, averaging their path lengths, and then using a threshold to label anomalies, Isolation Forest provides an efficient and robust mechanism to detect outliers in many real-world scenarios.